Структуры данных, которые мы использовали до сих пор имели фиксированный размер. В основном мы работали с одно- или двухмерными массивами. В этом разделе мы познакомимся с динамической структурой данных, называемой бинарным деревом. Бинарные деревья поиска (Binary Search Trees, или BST) являются одними из наиболее часто используемых типов структур данных. Они применяются при создании текстовых процессоров, компиляторов, операционных систем, графических систем, баз данных и других программных комплексов, в которых необходим быстрый доступ к хранимым элементам и простота в управлении динамикой структуры.
Динамические структуры данных (часто называемые коллекциями, или контейнерами) могут изменять свой размер во время исполнения. Они либо раздуваются (при добавлении элементов в коллекцию), либо сжимаются (при удалении). Они способны хранить объекты произвольного типа. Однако существуют и типизированные коллекции, настроенные на хранение данных одного, строго определенного типа. Напомним, какие типы динамических структур различают в дискретной математике.
¨ Векторы — это упорядоченные структуры (последовательности), которые работают по принципу резиновых массивов. В процессе своей работы они динамически резервируют и перераспределяют память.
¨ Связанные списки — это упорядоченные структуры, позволяющие легко вставлять и удалять элементы в произвольные позиции коллекции. Поиск в таких структурах не эффективен.
¨ Стеки часто используются редакторами текстов (для реализации операций Undo-Redo), компиляторами и операционными системами для запоминания и выборки параметров. Стеки позволяют вставлять и выбирать данные с одного конца коллекции—вершины стека.
¨ Очереди используются операционными системами для обработки событий. Программа поддержки устройства типа ATM-switch (переключателя маршрутов соединений) использует очереди для обработки ситуаций временного переполнения. Очереди поддерживают в коллекции дисциплину: первым вошел—первым вышел. Вставка данных производится с одного конца, а выбор—с другого.
¨ Ассоцативные массивы
¨ Бинарные деревья позволяют производить быстрый поиск, вставку данных в определенную позицию и вывод в отсортированном виде. Они используются при компиляции выражений машинных языков, в словарях и имеют ряд других интересных применений.
Списки, стеки и очереди являются линейными структурами (последовательностями). Деревья (в частном случае бинарные)—это нелинейные структуры, обладающие специальными свойствами.
Для описания принципа работы дерева используют понятие узла и ветви. Дерево состоит из элементов, называемых узлами. Часть дерева (поддерево), состоящая из связанного подмножества его узлов называют ветвью. Каждый узел бинарного дерева состоит из ссылки на какое-то информационное поле (объект данных, хранимых в дереве) и двух указателей на узлы дерева. Один из указателей ссылается на левую ветвь, другой — на правую. Схематически узел дерева часто обозначают так, как показано на рисунке справа.

В списках также используется понятие узла. Узел односвязного списка содержит ссылку на данные и указатель на следующий элемент.
Бинарное дерево, как и дерево в природе, начинается с корня. Абстрактному дереву корнем служит указатель на один из его элементов. Дерево упорядочивается по какому-либо информационному полю. Такое поле называется ключевым. В дереве могут быть узлы с одинаковым значением ключевого поля, но обычно такой сценарий исключается. Структура кроны дерева однозначно определяется порядком поступления ключевых полей при формировании дерева. Предположим, что узлы поступают на вход процедуры, формирующей дерево и первым приходит узел с ключом 16. Тогда дерево приобретет такой вид.

Предположим, что после узла 16 поступил узел с ключом 3. Он будет вставлен в левую ветвь предыдущего узла, так как 3 < 16.
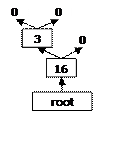
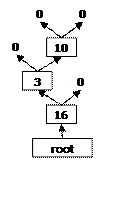
Поиск места прикрепления узла к дереву производится в соответствии с алгоритмом: если ключ вставляемого узла меньше ключа узла текущего, то текущим становится левый узел, иначе—правый. Это действие повторяется до тех пор, пока существует текущий узел. Если текущий узел найти не удается (ссылка на него равна нулю), то место прикрепления к дереву найдено. Предположим, что следущим приходит узел с ключом 10. Путь к месту вставки будет определяться шагами: влево, вправо, а дерево приобретет вид.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.