Розрахунок надійності елементів автоматизованих систем управління по контролю і обліку енергоносіїв офісних і житлових приміщень

5 РОЗРАХУНОК НАДІЙНОСТІ ЕЛЕМЕНТІВ АВТОМАТИЗОВАНИХ СИСТЕМ УПРАВЛІННЯ ПО КОНТРОЛЮ І ОБЛІКУ ЕНЕРГОНОСІЇВ ОФІСНИХ І ЖИТЛОВИХ ПРИМІЩЕНЬ

Найпростішим випадком в розрахунковому сенсі є послідовне з'єднання елементів системи. У такій системі відмова будь-якого елементу рівносильна відмові системи в цілому. По аналогії з ланцюжком послідовно сполучених провідників, обрив кожного з яких рівносильний розмиканню всього ланцюга, ми і називаємо таке з'єднання "послідовним" (мал. 5.1). Слід пояснити, що "послідовним" таке з'єднання елементів є тільки в сенсі надійності, фізично вони можуть бути сполучені як завгодно|.

Малюнок 5.1 – Блок-схема системи з послідовним з'єднанням| елементів

З позиції надійності, таке з'єднання означає, що відмова пристрою, що складається з цих елементів, відбувається при відмові елементу 1 або елементу 2, або елементу 3, або елементу n. Умову працездатності можна сформулювати таким чином: пристрій працездатний, якщо працездатний елемент 1 і елемент 2, і елемент 3, і елемент n.

Виразимо надійність даної системи через надійності її елементів. Нехай є деякий проміжок часу (0,t), протягом якого потрібно забезпечити безвідмовну роботу системи. Тоді, якщо надійність системи характеризується законом надійності Р(t), нам важливо знати значення цієї надійності при t=t, тобто Р(t). Це не функція, а певне число; відкинемо аргумент t і позначимо надійність системи просто Р. Аналогічно позначимо надійності окремих елементів р₁, р₂, р₃ ..., р_n.

Для безвідмовної роботи простій системи протягом часу t потрібно, щоб безвідмовно працював кожен з її елементів. Позначимо S - подія, що полягає в безвідмовній роботі системи за час t; s₁, s₂, s₃ ..., s_n - події, що полягають в безвідмовній роботі відповідних елементів. Подія S є добуток (поєднання) подій s₁, s₂, s₃ ..., s_n: S = s₁·s₂·s₃·...s_n.

Припустимо, що елементи s₁, s₂, s₃ ..., s_n відмовляють незалежно один від одного (або, як говорять стосовно надійності, "незалежні по відмовах", а зовсім стисло "незалежні"). Тоді за правилом множення вірогідності для незалежних подій Р(S)=P(s₁)×P(s₂)×P(s₃)×...P(sn|) або в інших позначеннях

Р = р₁×р₂×р₃×...×р_n.,                                                  (5.1)

або

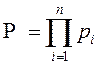                                                              (5.2)

Тобто надійність (вірогідність|ймовірність| працездатного стану|достатку|) простій системи, складеної з|із| незалежних по відмовах, послідовно сполучених|з'єднаних| елементів, рівна твору|добутку| надежностей| її елементів.

У окремому випадку, коли всі елементи володіють однаковою надійністю р1=р2=р3=| ... =р_n, вираз|вираження| (5.2) приймає вигляд|вид|:

Р = рn|.        (5.3)

Інтенсивність відмов системи при експоненціальному законі розподілу часу повністю легко визначити з|із| виразу|вираження|:

          (5.4)

Тобто|цебто| як суму інтенсивностей відмов незалежних елементів. Це і природно, оскільки|тому що| для системи, в якій елементи сполучені|з'єднані| послідовно, відмова елементу рівносильна відмові системи, означає|значить| всі потоки відмов окремих елементів складаються в один потік відмов системи з|із| інтенсивністю, рівній сумі інтенсивностей окремих потоків.

Формула (5.4) виходить з|із| виразу|вираження|:

Р = р1| Oр2| Oр3| O... Oрn| = ехр|{-()}.                  (5.5)

Середній час роботи повністю:

Т0 = 1/лс.    (5.6)

На мал. 5.2 представлено|уявляти| паралельне з'єднання|сполучення,сполуку| елементів 1, 2, 3. Це означає, що пристрій|устрій|, що складається з цих елементів, переходить в стан|достаток| відмови після|потім| відмови всіх елементів за умови, що|при умові , що,при условии | всі елементи системи знаходяться|перебувають| під навантаженням, а відмови елементів статистично незалежні.

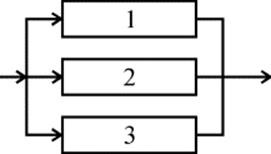
Малюнок 3.2 – Блок-схема системи з|із| паралельним з'єднанням|сполученням,сполукою| елементів

Інтенсивність відмов пристрою|устрою| що складається з n паралельно сполучених|з'єднаних| елементів, що володіють постійною інтенсивністю відмов л0|, визначається як:

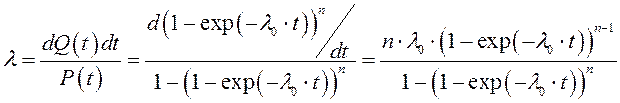.                                                                                                                     (5.7)

З|із| (5.7) видно|показний|, що інтенсивність відмов пристрою|устрою| при n >1 залежить від t: при t=0| вона рівна нулю|нуль-індикатору,нуль-множині,нуль-последовності,нуль-елементу|, при збільшенні t, монотонно зростає до л0|.