ПРИЛОЖЕНИЕ
РЕШЕНИЕ ДВУХТОЧЕЧНЫХ КРАЕВЫХ ЗАДАЧ МЕТОДОМ ИНВАРИАНТНОГО ПОГРУЖЕНИЯ
Инвариантное погружение возникло как обобщение принципов инвариантности, введенных В. А. Амбарцумяном [72]. Основная идея инвариантного погружения состоит во включении частной задачи в более общую. Часто решение общей задачи получить легче, чем решение частной. Если можно решить общую задачу, то частная задача решается автоматически. Инвариантное погружение применялось в различных областях.
Р. Беллман, Р. Калаба и другие исследователи [57]-[59] применили теорию инвариантного погружения для преобразования
линейных двухточечных краевых задач, возникающих в задачах оптимального
управления, в задачу Коши. Э. Сейдж и Д. Мелса [59] распространили этот
подход для преобразования нелинейной двухточечной краевой задачи, возникающей в
задачах нелинейной фильтрации, в задачу Коши. Задачу нелинейной фильтрации они
рассматривали как задачу оптимального управления нелинейным объектом, которая
заключается в определении оптимального управляющего воздействия ![]() путем минимизации квадратичной целевой
функции
путем минимизации квадратичной целевой
функции
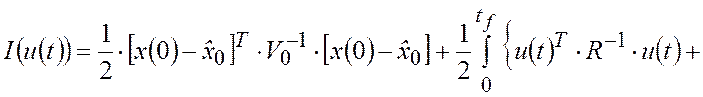
|
|
(П.1) |
при ограничении
|
|
(П.2) |
![]() ;
;
![]() – вектор погрешностей измерений.
– вектор погрешностей измерений.
Задача минимизации целевой функции (П.1) при ограничении (П.2) представляет собой частный случай задачи оптимального управления нелинейным динамическим объектом со свободным правым концом. Поэтому алгоритм преобразования нелинейной двухточечной краевой задачи в задачу Коши с помощью инвариантного погружения, разработанный в [59], можно распространить и на другие задачи оптимального управления нелинейными динамическими объектами со свободным правым концом.
Рассмотрим задачу оптимального управления нелинейным динамическим объектом (П.2) с ограничениями на управляемые переменные
|
|
(П.3) |
и управляющие воздействия
|
|
(П.4) |
которая заключается в минимизации целевой функции
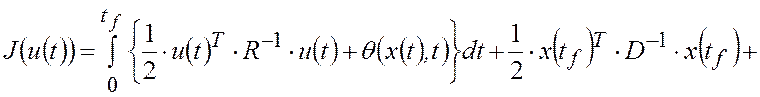
|
|
(П.5) |
Внесем второе слагаемое целевой функции (П.5) под знак интеграла, используя уравнение (П.2):
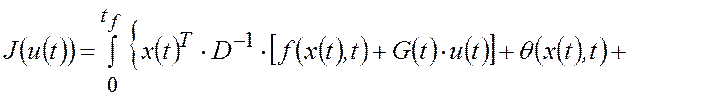
|
|
(П.6) |
С помощью принципа максимума эта задача преобразуется в следующую двухточечную краевую задачу:
|
|
(П.7) |
|
|
(П.8) |
|
|
(П.9) |
с условиями на концах траектории
|
|
(П.10) |
|
|
(П.11) |
где
|
|
(П.12) |
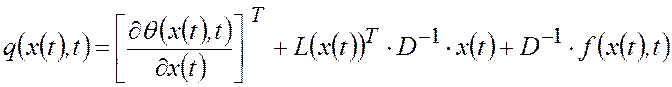 ;
;
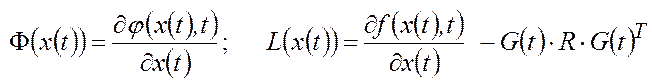 .
.
Осуществим инвариантное погружение двухточечной краевой задачи (П.8)–(П.12),
рассматривая ее как частный случай более общей задачи, когда в конце траектории
переменная ![]() имеет значение, отличное от нуля.
Рассмотрим соседние траектории, одна из которых удовлетворяет следующим
условиям в конце траектории:
имеет значение, отличное от нуля.
Рассмотрим соседние траектории, одна из которых удовлетворяет следующим
условиям в конце траектории:
|
|
(П.13) |
|
|
(П.14) |
где
неизвестное финальное значение ![]() переменной состояния
переменной состояния ![]() представляет собой линейную комбинацию
неизвестного финального значения
представляет собой линейную комбинацию
неизвестного финального значения ![]() этой переменной
состояния в случае, когда
этой переменной
состояния в случае, когда ![]() , и финального значения
переменной
, и финального значения
переменной![]() при
при ![]() .
Матрица
.
Матрица ![]() неизвестна, а момент времени
неизвестна, а момент времени ![]() и величина
и величина ![]() переменны.
Предполагается, что имеется другая траектория, для которой в конечный момент
времени
переменны.
Предполагается, что имеется другая траектория, для которой в конечный момент
времени ![]() выполняются условия
выполняются условия
|
|
|
|
(П.15) |
где
![]() и
и ![]() имеют порядок
имеют порядок ![]() по переменной
по переменной ![]() . Но, с
другой стороны,
. Но, с
другой стороны,
|
|
(П.16) |
Приравнивая правые части выражений (П.15) и (П.16), получим
|
|
(П.17) |
Если
разложить правую часть уравнения (П.17) в ряд Тейлора относительно ![]() , то это уравнение примет следующий вид:
, то это уравнение примет следующий вид:
|
|
(П.18) |
Из уравнений (П.8), (П.9) и (П.14) следует, что
|
|
(П.19) |
|
|
(П.20) |
В линейном приближении по ![]() (при
(при ![]() и
и ![]() )
уравнение (П.18) после подстановки выражений (П.19) и (П.20) примет вид
)
уравнение (П.18) после подстановки выражений (П.19) и (П.20) примет вид
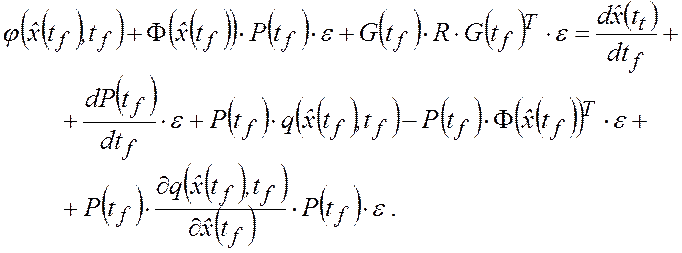
Это уравнение должно выполняться при переменном
финальном значении времени ![]() для всех достаточно
малых значений
для всех достаточно
малых значений ![]() поэтому можно выполнить его
декомпозицию на два уравнения:
поэтому можно выполнить его
декомпозицию на два уравнения:
|
|
(П.21) |
|
|
(П.22) |
Начальные условия для уравнений (П.21), (П.22) получены из условия (П.10), из которого следует, что
![]() .
.
Сравнение этого уравнения при ![]() с
выражением (П.14) приводит к следующим начальным условиям для уравнений (П.21),
(П.22):
с
выражением (П.14) приводит к следующим начальным условиям для уравнений (П.21),
(П.22):
|
|
(П.23) |
|
|
(П.24) |
Из уравнений (П.2) и (П.21) с учетом (П.12) следует, что
|
|
(П.25) |
Таким образом, нелинейная двухточечная краевая задача (П.3)–(П.6) для задачи минимизации целевой функции (П.1) при ограничении (П.2) действительно преобразована в задачу Коши для нелинейных дифференциальных уравнений (П.16), (П.17) с начальными условиями (П.18), (П.19).
Следует отметить, что инвариантное погружение двухточечных краевых задач, возникающих в результате применения принципа максимума к задачам оптимального управления с заданным условием для переменных состояния в конечный момент времени, может привести к неустойчивому алгоритму формирования управляющего воздействия. Покажем это на следующем примере.
Пример. Объект управления имеет следующее уравнение состояния:
|
|
(П.26) |
Требуется за минимальное время 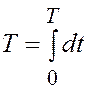 перевести
объект управления из начального состояния
перевести
объект управления из начального состояния
![]()
в конечное состояние
![]()
с помощью управляющего воздействия ![]() , непрерывно изменяющегося во времени:
, непрерывно изменяющегося во времени:
|
|
(П.27) |
при выполнении условий
![]() ,
,
![]() ,
,
где ![]() - допустимая погрешность управления (случайная величина с нулевым
средним значением и дисперсией
- допустимая погрешность управления (случайная величина с нулевым
средним значением и дисперсией ![]() );
); ![]() - требуемая траектория
изменения переменной состояния;
- требуемая траектория
изменения переменной состояния; ![]() - допустимое от-клонение переменной состояния
- допустимое от-клонение переменной состояния ![]() от
требуемой траектории
от
требуемой траектории ![]() (случайный процесс с нулевым средним
значением и дисперсией
(случайный процесс с нулевым средним
значением и дисперсией ![]() );
); ![]() - требуемое управляющее воздействие (известное);
- требуемое управляющее воздействие (известное); ![]() - допустимое отклонение управляющего воздействия
- допустимое отклонение управляющего воздействия ![]() от
требуе-мого воздействия
от
требуе-мого воздействия ![]() (случайный процесс с
нулевым средним значением и дисперсией
(случайный процесс с
нулевым средним значением и дисперсией ![]() ).
).
С помощью метода штрафных функций составим обобщенный показатель эффективности управления
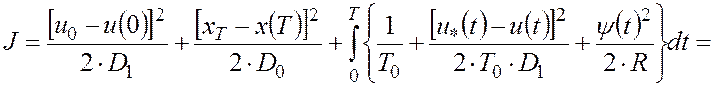
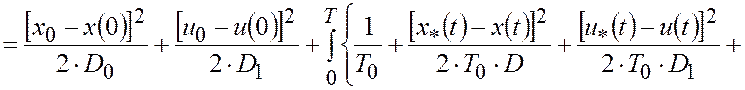
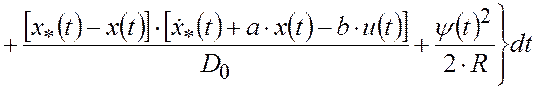 ,
,
где
![]() - требуемая
траектория изменения переменной состояния.
- требуемая
траектория изменения переменной состояния.
Уравнения Эйлера-Лагранжа этой задачи управления имеют вид
|
|
(П.28) |
|
|
(П.29) |
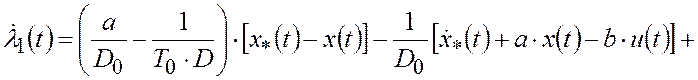
|
|
(П.30) |
|
|
(П.31) |
|
|
(П.32) |
Инвариантное погружение двухточечной краевой задачи (П.28)-(П.32) приводит к следующей задаче Коши:
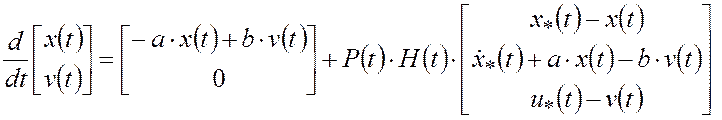 ,
,
|
|
(П.33) |
![]() ,
, ![]() ,
,
|
|
(П.34) |
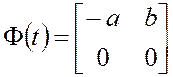 ,
, 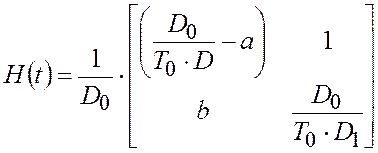 ,
,
|
|
(П.35) |
Из выражения (П.35) видно, что матрица Гессе ![]() отрицательно определена при любых
отрицательно определена при любых ![]() и
и ![]() , если
, если ![]() . Следовательно, в этом случае при
увеличении времени элементы матрицы
. Следовательно, в этом случае при
увеличении времени элементы матрицы ![]() неограниченно
возрастают, поэтому численное решение уравнения (П.33) с начальным условием (П.34)
неустойчиво.
неограниченно
возрастают, поэтому численное решение уравнения (П.33) с начальным условием (П.34)
неустойчиво.
Таким образом, инвариантное погружение является эффектив-ным методом решения двухточечных краевых задач, возникающих в задачах оптимального управления со свободным правым концом. Однако в задачах оптимального управления с фиксированным правым концом инвариантное погружение двухточечных краевых задач может привести к задаче Коши с неустойчивым решением [73]. Чтобы это не происходило, нужно вводить дополнительные ограничения в исходную постановку задачи управления, которые обеспечивают положительную определенность матрице Гессе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.