Моделирование процесса изменения уровня в двух последовательно соединённых емкостях (Лабораторная работа № 2)

Лабораторная работа № 2.

Тема лабораторной работы. Моделирование процесса изменения уровня в двух последовательно соединённых емкостях.

Цель работы. Получение практических навыков моделирования процессов изменения параметров объектов управления.

Задание. Схема двух последовательно соединённых емкостей изображена на рисунке 1.

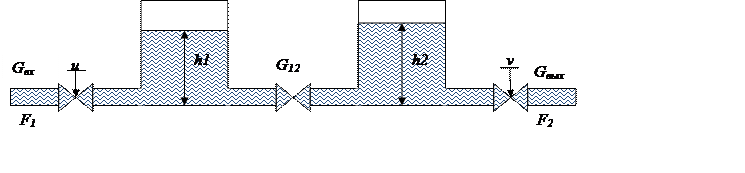
Рис. 1. Схема двух последовательно соединённых емкостей,

где:     G_вх, G_вых, G₁₂ – сопротивление трубопровода;

            F_j – площадь поперечного сечения j-ого водопровода;

            h_j – уровень жидкости в емкости j;

            u, v – управляющие воздействия на клапаны.

Уравнение закона сохранения вещества за время Δt

 ,                                                      (1)

,                                                    (2)

где: .

Заменим 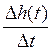 на получим:

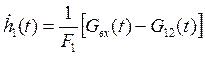,                                                    (3.1)

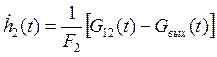,                                                  (3.2)

где:

            ,                                                                                     (4)

            ,                                                                                         (5)

            ,                                                                                  (6)

α₁, α₁₂, α₂ – параметры,

H₁, H₂ – напор жидкости на выходе и входе.

После подстановки формул (4)-(6) в (3) получим нелинейные уравнения состояния (динамики) анализируемой системы:

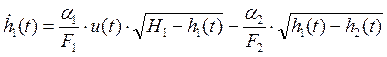                             (7.1)

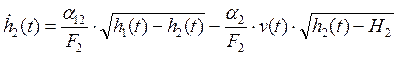                           (7.2)

В начальный момент времени t=0 система находится в устойчивом режиме. Положение клапанов в этом режиме ; , а . Поэтому начальные уровни в емкости определяют по формулам:

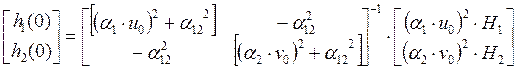               (8)

Уровнемер установлен в емкости №2 выходной сигнал уровнемера:

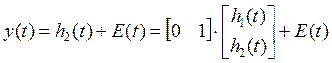,                                       (9)

где  - уровень в емкости j, значение которого определяют моделированием на ЭВМ процесса измерения уровня при заданных (измеренных) законах изменения положения штоков клапанов:, .

Линеаризованная модель системы в окрестности равновесного режима:

                                                            (10)

Модель получают разложением правых и левых частей уравнения (7) в ряд Тейлора по h₁ и h₂ в окрестности установившегося режима с обновлением линейных слагаемых.

Уравнение в отклонения от установившегося режима:

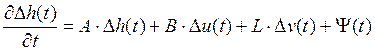,                              (11)

с начальными условиями ; ; ,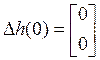

где: ; ; ; ;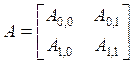

;

;

;

;

;

.

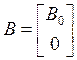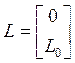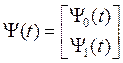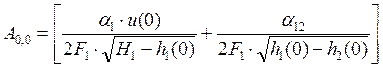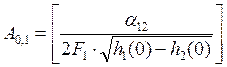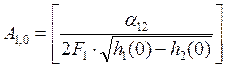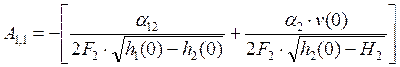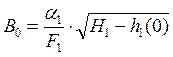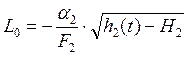Параметры системы для различных вариантов задания приведены в таблице 1.

Таблица 1 параметры системы

№ варианта	1	2	3	4	5	6	7	8	9	10	11	12	13	14
F1	1	2	3	1	2	3	4	1	2	3	4	1	2	3
F2	1	1	1	2	2	2	1	1	1	2	2	2	1	1
H1	3	4	5	6	7	2	3	4	5	4	3	5	4	4
H2	0	1	1	1	1	1	0	0	0	0	0	0	0	0
α1	2	2	1	2	1	2	1	2	2	2	1	1	1	2
α2	2	2	2	1	2	1	2	2	1	1	1	2	2	1
α12	1	1	1	1	1	1	1	1	1	1	1	1	1	1
u(0)	0,5	0,3	0,2	0,3	0,5	0,5	0,2	0,5	0,3	0,6	0,5	0,5	0,2	0,3
v(0)	0,5	0,5	0,2	0,3	0,6	0,5	0,2	0,2	0,3	0,1	0,5	0,6	0,5	0,5

№ варианта	15	16	17	18	19	20
F1	1	2	1	2	1	3
F2	2	1	2	1	1	1
H1	3	4	5	4	5	3
H2	1	1	1	1	0	1
α1	2	1	2	1	2	1
α2	2	1	2	1	2	1
α12	1	1	1	1	1	1
u(0)	0,5	0,3	0,2	0,6	0,5	0,4
v(0)	0,4	0,5	0,2	0,3	0,3	0,4

При выполнении практического занятия необходимо:

1.  Определить математическую модель системы управления в пространстве состояний;

2.  Составить дискретную нелинейную модель объекта управления (по уравнению (7). Шаг квантования времени принять равным =0,01 с.

3.  Моделированием на ЭВМ построить графики уровней емкостей  и , где (=0, 1, …, N) для нелинейной модели.

4.  Составить дискретную линеаризованную модель объекта управления (по уравнениям (10, 11). Шаг квантования времени принять равным =0,01 с.

5.  Моделированием на ЭВМ построить графики уровней емкостей  и , где (=0, 1, …, N) для линеаризованной модели.

6.  Оценить погрешность линеаризованной модели системы.

7.  Составить отчет по результатам выполнения задания.