Расчет статически определимых систем с использованием поэтажных схем

Расчет с использованием поэтажных схем

Многие балочные и рамные статически определимые системы содержат промежуточные шарниры. Для определения опорных реакций в такой системе можно составить три уравнения статики, а также уравнения моментов относительно шарниров. В итоге количество совместно решаемых уравнений будет равно числу искомых реакций плюс число промежуточных шарниров.

Однако указанный способ расчета является слишком громоздким. Поэтому сложные системы стремятся расчленить на простые элементы и рассмотреть их отдельно.

Основные и дополнительные диски. В структуре многих статически определимых систем, содержащих шарниры, можно выделить основные и дополнительные элементы (диски, балки, рамы).

Основные диски прикреплены к земле неподвижно (например, при помощи заделки или двух шарнирных опор). Удаление из сооружения основного диска приводит к изменяемости системы. В общем случае основными элементами могут быть не только отдельные стержни, но и геометрически неизменяемые и неподвижные системы.

Дополнительные (присоединенные) диски прикреплены шарнирами к основным дискам, а также могут опираться на землю. Разновидностью дополнительных являются подвесные диски, прикрепленные к двум основным или дополнительным дискам двумя шарнирами. Дополнительные диски самостоятельно использоваться не могут, так как без основных дисков они геометрически изменяемы.

Поэтажные схемы. Для наглядности расчетная схема конст­рукции, содержащей основные, дополнительные и подвесные элементы, изображается в виде поэтажной схемы (схемы взаимодействия). Естественно, предварительно надо убедиться в геометрической неизменяемости системы, для чего проводится кинематический анализ.

При составлении поэтажной схемы используются следующие  принципы:

§ основные диски считаются I этажом;

§ дополнительные и подвесные диски могут быть II, III, ... этажами;

§ каждый из шарниров, соединяющих основные и дополнительные диски, заменяется шарнирно неподвижной опорой;

§ один из шарниров, присоединяющих подвесной диск, заменяется шарнирно неподвижной опорой, другой – шарнирно подвижной; при этом в опору нижележащего диска добавляется один стержень;

§ полученная поэтажная схема и каждый ее элемент в отдельности  должны быть геометрически неизменяемыми.

На рисунке 3.3 изображена двухпролетная статически определимая рама и ее поэтажная схема. Средняя часть рамы геометрически неизменяема и неподвижна, поэтому она является основным диском. 

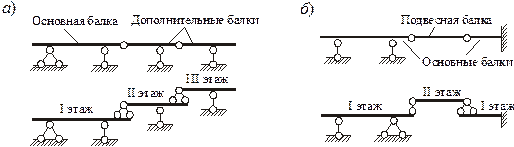
Рисунок

Далее можно исследовать каждый элемент поэтажной схемы отдельно. Расчет начинается с верхних этажей, на которые действует только заданная нагрузка. Затем рассчитываются нижние этажи, на которые, кроме приложенной нагрузки, действуют силы в виде опорных давлений верхних этажей. Эпюры внутренних усилий обычно строятся на одной базе для всей системы.

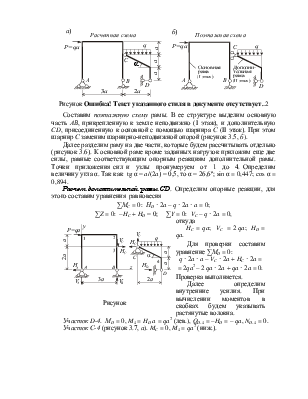
Пример 1 Требуется рассчитать статически определимую раму, которая состоит из двух элементов АВ и СD, соединенных шарниром. Расчетная схема рамы показана на рисунке 3.5, а.

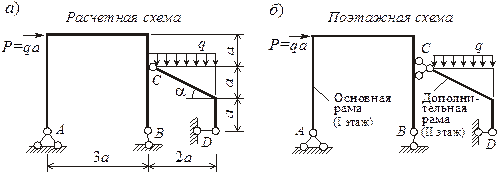
Рисунок 3.5

Составим поэтажную схему рамы. В ее структуре выделим основную часть АВ, прикрепленную к земле неподвижно (I этаж), и дополнительную CD, присоединенную к основной с помощью шарнира С (II этаж). При этом шарнир С заменим шарнирно-неподвижной опорой (рисунок 3.5, б).

Далее разделим раму на две части, которые будем рассчитывать отдельно (рисунок 3.6). К основной раме кроме заданных нагрузок приложим еще две силы, равные соответствующим опорным реакциям дополнительной рамы.  Точки  приложения сил и  узлы  пронумеруем  от  1  до  4. Определим  величину угла α. Так как  tg α = a/(2a) = 0,5, то α = 26,6º; sin α = 0,447; cos α = 0,894.

Расчет дополнительной рамы CD. Определим опорные реакции, для этого составим уравнения  равновесия 

∑М_C = 0:  Н_D · 2a – q · 2a · a = 0;

∑Z = 0:  –H_C + H_D = 0;     ∑Y = 0:  V_C – q · 2a = 0,

Участок D-4.  М_D = 0, M₄ = H_Da = qa² (лев.), Q_D-4 = –H_D = – qa, N_D-4 = 0.

Участок С-4 (рисунок 3.7, а). M_C = 0, M₄ = qa² (ниж.).

Максимальный момент

M_max = V_C z'₀ cos α – H_C · z'₀ sin α – q· 0,5 · (z'₀ cos α)² = 2 qa· 1,68 a · 0,894 –

– qa· 1,68 a · 0,447  – q· 0,5 · (1,68 a · 0,894)² = 1,125 qa².

Расчет основной рамы АВ. Определим опорные реакции, для этого составим уравнения  равновесия 

∑М_В = 0:  V_B · 3a – P · 3a – H_C · 2a – V_C · 3a = 0;

∑М_A = 0:  V_A · 3a – P · 3a – H_C · 2a = 0;    ∑Z = 0:  –H_A + H_C + P = 0,

откуда

V_A = 1,667 qa;  V_B  = 3,667 qa;  H_A = 2 qa.

Для проверки составим уравнение  ∑Y = 0:

V_B – V_A – V_C = 3,667 qa –1,667 qa – 2 qa = 0.

Проверка выполняется.

Далее определим внутренние усилия.

Участок A-1.  М_A = 0, M₁ = H_A · 3a = 2qa · 3a = 6qa² (прав.),

Q_A-1 = H_A = 2 qa,  N_A-1 = V_A = (5/3) qa.

Участок 1-2. M₁ = 6qa² (ниж.), M₂ = H_C · a = qa · a = qa² (ниж.),

Q_1-2 = –V_A = –1,667 qa,  N_1-2 = H_A = 2 qa.

Участок 2-3.  М₂ = qa² (лев.), M₃ = 0,

Q_2-3 = –H_С = – qa,  N_2-3 = –V_A = –1,667 qa.

Участок В-3.  М_В = M₃ = 0, Q_В-3 = 0, N_В-3 = –V_В = –3,667 qa.

По полученным данным строим эпюры (см. рисунок 3.8). ý

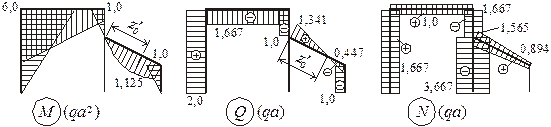
Рисунок 3.8

Таким образом, поэтажная схема делает более понятной работу сложной системы и упрощает ее расчет. Пример расчета многопролетной балки с использованием поэтажной схемы будет рассмотрен далее.