Расчет многопролетной балки на неподвижную нагрузку

Пример 1

Расчет многопролетной балки на неподвижную нагрузку

Для статически определимой многопролетной балки требуется:

1.  Вычертить в масштабе расчетную схему.

2.  Выполнить кинематический и структурный анализ балки.

3.  Используя поэтажную схему балки, построить эпюры поперечных сил Q и изгибающих моментов M от заданной нагрузки.

4.  Определить опорную реакцию (любую) основной балки кинематическим методом.

Расчет

1. Расчетная схема.

рисунок

2. Анализ геометрической неизменяемости.

рисунок

2.1 Кинематический анализ балки

Балка статически определима и может быть геометрически неизменяема.

2.2Структурный анализ

рисунок

D₁ + D₂ – геометрически неизменяемая часть, т.к. эти два диска соединены при помощи заделки, то есть по правилу объединения двух дисков.

 (D₁ + D₄)+ D₂ + D₃ – геометрически неизменяемое тело, т.к. эти три диска соединены при помощи двух шарниров (1,2) и пары кинематических связей B,C , т.е. по правилу комплексного соединения трех дисков.

Следовательно многопролетная балка геометрически неизменяемая.

3. Построение эпюр Q, M методом сечений с использованием поэтажной схемы.

рисунок

3.1 Расчет дополнительной балки (2-С).

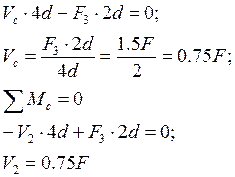
Определение ординат.

Эпюра Q.

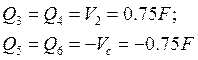
Эпюра M.

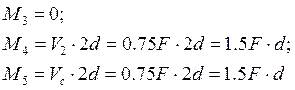
3.2 Расчет дополнительной балки (1 - 2).

∑M₁=0;

- V₂ · 5d + V_B · 4d – F₂ · 2d = 0;

 V_B=;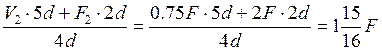

∑M_B=0;

- V₁ · 4d + F₂ · 2d – V₂ · d =0;

V₁=.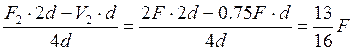

Проверка:

V₁ – V₂ – F₂ + V_В =0;

;

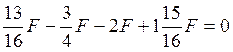0=0.

Эпюра Q.

Q₁₂ =;

Q₁₁ =;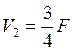

Q₁₀ =;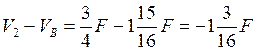

Q₉ =Q₁₀ =;

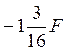Q₈ =V₂ – V_B + F₂ =;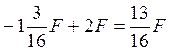

Q₇ =Q₈ =.

Эпюра M.

M₁₂ =0;

M₁₁ =;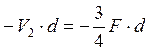

M₁₀ =;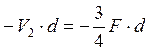

M₉ =;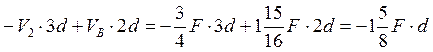

M₈ =M₉ =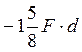;          M₇=   =;

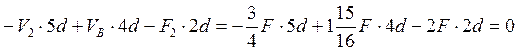3.3 Расчет основной балки А1 .

∑y=0;

V_A – F₁' =0;

V_A =F₁' =V₁ =;

Эпюра Q

Q₁₃ =Q₁₄ =V₁ =;

Эпюра M

∑M_A=0;

- V₁ · 2d – M_A =0;

M_A = -V₁ · 2d =;

∑M₁=0;

V_A · 2d – M_A = 0;

0=0.

4. Определяем опорную реакцию основной балки кинематическим методом. 

рисунок

 _; ;

 _; ;

 _; ;

;

.

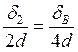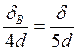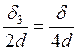Пример 2

Для металлической фермы с размерами и узловыми нагрузками, показанной на схеме требуется:

1.  Вычертить в масштабе расчетную схему.

2.  Выполнить кинематический и структурный анализ фермы.

3.  Вычислить усилия во всех стержнях фермы способом вырезания узлов.

4.  Рассчитать усилия в отмеченных стержнях методом сечений.

Расчет

1. Расчетная схема.

рисунок

2. Выполняем анализ геометрической неизменяемости фермы.

2.1 кинематический анализ

W =2Y – D – C_o;

Y=8; D=13; C_o=3;

W=2 · 8 – 13 – 3 =0;

Значит, ферма статически определима и может быть геометрически неизменяемой.

2.2 структурный анализ

рисунок

D₁+D₂+D₃ – геометрически неизменяемая часть, т.к. объединены три диска при помощи трех шарниров не лежащих на одной прямой , т.е. по правилу объединения трех дисков Ф₁.

Ф₁ + шарнир5(D₄,D₇) – по правилу диад: геометрически неизменяемая часть – Ф₂ .

Ф₂ + шарнир2(D₆,D₅) – по правилу диад: геометрически неизменяемая часть – Ф₃ .

Ф₃ + шарнир3(D₉,D₁₁) – по правилу диад: геометрически неизменяемая часть – Ф₄.

Ф₄ + шарнир4(D₁₀,D₈) – по правилу диад: геометрически неизменяемая часть – Ф₅ .

Ф₅ + шарнирB(D₁₃,D₁₂) – по правилу диад: геометрически неизменяемая часть – Ф₆ .

Ф₆ – «земля» (по правилу объединения двух дисков).

Значит, вся расчетная схема геометрически неизменяема.

3. Рассчитываем ферму на заданную нагрузку способом вырезания узлов.

3.1 Определяем опорные реакции.

∑M_A=0;

;

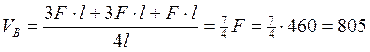кН;

∑M_B=0;

;

кН;

Проверка

∑y=0;

;

575 – 460 – 460 – 460 + 805=0;

0=0;

3.2 Определяем усилия во всех стержнях способом вырезания узлов.

Сводим расчеты в таблицу

4.Расчет усилий в отмеченных стержнях методом сечений

рисунок

4.1 Сечение 1-1 левая часть (способ сечений)

4.2 Сечение 2-2 левая часть (способ моментной точки)

23 – исследуемое сечение 2 оставшиеся стержни пересекаются в моментной точке 5

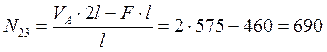кН

4.3 Сечение 3-3 правая часть (способ сечений)

4-3 – исследуемый стержень

кН.