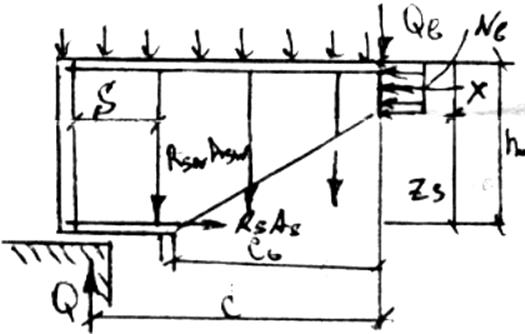
Строительство и архитектура \ Строительные конструкции

Ответы на экзаменационные вопросы № 1-25 дисциплины "Строительные конструкции" (Бетон. Классы и марки бетона. Стальные формы для изготовления СЖБИ. Назначение и виды форм), страница 5


9. Расчет прочности изгибаемых эл-тов по наклонным сечениям на действие поперечной силы опред. Шага хомутов.

Разрушение изгибаемого элемента по наклонному сечению происходит в следствии одновременного действия на него поперечных сил и изгибаемых моментов.

Прочность элементов по наклонному сечению на действие поперечной силы обеспечивается условие: QQb+Qsw +Qsinc, где Q-поперечная сила, от действия опорной реакции и нагрузки; Qb-поперечная сила, воспринимаемая в сжатой зоне над наклонными сечениями; Qsw-сумма осевых усилий в поперечных стержнях (хомутах) пересекаемых наклонным сечением; Qsin c-сумма проекций на нормаль к оси элемента осевых усилий в отгибах, пересекаемых наклонным сечением.

Расстояние между хомутами S: ,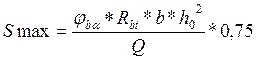

0,75-коэф. учитывающий неточность установки хомутов

Расчет поперечных стержней формулы

,

,

,

,

.

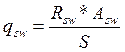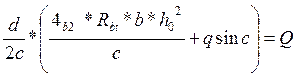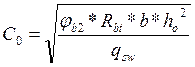Для исключения образовавшихся трещин м/д 2мл соседними хомутами ограничить шаг, в этом случае поперечная сила должна восприниматься только бетонном:

.

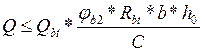Для пролетного участка при h>300мм

.

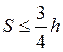10. Расчёт прочности внецентренно сжатых элементов.

 Случай симметричного армирования.

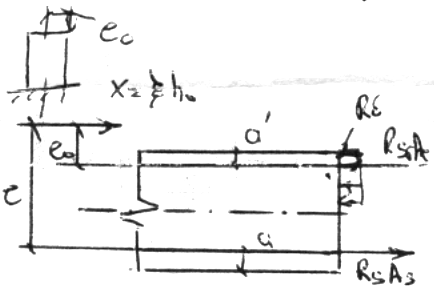Внецентренно сжатые элементы испытывают воздействие продольно сжимающей силы смещённой относительно центра тяжести.

, при l0/h≥4, η – не учитывается, l0 – расчётная длина сечения

;

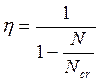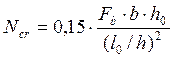
      Подбор не симметричной арматуры:

1)  ξ = ξR;   

2)   =>           ;   ;

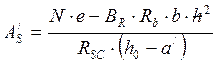3) 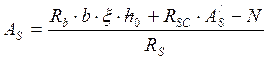; если AS≤0, то ,  μmin = 0,05-0,25%

     ; ;

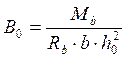
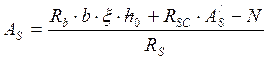; ; ; MИ≥N·e.

Подбор симметричной арматуры:

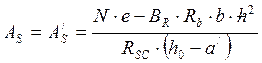; RS=RSC;.

1) 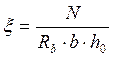 ; ξ≤ξR;

2)   ;

3)   AS=A/S.

 

11. Расчёт прочности центрально и внецентренно растянутых элементов.

Расчёт прочности центрально растянутых элементов

Разрушение центрально – растянутых элементов происходит после того, как в бетоне образуются сквозные трещины и он в этих местах выключается из работы, а в арматуре напряжения достигают предела текучести (если сталь имеет площадку текучести) или временного сопротивления. Несущая способность центрально – растянутого элемента обусловлена предельным сопротивлением арматуры без участия бетона.

Трещины не образуются, если N≤Ncre, где N – внешняя нагрузка, Ncre – усилие, которое может воспринять сечение при образовании трещин. Для элементов без предварительного напряжения .

 Для преднапряжённых элементов ,

где P – усилие предварительного обжатия, которое на стадии эксплуатации определяется с учётом всех первых потерь.

Расчёт прочности внецентренно растянутых элементов.

          Предельное состояние по несущей способности элемента любого симметричного сечения, внецентренно растянутых в плоскости симметрии, характеризуется тем, что бетон пересечён сквозными трещинами, внешнему усилию сопротивляется лишь продольная арматура. Разрушение элемента наступает, когда напряжение в продольной арматуре достигают предельного значения. Расчёт производится из условия Mr≤Mcre,

где  Mr – момент внешних сил, расположенных по одну сторону от рассматриваемого сечения относительно оси параллельной нулевой линии и проходящей через точку ядра сечения наиболее удалённую от растянутой зоны. ,

где e0 – эксцентриситет внешних сил относительно центра тяжести приведенного сечения, r – расстояние от центра тяжести до самой удалённой точки ядра сечения в растянутой зоне, Mcre – сумма моментов всех внешних сил при образовании трещины.

, ,

где Wpl – пластический момент сопротивления, ;  y=1,75 для прямоугольного сечения и таврового с полкой в сжатой зоне. , Mrp – момент обжатия силы Р в точке наиболее удалённой от растянутой зоны.

12. Преднапряженные ж/б элементы. Способы создания предварительного напряжения. Анкеровка напрягаемой арматуры

Преднапряженные элементы это изделия с использованием предварительно напряженной арматуры. Применение преднапряжения позволяет: уменьшить расход стали, бетона и вес конструкции, увеличить трещинностойкость, жесткость, срок службы конструкции и выносливость при многократных кратковременных нагружениях, уменьшить прогиб.

Различают две схемы создания преднапряжения:

1.  Натяжение арматуры на упоры формы.

2.  Натяжение арматуры на затвердевший бетон.

Скачать файл