Составление уравнений систем автоматического управления (Практическое занятие № 1)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Электронные вычислительные машины»

Основы теории управления

Методические указания для практических занятий

для студентов дневного и вечернего обучения  по специальности 220100

«Вычислительные машины, комплексы, системы и сети»

Тула 2001

Разработали:    д.т.н.,  проф. Карпов В.С.

                          к.т.н., доц. Ю.И. Лебеденко

Данные методические указания предназначены для студентов специальностей 220100 «Вычислительные машины, комплексы, системы и сети»,  181300 «Электрооборудование и электрохозяйство предприятий, организаций и учреждений», изучающих основы теории управления в качестве общетехнической дисциплины в третьем учебном семестре. Предполагается, что студенты обладают необходимыми знаниями по высшей математике, физике, электротехнике и основам электроники.

СОДЕРЖАНИЕ

Практическое занятие 1

Составление уравнений систем автоматического управления……………………….4

Практическое занятие 2

Решение дифференциальных уравнений системы управления с помощью преобразования Лапласа ……………………………………………………………………………8

Практическое занятие 3

Элементарные звенья динамических систем. Временные характеристики звеньев ………………………………………………………………………………………..11

Практическое занятие 4

Преобразование структурных схем систем управления………………………..16

Практическое занятие  5

Частотные характеристики линейных динамических систем …………………22

Практическое занятие 6

Анализ устойчивости линейных динамических систем …………………………27

Практическое занятие 7

Анализ точности автоматических систем …………………………………… ….31

Практическое занятие 8

Коррекция систем автоматического регулирования ……………………………..36

Библиографический список ………………………………………………………………………………………. 40

Практическое занятие 1

Составление уравнений систем автоматического управления

1.1.  Теоретические положения

При составлении дифференциальных уравнений систем автоматического управления всегда используются физические законы, описывающие конкретное техническое устройство, механизм, прибор. Порядок составления дифференциальных уравнений системы лучше всего рассмотреть на примере.

Рассмотрим следящий электромеханический привод (рис.1.1):

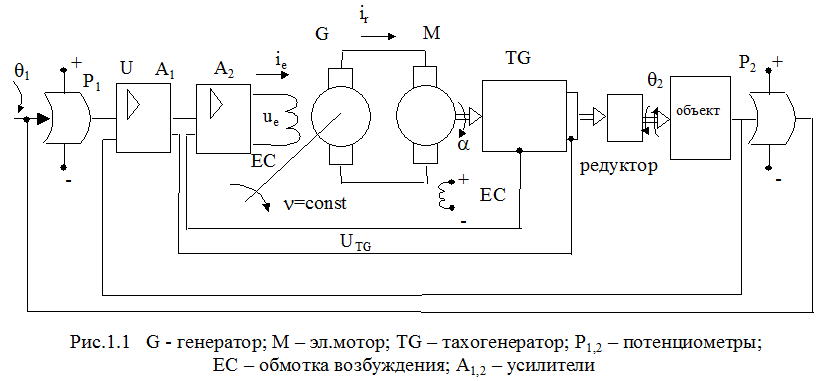
В этой системе q₁ - входной угол; q₂ - выходной угол поворота объекта управления. Их разность (q₁ -q₂)служит сигналом управления для двигателя.

Для каждого отдельного узла сервопривода можно написать дифференциальное или алгебраическое уравнение:

1)  Чувствительный элемент:

Выходное напряжение потенциометра  P₁ определиться как

 U₁=k₁q₁.

На выходе  P₂ имеем:

 U₂=k₁q₂,

где k₁-коэффициент передачи потенциометра. Следовательно

U=U₁-U₂=k₁(q₁-q₂)=k₁q.

2)  Усилители. Если рассматривать их как безынерционные элементы с помощью коэффициентами передачи k₂ и k₃, то с учетом того, что на входе второго усилителя выход первого суммируется с сигналом обратной связи тахогенератора, получим:

U_e=(k₂U-U_tg)k₃

3)  Обмотка возбуждения генератора. Дифференциальное уравнение можно записать на основе закона Кирхгофа:

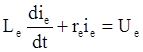
где L_e и r_e –величины индуктивности и активного сопротивления обмотки.

4)  Генератор. Для генератора с линейной характеристикой  ЭДС может быть вычислена по формуле:

e=k₅i_e;        ;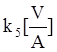

5)  Электродвигатель имеет две степени свободы. Соответственно, его описание будет иметь два дифференциальных уравнения первого порядка:

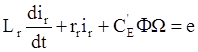 - для электрической части

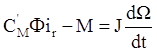 - для механической части.

где L_r и  r_r – индуктивность и активное сопротивление обмотки ротора,

 С’_E и С’_М - коэффициенты пропорциональности,

J – момент инерции, приведенный к оси двигателя,

 W - угловая скорость ротора,

 M – момент нагрузки.

Если считать магнитный поток возбуждения двигателя постоянным, F=const, то

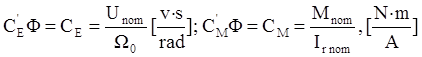
где U_nom, M_nom, I_{r nom} – номинальные значения напряжения ан двигателе, вращающего момента и тока якоря;

W₀ – угловая скорость ротора без нагрузки.

Угол вращения двигателя связан со скоростью через простое соотношение

 .

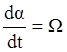6)  Редуктор. Если характеристика механизма линейная, то ее можно описать алгебраическим выражением:

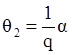
где q – коэффициент передачи редуктора.

7)  Тахогенератор. Выходное напряжение этого устройства пропорционально скорости вращения двигателя:

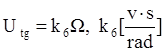
Объединим все уравнения компонентов  в единую систему

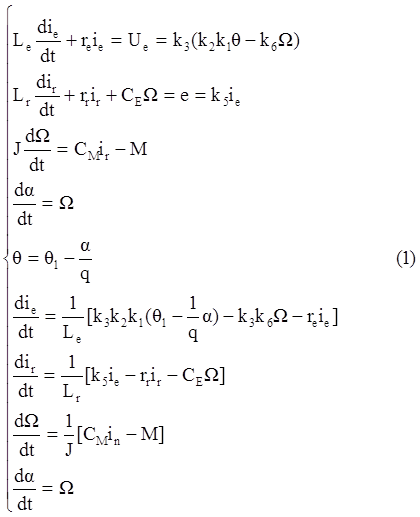
В этой системе в качестве входного воздействия выступает θ₁[rad], как возмущающее воздействие . В ней можно выделить четыре независимых переменных: θ₂[rad] – выход; Ω [rad/s]; i_r[A] и i_e[A].

Выведенные уравнения можно привести к относительным единицам. Для этого примем в качестве основной одну из фазовых переменных (чаще всего это выходная величина), измеряемую в конкретных физических единицах.

После этого можно пересчитать все коэффициенты в уравнениях так, чтобы они выражались в безразмерных единицах:

Пусть i_e = x₁; i_r = x₂;  Ω = x₃; α = x₄;  θ₁ = y₁; M = y₂.

Тогда

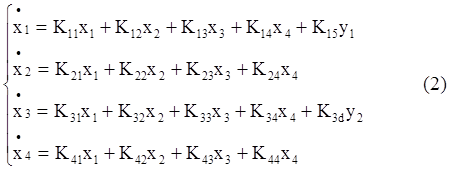
Легко видеть, что многие K_ij  равны нулю в системе (2).

будем называть фазовыми координатами.

Для данной системы можно записать одно дифференциальное уравнение четвертого порядка

,

В общем виде:

(a₄p⁴+a₃p³+a₂p²+a₁p+a₀)x=y₁b₁+y₂b₂                  (3),

или в еще более отвлеченной форме:

   D(p)x(t)=Q(p)g(t)+N(p)f(p).

Это уравнение дает сокращенную форму записи дифференциальных уравнений системы через передаточные функции.

1.2.  Практические задания

1) Операционный усилитель имеет обратную связь с RC-цепью (рис.1.2)

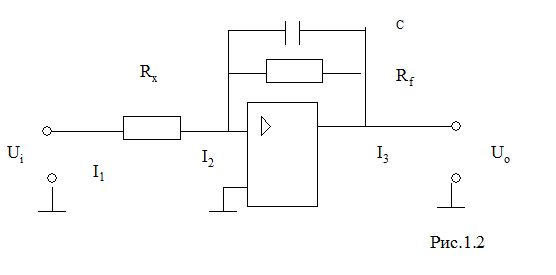
Составить систему дифференциальных уравнений

Ответ: .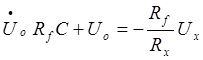

2) Выполните задание 1, если в обратной связи стоит только конденсатор C.

Ответ: .

1.3.  Контрольные вопросы

1)  Что называется динамической системой?

2)  Приведите основные признаки классификации динамических систем.

3)  Дайте определения объекта регулирования и регулятора.

4)  Поясните принципы управления по разомкнутому и замкнутому контуру.

5)  В чем различие между прямым и непрямым регулированием?

6)  Перечислите основные функциональные элементы системы автоматического регулирования.

7)  Как осуществляется переход от физических узлов системы к их математическому описанию?

8)  Почему к системам автоматического управления часто применяется процедура линеаризации?

9)  Что называется безразмерной системой уравнений?

10)  Для чего служит передаточная функция системы?