Дискретные системы автоматического регулирования. Методы исследования дискретных систем. Z-преобразование

Лекция 15

Дискретные системы автоматического регулирования

План:

1.  Понятие дискретной  динамической системы

2.  Разностные уравнения

3.  Методы исследования дискретных систем. Z –преобразование

4.  Устойчивость и качество управления в дискретных системах

Линейной импульсной системой управления называется система, которая кроме линейных звеньев, описываемых линейными дифференциальными уравнениями, содержит хотя бы одно импульсное звено, преобразующее непрерывный сигнал в последовательность импульсов, выдаваемых с определенным периодом.

Выходной сигнал идеального импульсного звена может быть представлен решетчатой функцией, т.е. функцией, состоящей из последовательности дельта - импульсов, умноженных на некоторые коэффициенты. Реальные импульсные звенья обычно вырабатывают сигнал в виде импульсов с конечной длительностью и  амплитудой. При различных типах импульсной модуляции меняют амплитуду или ширину импульсов пропорционально входному сигналу. Однако если время импульса существенно меньше, чем время паузы между импульсами, то реальное импульсное звено можно представить последовательным соединением идеального импульсного звена и непрерывной части.

В общем виде дискретную систему можно представить в виде схемы (рис.1):

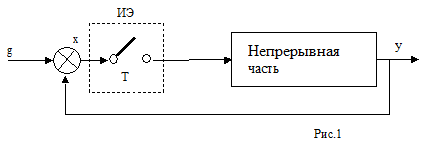
На рисунке идеальный импульсный элемент (ИЭ) представлен в виде ключа, который замыкается с периодом Т.  Время замыкания считается бесконечно малым, поэтому выходной сигнал ИЭ можно представить в виде решетчатой функции (последовательности дельта – импульсов). Этот сигнал .является входным сигналом для непрерывной части, которую для линейной системы можно описать с помощью передаточной функции. В соответствии с этим и выходной сигнал непрерывной части можно представить решетчатой функцией: y[nT]   или y[n].  Если рассматривать относительное временное смещение  внутри периода дискретизации Т, можно использовать смещенную решетчатую функцию y[n, ].

В теории дискретных систем вместо дифференциальных уравнений используются уравнения в конечных разностях. Для решетчатой функции f[n] разностное уравнение первого порядка будет иметь вид:

Конечная разность второго порядка определяется как

и так далее.

Уравнение в конечных разностях порядка  m имеет общую форму:

или

,

где a₀, a₁…a_m зависят от  b₀, b₁,…b_m.

Уравнение в конечных разностях может быть получено из рекуррентных формул, которые позволяют вычислить y[n+m] для n=0,1,2… при заданных величинах y[0], y[1]…y[m-1]. Эти вычисления легко произвести с помощью ЭВМ.

Общее решение уравнения в конечных разностях может быть записано в виде:

,

где C_i – константы, z_i – корни характеристического уравнения

.

Выполнение условия |z_i|<1 (i=1,2 .. .m) позволяет судить об устойчивости дискретной системы. Для исследования импульсных систем широко применятся дискретное преобразование Лапласа и  z-преобразование. Дискретное преобразование Лапласа определяется формулой

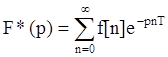
или

.

Если выполнить подстановку z=e^pT , то мы перейдем к  z – преобразованию:

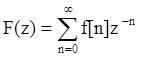
или

.

Эти формулы можно применить и для смещенной решетчатой функции:

Это изображение можно получить и для непрерывной функции времени при заданном  периоде дискретизации:

Легко доказать, что преобразование Лапласа  дискретной функции эквивалентно  z-преобразованию исходной непрерывной функции:

.

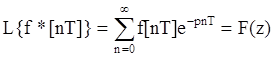Приведем основные свойства z-преобразования.

1.  Свойство линейности:

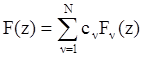 для .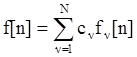

2.  Теорема запаздывания:

.

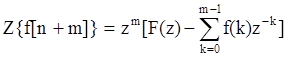3.  Умножение оригинала на экспоненту:

.

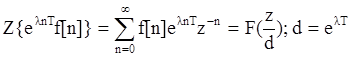4.  Изображение конечной разности:

.

5.  Изображение решетчатой функции с измененным периодом следования:

.

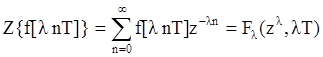6.  Сумма ординат решетчатой функции:

.

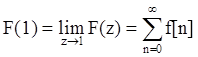7.  Конечное значение решетчатой функции:

.

8.  Начальное значение решетчатой функции:

.

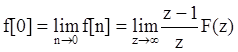9.  Свертка решетчатых функций:

.

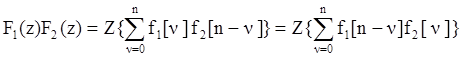10.  Обратное  Z-преобразование:

.

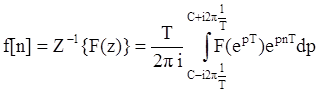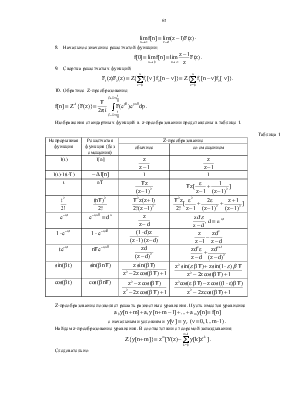
Изображения стандартных функций в  z-преобразовании представлены в таблице 1.

Таблица 1

Z-преобразование позволяет решать разностные уравнения. Пусть имеется уравнение

с начальными условиями .

Найдем z-преобразование уравнения. В соответствии с теоремой запаздывания:

.

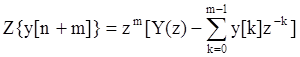Следовательно

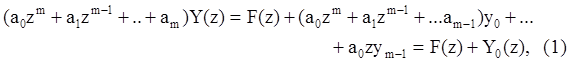
где Y₀(z) – составляющая, определяемая начальными условиями.

Из выражения (1) легко получить изображение результирующей решетчатой функции:

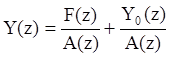, где

(аналогично преобразованию Лапласа для непрерывных функций).

Рассмотрим импульсную систему (рис.2a) в которой решетчатая функция x^*[n] является входным сигналом экстраполятора (W_E(p)), с выхода которого сигнал подается на линейную часть W₀(p).