Дискретные системы автоматического регулирования. Методы исследования дискретных систем. Z-преобразование, страница 2

Если записать входной сигнал в виде  , то можно представить выходной сигнал системы как

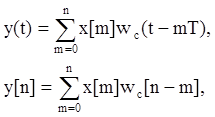
где  - весовая функция непрерывной части:

.

Используем z-преобразование:

.

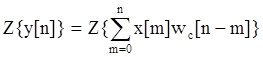В соответствии с теоремой свертки:

Y(z)=W(z)X(z),

Где 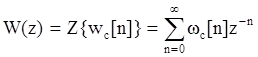  - импульсная передаточная функция непрерывной части.

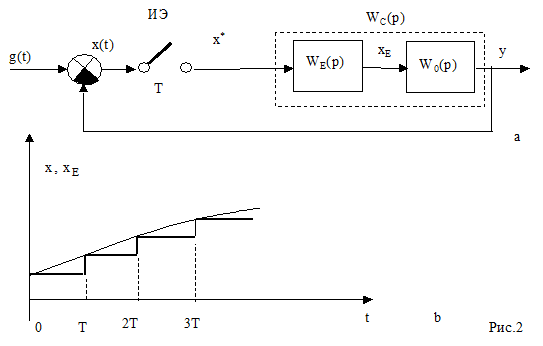
В реальных импульсных системах обычно используется экстраполятор с фиксацией входного значения на периоде  (Рис.2b). В этом случае передаточная функция экстраполятора, называемого экстраполятором нулевого порядка, будет равна

.

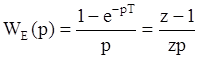Передаточная функция разомкнутой системы в общем случае (при наличии смещения по времени) будет определяться как:

,

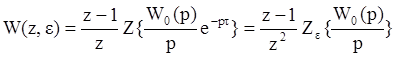где    .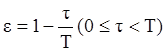

Для   .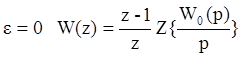

Например:

;

.

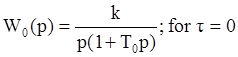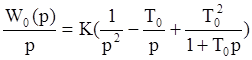В соответствии с предыдущей таблицей:

,

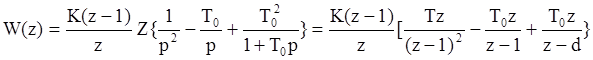где   

.

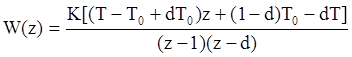Для замкнутой системы (рис.2a) импульсная передаточная функция будет иметь вид:

.

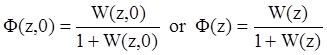Она связывает величины входного  и выходного  сигналов через z-преобразование: . Аналогично с непрерывными системами можно ввести передаточную функцию по ошибке для замкнутой системы:

.

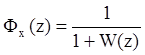Вообще говоря, все свойства линейных передаточных функций, связанные со структурными преобразованиями (последовательное и параллельное соединения, перенос узлов и сумматоров) могут быть расширены на область дискретных передаточных функций.

Для импульсных систем можно также ввести понятие частотной передаточной функции (частотной характеристики):

.

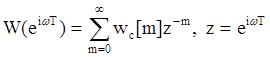С использованием этой характеристики можно найти амплитуду и фазу  выходного сигнала системы.

Устойчивость импульсной системы, как и в случае непрерывных систем, определяется распределением корней характеристического уравнения. Для устойчивости они должны имет отричательную действительную часть, а границей устойчивости является мнимая ось комплексной плоскости.  Когда используется  z-преобразование, подстановка   преобразует эту ось в окружность единичного радиуса. Следовательно, для устойчивости необходимо, чтобы характеристическое уравнение, полученное из передаточной функции разомкнутой импульсной системы

1+W(z)=0

Должно иметь все корни, лежащие внутри круга, описанного вокруг начала координат с единичным радиусом на  z-плоскости:

|z_i|<1.

Например, для системы первого порядка с характеристическим уравнением  z+A=0 условие устойчивости имеет вид |A|<1 .

Для системы второго порядка:

z²+Az+B=0                        (2)

условия устойчивости имеют вид

.

Для систем более высокого порядка исследование устойчивости с помощью характеристического уравнения более трудоемко. Иногда для решения этой задачи используют  w - преобразование (конформное преобразование):

.

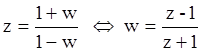Заменяя z на , получим:

,

где 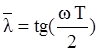 - относительная псевдочастота.

Абсолютная псевдочастота определяется формулой:

.

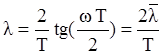Для малых значений частоты :

.

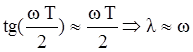Поэтому для частот, удовлетворяющих условию  можно заменить псевдочастоту реальной частотой. Это свойство можо использовать для вычисления  установившейся ошибки при гармоническом входном сигнале.

Легко видеть, что для изменения частоты в диапазоне (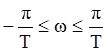) величина псевдочастоты изменяется от  до  и точка, соответствующая комплексной величине  w перемещается вдоль мнимой оси. Следовательно, мнимая ось для  w – преобразования является границей области устойчивости: облать устойчивости расположена слева от мнимой оси  для корней характеристического уравнения, записанного  для w -преобразования. Например, используя  w – преобразование, уравнение (2) может быть преобразовно к виду

.

В соответствии с критерием устойчивости для линейных систем, коэффициенты характеристического уравнения системы второго порядка должны быть положительными. Это приводит к ранее полученным условиям устойчивости (3).

Для определения  устойчивости замкнутой импульсной системы можно  использовать критерий Найквиста. Как для z –преобразования, так и для w-преобразования, амплитудно-фазовая характеристика разомкнутой системы для устойчивости замкнутой не должна охватывать точку (-1, i0).

Следует иметь в виду, что для W(z), характеристика W() является периодической функцией  с периодом .

Рассмотрим пример: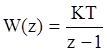

.

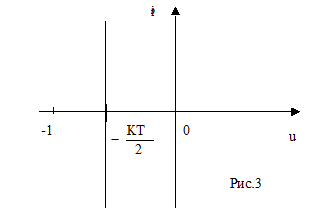
В координатах (u,) характеристика W() представляет собой вертикальную прямую линию (рис.3). Отсюда можно найти условие устойчивости KT<2.

Если выполнить для передаточной функции  W(z) w-преобразование, то получим передаточную функцию разомкнутой системы в виде:

.

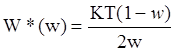Выполним подстановку :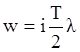

.

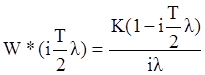Таким образом, w-преобразование дает непериодическую функцию псевдочастоты, а потому для псевдочастоты возможно построение асимптотической ЛАЧХ.

Используя указанный путь можно получит дискретную передаточную функцию и для замкнутой системы  по полезному сигналу  и по ошибке . Аналогично строятся и псевдочастотные характеристик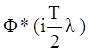и  и .

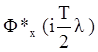В простых дискретных системах оценка качества регулирования  производится также, как и для линейных систем: построив кривые переходных процессов или используя частотные критерии качества. Наиболее простым является использование  коэффициента колебательности. Как и в линейных системах, приемлемое значение коэффициента колебательности обеспечивается, когда АФЧХ не пересекает границу запретной области, расположенной  в круге с центром в (-1, i0).