Исследование электрического состояния трехфазной цепи синусоидального тока при соединении приемников звездой (Лабораторная работа № 1.8)

Лабораторная работа N 1.8

Исследование электрического состояния трехфазной цепи синусоидального тока при соединении приемников звездой

Цель работы:

·  научиться определять нейтральный и линейные провода трехфазной четырехпроводной сети;

·  исследовать влияние изменения параметров одного из трех однофазных приемников, а также влияние обрыва нейтрального и линейного проводов на работу трехфазной цепи (на соотношение линейных и фазовых напряжений, на ток в нейтральном проводе, на суммарную активную мощность трехфазной цепи);

·  научиться строить по опытным данным векторно-топографические диаграммы напряжений, совмещенные с векторными диаграммами токов.

1. Краткие теоретические сведения

1.1. Основные понятия и величины

На рис.8.1 приведена схема трехфазной цепи при соединении обмоток генератора и фаз приемника звездой. При этом потенциал точки Nсоединения концов X, Y и Z обмоток фаз генератора принимается равным нулю. Концы x, y, z фаз приемника также соединены в одну точку n. Точки N и n называют нейтральными, а провод, их соединяющий, - нейтральным. Провода Aa, Bb и Cc, соединяющие начала фаз генератора (трансформатора) и  приемника, называют линейными.

 

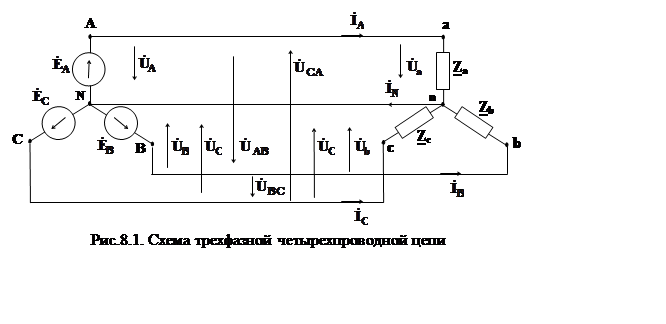Положительное направление токов в фазах генератора совпадает с положительным направлением ЭДС, а положительные направления напряжений на фазах приемников совпадают с направлениями токов в фазах приемников. Положительные направления напряжений на фазах генератора противоположны направлениям соответствующих ЭДС рис.8.1.Так как обмотка генератора, линейный провод и приемник, принадлежащий одной фазе, соединены последовательно, то, при соединении звездой, линейный ток  равен фазному току

.                                               (8.1)

Соотношения между линейными и фазными напряжениями можно получить из уравнений, записываемых по второму закону Кирхгофа для контуров ANBA, BNCB и CNAC

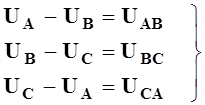                                       (8.2)

При этом, для симметричного трехфазного генератора соотношение между действующими значениями фазных и линейных напряжений имеет вид

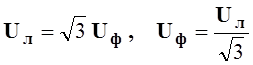.                                    (8.3)

1.2. Расчет трехфазной цепи при соединении “звезда-звезда”

Если пренебречь сопротивлениями проводов, то фазные напряжения приемника в четырехпроводной цепи рис.8.1 равны фазным напряжениям источника (генератора или трансформатора)

.                         (8.4)

При этой схеме соединения источника и приемника, токи в фазах определяются по закону Ома

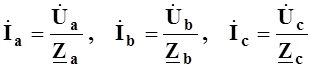,                        (8.5)

где

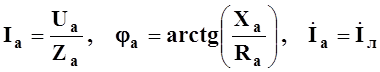
Ток в нейтральном проводе  определяется через токи в фазах по первому закону Кирхгофа для точки n

.                                          (8.6)

Фазные токи при симметричной нагрузке образуют симметричную систему токов, вследствие чего ток  в нейтральном проводе равен нулю.

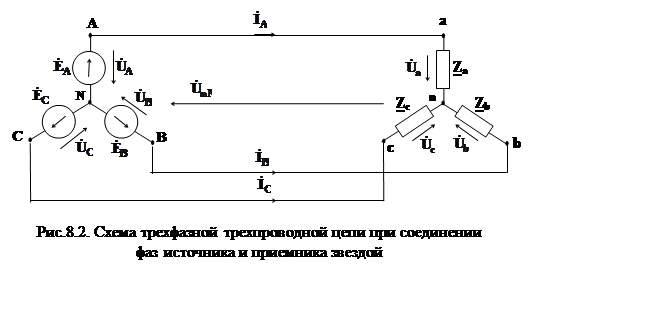При соединении источника и приемника по схеме “звезда-звезда” без нейтрального провода рис.8.2 расчет цепи ничем не отличается от предыдущего случая, если приемник симметричный.

В случае несимметричной нагрузки () симметрия фазных токов нарушается, что приводит к нарушению симметрии фазных напряжений на стороне приемника. Между нейтральными точками n приемника и N источника возникает напряжение , называемое напряжением между нейтралями или напряжением смещения нейтрали.

Из схемы рис.8.2 следует, что  можно определить по методу двух узлов

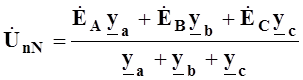,                                    (8.7)

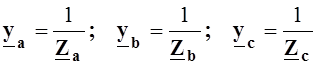где                              (8.8)

- комплексные проводимости фаз приемника.

Записывая уравнения по второму закону Кирхгофа для контуров NАanN, NBbnN, NCcnN можно определить комплексные фазовые напряжения на стороне приемника

               , или

.            (8.9)

Токи в фазах далее определяются по соотношениям (8.5).

При обрыве нейтрального провода схема рис.8.1 совпадает со схемой рис.8.2 и при несимметричной нагрузке расчет ведется по соотношениям (8.7-8.9) и (8.5).

Таким образом, в схеме рис.8.1 нейтральный провод выравнивает фазные напряжения приемника и, следовательно,  в этом случае равно нулю, даже для несимметричного приемника.

При обрыве линейного провода приемники одной фазы остаются без энергии, а приемники двух других фаз получают питание от неповрежденных проводов трехфазной системы. При этом, если имеется нейтральный провод, то обрыв линейного провода для двух других фаз не ощущается, а при отсутствии нейтрального провода две фазы оказываются включенными последовательно на линейное напряжение. При этом фазные напряжения на этих фазах пропорциональны величинам их полных сопротивлений.

1.3. Векторные диаграммы

На рис.8.3 приведены примеры построения векторно-топографических диаграмм напряжений и токов для трех режимов. Диаграмма рис.8.3а отвечает случаю симметричного приемника.

 

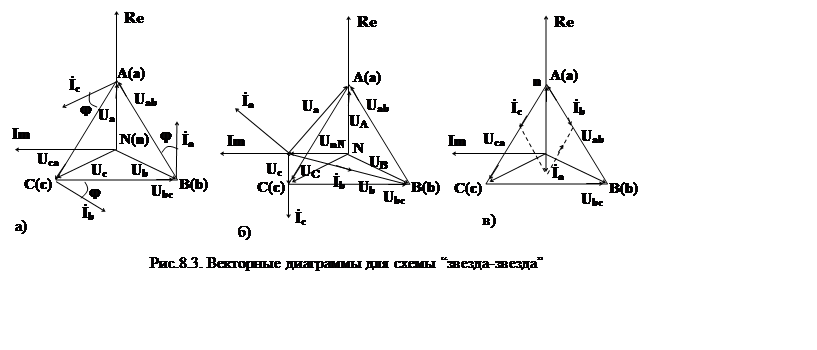
Диаграмма рис.8.3б – для трехпроводной цепи с конденсатором в фазе a. Диаграмма рис.8.3в – для режима короткого замыкания фазы a. (При этом в фазах b и с включены резисторы с одинаковыми сопротивлениями).

1.4. Мощность, потребляемая трехфазной цепью

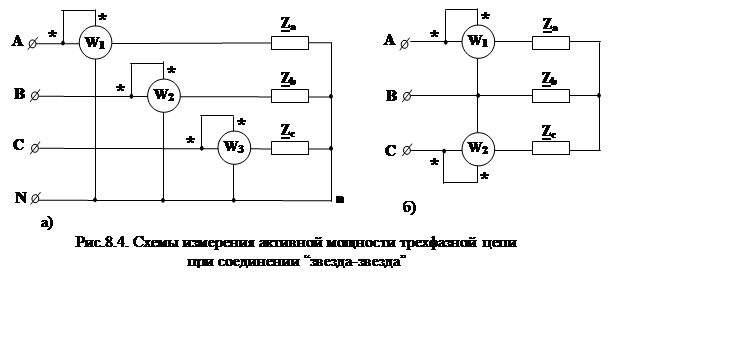
Соотношения для расчета мощности в трехфазной цепи при соединении “звезда-звезда” аналогичны соотношениям для схемы “звезда-треугольник” (см. лабораторную работу N 1.7, раздел 1.4). Для измерения мощности при несимметричном приемнике применяется метод трех ваттметров рис.8.4а, либо метод двух ваттметров рис.8.4б.

 

2. Задание, выполняемое при домашней подготовке

2.1. По конспекту лекций, рекомендуемой литературе и разделу 1 данной работы усвоить основные понятия, определения и величины, характеризующие процессы в трехфазных цепях при соединении источника и приемника по схеме “звезда-звезда”. Изучить методику расчета токов, построения векторных диаграмм, расчета и измерения активной мощности.

2.2. Заготовить отчет по требованиям раздела 5.

3. Лабораторное задание

3.1. С помощью вольтметра проверить разметку зажимов трехфазного блока питания БП4.Определить нейтральную точку N(0) по показаниям вольтметра, поочередно присоединяя вольтметр к каждой паре выходных зажимов. Измерить и записать в таблицу 8.1 значения линейных напряжений на клеммах блока ,  и .