











Лабораторная работа N 1.5
Исследование линейной однофазной электрической цепи синусоидального тока с последовательным соединением элементов
Цель работы:
· исследовать электрическое состояние линейной цепи синусоидального тока при последовательном соединении различных приемников;
· научиться вычислять параметры электрической цепи и строить векторные диаграммы, треугольники напряжений, сопротивлений и мощностей по опытным данным;
· исследовать явление резонанса напряжений и определить параметры последовательного колебательного контура.
1. Краткие теоретические сведения
1.1.
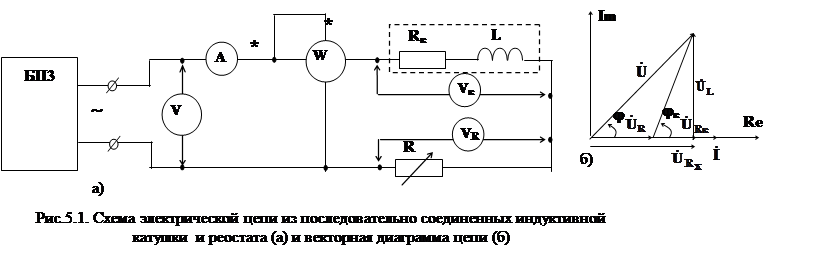
Рассмотрим физические процессы в электрической цепи, состоящей из
последовательно соединенных индуктивной катушки с параметрами ![]() и L и реостата
с регулируемым электрическим сопротивлением R рис.5.1а.
и L и реостата
с регулируемым электрическим сопротивлением R рис.5.1а.
Величина (действующее значение) тока в этой цепи равно
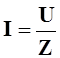 ,
,
где U – действующее значение напряжения на зажимах цепи;
Z – модуль комплекса полного сопротивления,
определяемый выражением ![]() ;
;
![]() - суммарное активное сопротивление цепи;
- суммарное активное сопротивление цепи;
![]() - индуктивное сопротивление катушки;
- индуктивное сопротивление катушки;
w - угловая частота;
f - циклическая частота.
![]() .
(5.1)
.
(5.1)
Если принять начальную фазу тока в цепи ![]() , т.е., принять, что
, т.е., принять, что ![]() , то
, то ![]() , а
, а
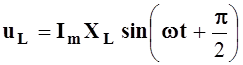 ,
(5.2)
,
(5.2)
и, следовательно,
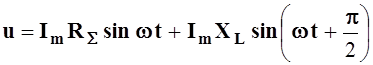 . (5.3)
. (5.3)
Из (5.2) следует, что
напряжение на активном сопротивлении совпадает по фазе с током, а напряжение на
индуктивном элементе опережает на ![]() по фазе ток,
протекающий через этот элемент.
по фазе ток,
протекающий через этот элемент.
![]() ,
(5.4)
,
(5.4)
где ![]() - комплекс действующего
значения напряжения на входе цепи;
- комплекс действующего
значения напряжения на входе цепи;
![]() - комплекс
действующего значения падения напряжения на активной составляющей входного
сопротивления цепи;
- комплекс
действующего значения падения напряжения на активной составляющей входного
сопротивления цепи;
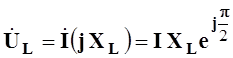 - комплекс действующего значения падения напряжения на
индуктивном элементе.
- комплекс действующего значения падения напряжения на
индуктивном элементе.
Следовательно, уравнение (5.4) можно записать в виде
![]() .
(5.5)
.
(5.5)
Решая (5.5) относительно комплекса тока, получим
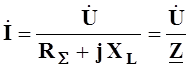 ,
(5.6)
,
(5.6)
где ![]() -
комплекс входного сопротивления цепи рис.5.1а.
-
комплекс входного сопротивления цепи рис.5.1а.
Так
как напряжение ![]() , приложенное от блока питания к
входным зажимам цепи “уравновешивается” векторной суммой напряжений
, приложенное от блока питания к
входным зажимам цепи “уравновешивается” векторной суммой напряжений ![]() и
и ![]() , то
векторную диаграмму цепи рис.5.1б можно построить методом засечек, зная (из
эксперимента) U,
, то
векторную диаграмму цепи рис.5.1б можно построить методом засечек, зная (из
эксперимента) U, ![]() и
и ![]() . На этой диаграмме:
. На этой диаграмме:
j - угол сдвига фаз между напряжением ![]() и током
и током ![]() в цепи
(
в цепи
(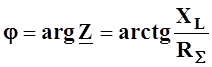 );
); ![]() ;
;
![]() -
угол сдвига фаз между напряжением
-
угол сдвига фаз между напряжением ![]() и током
и током ![]() для катушки индуктивности.
для катушки индуктивности.
Векторы
![]() ,
, ![]() и
и ![]() образуют треугольник напряжений.
образуют треугольник напряжений.
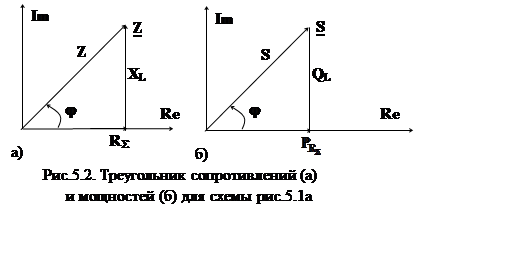 Если каждую из сторон треугольника напряжений
разделить на ток
Если каждую из сторон треугольника напряжений
разделить на ток ![]() , то получим треугольник
сопротивлений рис.5.2а. Умножая стороны треугольника напряжений на ток
, то получим треугольник
сопротивлений рис.5.2а. Умножая стороны треугольника напряжений на ток ![]() , получим треугольник мощностей рис.5.2б.
, получим треугольник мощностей рис.5.2б.
Из треугольника сопротивлений рис.5.2а следуют соотношения
![]() ;
; ![]() ;
; ![]() ;
; 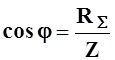 . (5.7)
. (5.7)
Из треугольника мощностей рис.5.2б следуют соотношения
![]() ;
; ![]() ;
; 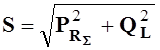 ;
; 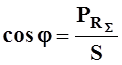 , (5.8)
, (5.8)
где ![]() - комплекс полной
мощности цепи;
- комплекс полной
мощности цепи;
![]() - полная мощность цепи.
- полная мощность цепи.
С учетом закона Ома для действующих величин тока и напряжения, имеют место соотношения
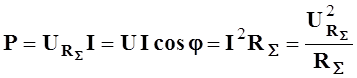 - активная мощность
цепи;
- активная мощность
цепи;
![]() - реактивная мощность
цепи.
- реактивная мощность
цепи.
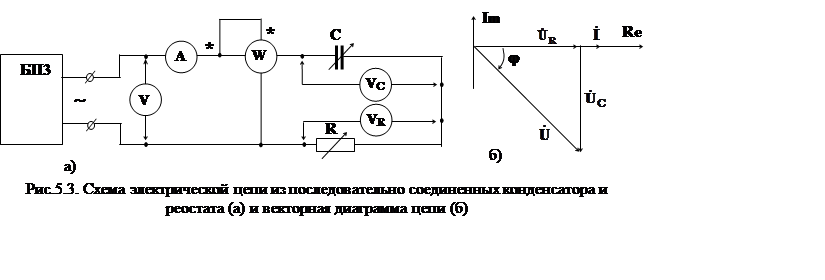
1.2. Рассмотрим аналогично процессы в электрической цепи, состоящей из последовательно соединенных конденсатора с электрической емкостью С и реостата с регулируемым электрическим сопротивлением R рис.5.3а.
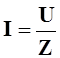 ,
(5.9)
,
(5.9)
где
![]() - модуль комплекса полного сопротивления;
- модуль комплекса полного сопротивления;
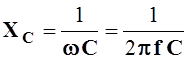 - емкостное сопротивление конденсатора.
- емкостное сопротивление конденсатора.
Согласно второму закону Кирхгофа, уравнение для мгновенных значений напряжений имеет вид
![]() .
(5.10)
.
(5.10)
Если
![]() , то
, то ![]() , а
, а 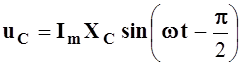 и, следовательно,
и, следовательно,
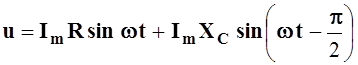 .
(5.11)
.
(5.11)
Следовательно, напряжение на конденсаторе отстает на 90° по фазе от тока, протекающего через него.
Уравнение (5.10) в символической форме имеет вид
![]() ,
(5.12)
,
(5.12)
![]() где
где 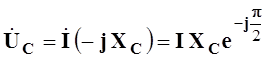 - комплекс
действующего значения падения напряжения на емкостном элементе.
- комплекс
действующего значения падения напряжения на емкостном элементе.
Следовательно, уравнение (5.12) можно записать в виде
![]() , (5.13)
, (5.13)
или
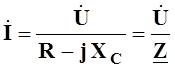 ,
(5.14)
,
(5.14)
где
![]() - комплекс входного сопротивления цепи
рис.5.3а.
- комплекс входного сопротивления цепи
рис.5.3а.
Векторная
диаграмма этой цепи, построенная методом засечек по величинам U,
![]() ,
, ![]() приведена
на рис.5.3б.
приведена
на рис.5.3б.
Угол
j сдвига фаз между напряжением ![]() на
входе цепи и током I в цепи отрицателен и может изменяться в пределах
на
входе цепи и током I в цепи отрицателен и может изменяться в пределах ![]() .
.
Треугольники сопротивлений и мощностей для этой цепи представлены на рис.5.4а,б.
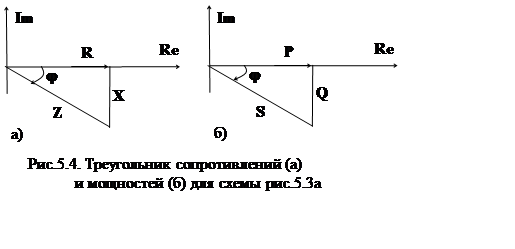 Из этих треугольников, с учетом закона Ома для
действующих значений напряжения и тока следуют соотношения, аналогичные
соотношениям (5.7), (5.8), (5.9). Однако, при этом реактивная мощность отрицательна,
так как
Из этих треугольников, с учетом закона Ома для
действующих значений напряжения и тока следуют соотношения, аналогичные
соотношениям (5.7), (5.8), (5.9). Однако, при этом реактивная мощность отрицательна,
так как ![]() и, следовательно,
и, следовательно, ![]() .
.
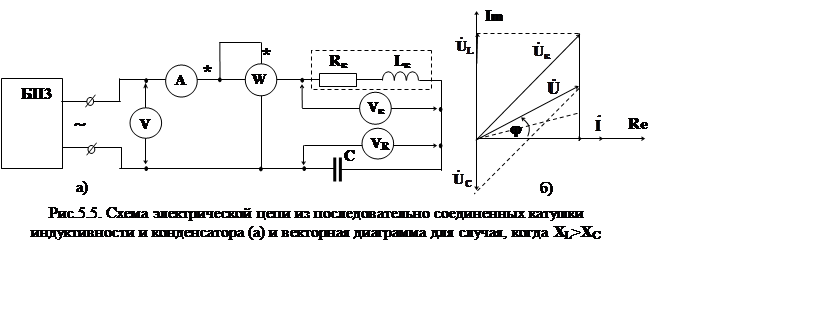 1.3. Рассмотрим схему рис.5.5а с последовательным
соединением катушки индуктивности с параметрами
1.3. Рассмотрим схему рис.5.5а с последовательным
соединением катушки индуктивности с параметрами ![]() ,
, ![]() и конденсатора с электрической емкостью С.
и конденсатора с электрической емкостью С.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.