Исследование линейной однофазной электрической цепи синусоидального тока с последовательным соединением элементов (Лабораторная работа № 1.5), страница 2

Величина тока в этой цепи равна ,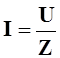

где  - модуль комплекса входного сопротивления цепи рис.5.5а (полное сопротивление цепи);

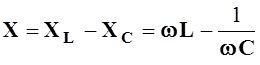        - реактивное сопротивление цепи.

Уравнение для мгновенных значений напряжений согласно второму закону Кирхгофа имеет вид

.                                   (5.15)

Это уравнение, с учетом выражений ; ; 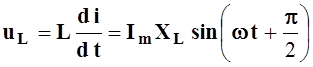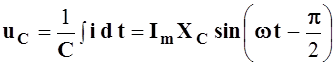, можно представить в виде

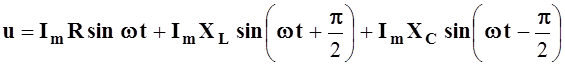.       (5.16)

Из этих выражений следует, что угол j сдвига фаз между напряжением  на входе цепи рис.5.5а и током  в цепи может быть положительным, когда , отрицательным, когда  и  равным нулю, когда .

Действительно, уравнение (5.15) в символической форме записи имеет вид

,                        (5.17)

или

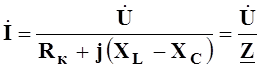,                            (5.18)

где 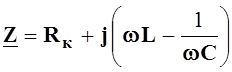- комплекс входного сопротивления цепи рис.5.5а.

Поскольку из (5.18) следует, что

,

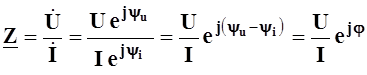то очевидно, что 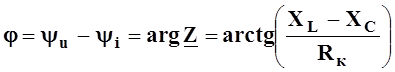, и, следовательно, угол j может быть положительным (), отрицательным () или равным нулю ().

Векторно-топографическая диаграмма напряжений для случая  приведена на рис.5.5б.

Под резонансом напряжений понимают такой режим работы цепи из последовательно соединенных R, L, C-элементов, при котором разность фаз j между напряжением  на входе цепи и током  в этой цепи равна нулю.

Так как 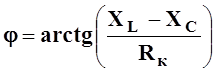, то  выполняется, если  или если 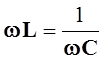, откуда следует, что при заданных         L, C-параметрах резонанс напряжений имеет место на определенной частоте

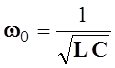,                                                (5.19)

называемой резонансной частотой.

Так как , то

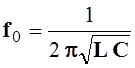.                                            (5.20)

Величины  и  называются угловой и циклической резонансной частотой.

Величины напряжений на реактивных элементах контура рис.5.5а при резонансе в q раз больше, чем величина напряжения U, приложенная к входным клеммам цепи рис.5.5а.

Действительно,

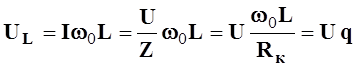,                    (5.21)

где 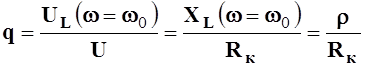  - добротность контура или коэффициент резонанса;

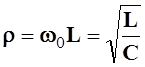          - характеристическое сопротивление контура.

Аналогично,

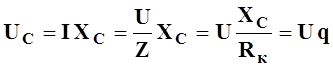,                     (5.22)

где ,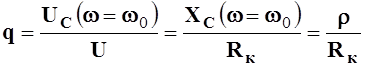

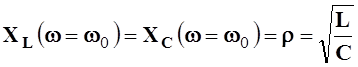.                      (5.23)

Таким образом, под добротностью qпоследовательного контура рис.5.5а понимают отношение характеристического сопротивления 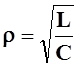 этого контура к его активному сопротивлению R (для схемы рис.5.5а ).

Величина 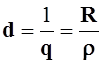 называется затуханием контура.

Комплексная мощность , развиваемая источником ЭДС равна

.                          (5.24)

Активная мощность, потребляемая электрической цепью,

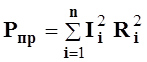.                                         (5.25)

Реактивная мощность цепи равна

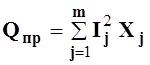,                                        (5.26)

где слагаемые  для индуктивных элементов и <0 – для емкостных.

Таким образом, баланс активной мощности выражается соотношением

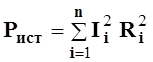, где n – число резисторов в цепи, а баланс реактивной мощности

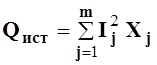, где m– число реактивных элементов в цепи.

2. Задание, выполняемое при домашней подготовке

2.1. По конспекту лекций, рекомендуемой литературе [1-4] и разделу 1 данной работы изучить величины, применяемые при анализе процессов в линейных цепях синусоидального тока, особенности записи уравнений по закону Ома и законам Кирхгофа для мгновенных величин и в символической форме. Научиться строить векторно-топографические диаграммы напряжений, треугольники напряжений, сопротивлений и мощностей. Изучить явление резонанса напряжений, методы расчета и измерения параметров последовательного колебательного контура.

2.2. Для схемы рис.5.1а записать выражения для расчета величин Z, , R, , , , , L,  по заданным (экспериментальным) данным I, U, , , Pи f.

2.3. Для схемы рис.5.3а записать выражения для расчета величин Z, R, ,  и С, если заданы величины I, U, , , P и f.

2.4. Для схемы рис.5.5а записать выражения для расчета величин Z, , X, , , , L,  и С, если заданы величины I, U, , , P и f.

2.5. Для схемы рис.5.5а записать выражения для I, , , P,  как функции величины изменяющейся емкости С конденсатора, считая заданными величинами U, , , w и С.

2.6. Заготовить отчет по требованиям раздела 5.

3. Лабораторное задание

3.1. Собрать электрическую цепь по схеме рис.5.1а, подсоединив ее входные зажимы  к клеммам блока питания БП3 и установить величину напряжения U на входе цепи, заданную преподавателем. Изменением сопротивления Rреостата установить величину тока в цепи в пределах 0,5-0,7 А. Измерить и записать в таблицу 5.1 значения величин I, U, U_C, U_к, Р.

Таблица 5.1

Данные измерений

Результаты вычислений

Для всей цепи

Для индуктивной катушки

Для резистора

U

Uк

UR

I

P

Z

RS

cosj

j

Zк

Rк

XL

L

cosjк

jк

R

В

В

В

А

Вт

Ом

Ом

-

град

Ом

Ом

Ом

Гн

град

Ом