Звіти по індивідуальних розрахунково-аналітичних завданнях № 1-8 (Зведення та групування статистичних даних. Вибірковий метод)

ІНДИВІДУАЛЬНЕ РОЗРАХУНКОВО-АНАЛІТИЧНЕ ЗАВДАННЯ № 1

За темою «Зведення та групування статистичних даних»

1. За наведеними в таблиці 2 (для варіанта 3) статистичними даними  проведемо групування робітників окремо за кожною з ознак

а)   виробничого стажу роботи, років;

б)   розряд;

в)   середній рівень другої ознаки.

а) групування робітників за виробничим стажем.

Для визначення структури чисельності робітників за виробничим стажем роботи побудуємо інтервальний ряд розподілу. Розмір інтервалу визначимо за формулою 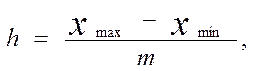1.1:

                                             (1.1)

де – найбільше і найменше значення ознаки;

– кількість груп.

Відповідно m (за табличкою В.К. Горкового = 6, т. як N = 40), тоді  = 23 роки, = 0 років.

h = ( 23 – 0) : 6 = 3,83 років. Побудуємо розрахункову таблицю 1.1.

Таблиця 1.1

№ групи	Вироб. стаж роботи, р.	Кількість робітників ( їх номер)	Разом
І	0 – 3,83	2, 4, 5, 9, 11, 12, 14, 17, 18, 19, 22, 28, 30, 31, 33, 34, 37	17
ІІ	3,83 – 7,66	1, 3, 6, 10, 13, 15, 20, 21, 25, 26, 27, 32, 39	13
ІІІ	7,66 – 11,49	7, 8, 16, 23, 29, 35, 40	7
IV	11,49 – 15,32	24	1
V	15,32 – 19,15	36	1
VI	19,15 – 23	38	1
Разом		40	40

Висновок: найбільше працівників мають виробничий стаж роботи у межах від 0 до 3,83 років.

б) та. як розряд не є інтервальною величиною, побудуємо групування для розряду таким чином:

Таблиця 1.2

№ з/п	Розряд	Кількість робітників (їх номери)	Разом
І	1	2,5,14,19,22,30,37	7
ІІ	2	4,6,9,11,12.17,18,21,25,28,32,34,37	13
ІІІ	3	7,10,15,16,26,27,29,35,39,40	10
IV	4	1,3,20,23,24,31	6
V	5	8,13,36	3
VI	6	38	1
Разом		40	40

Висновок: найбільше робітників на підприємстві мають розряд 2.

в)   середній рівень другої ознаки визначимо за допомогою ділення суми розряду на кількість робітників у кожної з груп. Для кінцевих розрахунків побудуємо розрахункову таблицю 1.3.

Таблиця 1.3

№ групи	Вир. стаж роботи, років	К-ть робітників	Сума розряду робітників,грн	Середній розряд
ІІ	0 – 3,83	17	29	1,71
ІІІ	3,83 – 7,66	13	40	3,08
IV	7,66 – 11,49	7	24	3,43
V	11,49 – 15,32	1	4	4
VI	15,32 – 19,15	1	5	5
ІІ	19,15 – 23	1	6	6
Разом		40	108

Висновок: якщо виробничий стаж роботи високий, то, відповідно і розряд найвищий.

2.  Комбінаційне групування за двома ознаками. Для цього групування побудуємо розрахункову таблицю 1.4.

Таблиця 1.4

Вироб. стаж роботи, років	Розряд						Разом
	1	2	3	4	5	6
0 – 3,83	2,5,14,19,22, 30,33	4,9,11,12, 17,18,28,34,37	____	31	____	____	17
3,83 – 7,66	____	6,21,25,32	10,15,26,27,39	1,3,20	13	____	13
7,66 – 11,49	____	____	7,16,29,35,40	23	8	____	7
11,49 – 15,32	____	____	____	24	____	____	1
15,32 – 19,15	____	____	____	____	36	____	1
19,15 – 23	____	____	____	____		38	1
Разом	7	13	10	6	3	1	40

Висновок: Зі збільшенням виробничого стажу роботи збільшується розряд робітників, і навпаки.

ІНДИВІДУАЛЬНЕ РОЗРАХУНКОВО-АНАЛІТИЧНЕ ЗАВДАННЯ № 2

За темою «Аналіз рядів розподілу»

1.   Характеристики центру розподілу (середню, моду і медіану) для кожної з

ознак:

а)   виробничий стаж роботи, років

б)   розряд

а) побудуємо таблицю, де знайдемо центр інтервалу за формулою 2.1 середнього значення інтервалу:

(2.1)

де – найбільше і найменше значення ознаки.

Побудуємо розрахункову таблицю 2.1.

Таблиця 2.1

Виробничий стаж роботи, р.	Виробничий стаж роботи, років	К-ть робітників
0 – 3,83	1,915	17
3,83 – 7,66	5,745	13
7,66 – 11,49	9,575	7
11,49 – 15,32	13,405	1
15,32 – 19,15	17,235	1
19,15 – 23	21,075	1
Разом		40

1.1. Знайдемо середній виробничий стаж роботи, використовуючи формулу 2.2 середньої арифметичної зваженої:

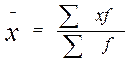;                                                                (2.2)

 де  -  окреме значення досліджуваної ознаки (заробіток робітника);

-  кількістьодиниць, що володіють даним значенням ознаки.

Таким чином середній виробничий стаж дорівнює:

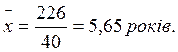
Отже, середній виробничий стаж роботи одного робітника = 5,65 років.

1.2. Знайдемо моду виробничого стажу роботи за формулою 2.3:

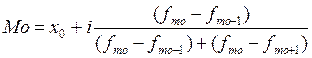,                                   (2.3)

де x₀ – нижня межа модального інтервалу;

i – величина інтервалу;

f _mo– частота модального інтервалу;

f_mo-1 – частота інтервалу, що передує модальному;

f_mo+1 – частота позамодального інтервалу (того, що йде після модального інтервалу).

У даному випадку:

x₀  = 0; i = 3,83; f _mo = 17;  f_mo-1 = 0;  f_mo+1 =13.

Мода виробничого стажу роботи дорівнює:

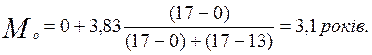
Отже, модою буде 3,1 років виробничого стажу, т. як цьому значенню варіанти відповідає найбільше число робітників (частота).

1.3.  Знайдемо медіану виробничого стажу роботи за формулою 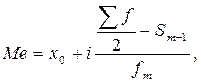2.4:

                                                (2.4)

де x₀ – це нижня межа медіанного інтервалу;

 i – величина інтервалу;

S_m-1 – сума накопичених частот до медіанного інтервалу;

f_m – частота медіанного інтервалу.

У даному випадку:

x₀ = 3,83; i = 3,83; S_m-1 = 17; f_m = 13.

Медіана виробничого стажу роботи дорівнює:

Отже, половина робітників має менш ніж 4,71 років виробничого стажу, а друга половина – більше.

1.4.  Знайдемо середній розряд за формулою 2.2:

Середній розряд приблизно дорівнює 3.

1.5.  Визначимо моду розряду. Т. як розряд не інтервальний, то мода – ознака,я ка має найбільшу частоту. Тому модою буде 2, тому що найбільше число робітників мають 2-гий розряд.

1.6.   Визначимо медіану розряду за формулою:

Медіана дорівнюватиме 3,5. Отже, половина робітників має розряд менш, ніж 3,5, а друга половина – більше.

2.   Абсолютні та відносні показники варіації (розмах варіації, середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення, лінійний та квадратичний коефіцієнт варіації).

2.1. Розмах варіації визначимо за формулою 2.5:

R = χ_max - χ_min,                                                                                         (2.5)

а)   розмах варіації виробничого стажу дорівнює:

R = 23 – 0 = 23 роки.

б)  розмах варіації розряду дорівнює:

R = 6 – 1 = 5.

2.2. Знайдемо середнє лінійне відхилення за формулою 2.6:

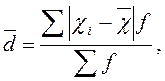
(2.6)

2.3. Знайдемо дисперсію за формулою 2.7:

                                             (2.7)

2.4. Знайдемо середнє квадратичне відхилення за формулою 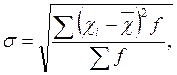2.8:

                                                 (2.8)

2.5.  Знайдемо коефіцієнти варіації (лінійний та квадратичний) відповідно за формулами 2.9 та 2.10:

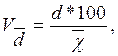                          (2.9) 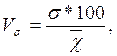                                                                  (2.10)

Побудуємо для зручності розрахунків показників варіації для виробничого стажу роботи  таблицю 2.3.

Таблиця 2.3

В. стаж роботи, р.	К-ть робітників
1,915	17	3,735	13,95023	63,495	237,1538
5,745	13	0,095	0,009025	1,235	0,117325
9,575	7	3,925	15,40563	27,475	107,8394
13,405	1	7,755	60,14003	7,755	60,14003
17,235	1	11,585	134,2122	11,585	134,2122
21,075	1	15,425	237,9306	15,425	237,9306
Разом	40			126,97	777,3934

За наведеними даними розрахуймо середнє лінійне відхилення за формулою 2.6:

Дисперсія (середній квадрат відхилення) за формулою 2.7 дорівнює:

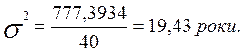
Середнє квадратичне відхилення відповідно за формулою 2.8 дорівнює:

Коефіцієнти варіації (лінійний та квадратичний) відповідно за формулами 2.9 та 2.10 дорівнюють:

                                                                  

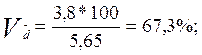
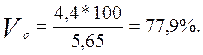
Висновок: отже, стаж роботи окремих робітників відрізняється від середнього показника на 3,8 за середнім лінійним відхиленням та на 4,4 за середнім квадратичним відхиленням. Коефіцієнт варіації 77,9% свідчить  про значні коливання стажу роботи окремих робітників по відношенню до середнього стажу роботи на підприємстві, а це означає, що сукупність робітників підприємства за стажем роботи не можна вважати якісно однорідною.

б)  аналогічно знайдемо данні показники для розряду. Побудуємо розрахункову таблицю 2.4.

Таблиця 2.4

Розряд	К-ть робітників
1	7	1,7	11,9	2,89	20,23
2	13	0,7	9,1	0,49	6,37
3	10	0,3	3	0,09	0,9
4	6	1,3	7,8	1,69	10,14
5	3	2,3	6,9	5,29	15,87
6	1	3,3	3,3	10,89	10,89
Разом	40		42	21,34	64,4

За наведеними даними розрахуймо середнє лінійне відхилення за формулою 2.6:

Дисперсія (середній квадрат відхилення) за формулою 2.7 дорівнює:

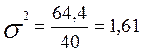
Середнє квадратичне відхилення відповідно за формулою 2.8 дорівнює:

Коефіцієнти варіації (лінійний та квадратичний) відповідно за формулами 2.9 та 2.10 дорівнюють:

                                                               

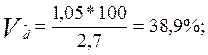
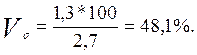
Висновок: отже, розряд окремих робітників відрізняється від середнього показника на 1,05 за середнім лінійним відхиленням та на 1,3 за середнім квадратичним