Экономика и менеджмент \ Статистика

Аналіз інтенсивності динаміки. Аналіз тенденції розвитку коливань. Індексний метод

Страницы работы

46 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Водночас, відмітимо, що теоретична лінія, що вирівнює ряд динаміки цілком залежить тільки від двох значень рівнів ряду (початкового і кінцевого), які можуть зазнавати істотних випадкових коливань. У зв’язку з цим, прийоми доцільно використовувати лише для рядів, що мають дані стабільні щорічні прирости.

Найбільш ефективним способом виявлення основної тенденції є аналітичне вирівнювання. Вирівнювання за прямою використовується в тих випадках, коли абсолютні прирости більш-менш постійні, тобто коли рівні динамічного ряду змінюються в арифметичній прогресії, або близькі до неї.

Процес аналітичного вирівнювання складається з двох етапів:

– відбір типу кривої, форма якої відповідає тренду ряду динаміки;

– визначення чисельних значень (оцінювання) параметрів кривої на знаходження теоретичних рівнів ряду динаміки.

Питання про вибір типу кривої є головним як при вирівнюванні ряду, так і при подальшому прогнозуванні. На практиці для моделювання методом аналітичного вирівнювання використовується 10-15 найпростіших функцій (рівнянь тренду). Визначення конкретного рівняння, яке використовується для подальшого вирівнювання ряду та прогнозування, здійснюється двома шляхами: а) шляхом аналізу графіку ряду динаміки з метою визначення функції, яка йому наближено відповідає; б) на основі статистичних критеріїв, які характеризують відхилення емпіричного ряду від апроксимуючої функції.

Для аналітичного вирівнювання найчастіше використовують такі функції:

Функція	Формула	Умови застосування
лінійна		використовується в тому випадку, якщо абсолютні прирости більш-менш рівномірні	– вирівняні (розрахункові) рівні ряду динаміки; а₀, а₁ – параметри рівняння; t – номер року.
параболічна (парабола)		використовується в тому випадку, якщо абсолютні прирости рядів динаміки не стабільні, а мають тенденцію до зростання або зниження
степенева	y_t=a_0a₁^t*	використовується в тому випадку, якщо ланцюгові коефіцієнти зростання приблизно постійні
гіпербола		використовується в тому випадку, якщо виявлено уповільнене зниження (зростання) рівнів ряду, які за логікою не можуть знизитися до нуля

У зазначених функціях t — порядковий номер періоду (дати), а — рівень ряду при t = 0. Параметр b характеризує швидкість динаміки: середню абсолютну в лінійній функції і середню відносну — в експоненті. Коли характеристики швидкості розвитку зростають (чи зменшуються), використовуються інші функції (парабола 2-го степеня, модифікована експонента тощо).

Параметри рівнянь для аналітичного вирівнювання:

Назва функції	лінійна	параболічна (парабола)
Вигляд функції
Система рівнянь параметрів рівняння (за умови ∑t = 0)
∑у – сума рівнів ряду динаміки; а₀, , – параметри регресії; п – кількість рівнів ряду динаміки; – порядковий номер року.
Система рівнянь спрощується, якщо початок відліку часу (t = 0) перенести в середину динамічного ряду. Тоді значення t, розміщені вище середини, будуть від’ємними, а нижче — додатними. При непарнoму числі членів ряду (наприклад, n = 5) змінній t надаються значення з інтервалом одиниця: –2, –1, 0, 1, 2; при парному: –2,5, –1,5, –0,5, 0,5, 1,5, 2,5. В обох випадках , а система рівнянь набирає вигляду , . Отже, .

Щоб оцінити ступінь наближення лінійного тренду до фактичних даних динамічного ряду, визначаємо середнє квадратичне відхилення і коефіцієнт варіації.

Назва показника

Формула

Умовні позначення

Залишкове середнє квадратичне відхилення (σ_s)

– розрахункові рівні ряду динаміки;

у – фактичні рівні ряду динаміки;

п – кількість рівнів ряду динаміки.

Коефіцієнт варіації (квадратичний)

– середнє квадратичне відхилення;

– середнє значення досліджуваної ознаки.

Суми фактичних рівнів і розрахованих за лінійним трендом теоретичних рівнів

однакові:

Методика вирівнювання ряду динаміки за прямою

Є дані про видобуток нафти за п’ять років (дані на початок року):

Рік	2009	2010	2011	2012	2013
Видобуток нафти, млн. т	72	110	95	135	120

Визначити лінію тренда і, використовуючи одержане рівняння,зробити прогноз на 2016 рік.

Розв’язок

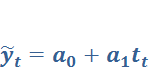Припустимо, що видобуток нафти змінюється за прямою , оскільки динаміка характеризується стабільним абсолютним приростом (+6, +5, +4, +3);

де а₀, – параметри регресії; – порядковий номер року.

Невідомі параметри а₀, визначають методом найменших квадратів, розв’язуючи систему нормальних рівнянь:

де ∑у – сума рівнів ряду динаміки;

а₀, – параметри регресії;

п – кількість рівнів ряду динаміки;

– порядковий номер року.

Побудуємо розрахункову таблицю для розв’язання системи рівнянь.

Рік	, млн т	Умовна ознака часу, t	t²	y_tt	= 70,1 + 12,1t
2009	72	1	1	72	82,2
2010	110	2	4	220	94,3
2011	95	3	9	285	106,4
2012	135	4	16	540	118,5
2013	120	5	25	600	130,6
Разом	532	15	55	1717	532