Программируемые логические матрицы, страница 4

Для расширенных ПЛМ (s, t, q) по  выходам в К раз достаточно соединить одноимённые входы К ПЛМ.

Пример расширенной ПЛМ приведён на рис. 27.5а.

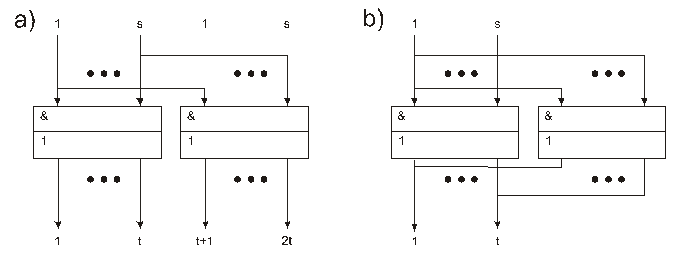
Рисунок 27.5 – Расширение ПЛМ по выходам (а) и по термам (b)

Полученная схема (рис. 27.5) эквивалентна ПЛМ с параметрами s, t, q ,r. Матрица М₁ у всех К ПЛМ совпадают, а матрица М₂ всех ПЛМ (s, t, q) позволяют реализовать систему из Kt функций от S переменных с q термами.

При расширении ПЛМ (s, t, q) по термам в К раз необходимо соединить как одиночные входы, так и одноимённые выходы всех К ПЛМ (s, t, q). При этом выходы соединяются с помощью логических схем ИЛИ. В общем случае при расширении ПЛМ по термам в К раз потребуется t логических схем ИЛИ с К входами в каждую. Однако в настоящее время выпускаются ПЛМ, выходы которых при расширении по термам можно соединить непосредственно (рис. 5в).

При расширении ПЛМ (s, t, q) по термам в К раз матрицы М₁ всех К ПЛМ реализуют Kq различных термов, которые могут быть использованы в ДНФ любой из t функций.

Построение на ПЛМ (s, t, q) системы булевых функций от переменных, число L которых превышает число S входов в ПЛМ, и реализации автомата с  входными переменными и H>q переходами на ПЛМ (s, t, q ,r) не так тривиальны и основаны на методах декомпозиции булевых функций и автоматов.