Системы секвенций и формул перехода, страница 2

Таблица 24.1

24.2 Приведение формул перехода к скобочной форме

            Представление формулы перехода в виде:

,                                             (24.5)

            где xlÎ{x1,…,xL}, а A и B подформулы перехода не зависящие от xl. Носит  название приведения формулы перехода по переменной Xi.

Если какие-то члены формулы перехода не зависят от xl, то при приведении по Xi необходимо их предварительно умножить на выражение   . Таким образом любая формула перехода может быть разложена по любой входящей в нее переменной.

Для примера рассмотрим формулу перехода:

      (24.6)

 Например, после преведения формулы (24.6) по переменной x2 получим:

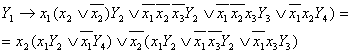        (24.7)

В выражении (24.5) можно продолжить приведение подформул А,В по другим переменным до тех пор, пока во внутренних скобках не окажутся выражения вида:

,                                   (24.8)

где xpÎ{x1,…,xL}, Ym, YnÎ{Y1,…,YT+1}.

            Полученная формула перехода называется скобочной формулой перехода и система таких формул - системой скобочных формул перехода. Выражения вида (24.8) называются элементарными.

            Представление формулы (24.7) в скобочной форме (24.9):

                (24.9)

После представления алгоритма система скобочных формул перехода легко получить ГС.

            Ясно, что каждому выражению типа (24.8) соответствует подграф, изображенный на рис. 24.1

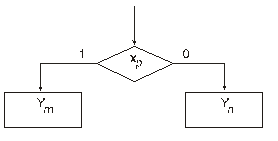
Рис. 24.1 - Подграф соответствующий выражению (24.8)

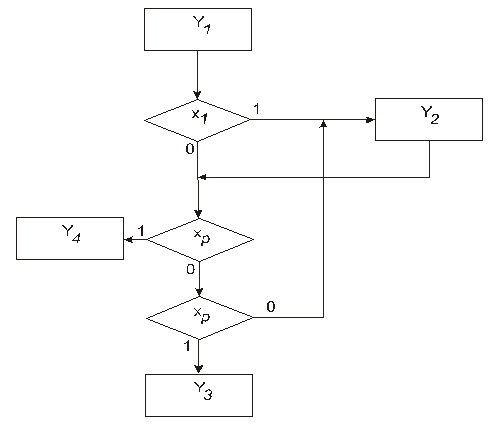
Подграф соответсвующий формуле (24.10) представлен на рис. 24.2.

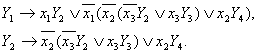(24.10)