24 СИСТЕМЫ СЕКВЕНЦИЙ И ФОРМУЛ ПЕРЕХОДА
24.1 Системы секвенций
В общем случае, оператор Yt сложного алгоритма (описывающего, например, функционирование автоматизированной системы управления (АСУ)) зависит от конечного числа логических условий {xi1,…,xir} принадлежащих множеству X.
В связи с этим, удобно использовать специализированный язык для задания алгоритмов. К числу таких языков относится система секвенций.
Элементарная секвенция определяет условие перехода к оператору последователю Yj после оператора предшественника Yi. Секвенция представлена в форме (24.1):
![]() (24.1)
(24.1)
Символ
![]() означает
“если - то”. Тогда формулу (24.1) следует понимать таким образом: оператор Yj
будет выполнен после оператора Yi если условие
означает
“если - то”. Тогда формулу (24.1) следует понимать таким образом: оператор Yj
будет выполнен после оператора Yi если условие ![]() будет истинно.
будет истинно.
Если оператор Yj имеет множество операторов- предшественников, то секвенция представляется в форме системы секвенций:
![]() , j=1,…,T. (24.2)
, j=1,…,T. (24.2)
Пример алгоритма, представленного в форме системы секвенций :
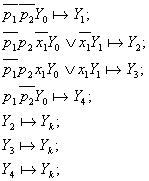 (24.3)
(24.3)
Легко заметить, что систему секвенций можно получить из МСА (таб. 24.1).
Представление алгоритма в форме системы секвенций имеет в качестве преимущества компактность представления. То системы секвенций можно перейти к МСА и далее к другим формам представления алгоритма - граф-схем алгоритма (ГСА), логической схеме алгоритма (ЛСА) или к системе формул перехода (СФП).
|
МСА |
Y1 |
Y2 |
Y3 |
Y4 |
Yk |
|
Y0 |
|
|
|
|
|
|
Y1 |
|
|
|||
|
Y2 |
1 |
||||
|
Y3 |
1 |
||||
|
Y4 |
1 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.