Теория надежности: Методические указания к практическим занятиям

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО ВЫСШЕМУ ОБРАЗОВАНИЮ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ТЕОРИЯ НАДЕЖНОСТИ

Методические указания к практическим занятиям по курсу

"Теория надежности" для студентов 4 курса ДО и

студентов 5 курса ВО АВТФ специальности 22.02.00

Новосибирск-2002

 Данные методические  указания  предназначены  для  проведения практических занятий по курсу "Надежность систем" для студентов 4 курса дневного отделения и 5 курса вечернего отделения АВТФ специальности 22.02.00. Методические указания содержат краткие теоретические положе-

ния и  задачи по расчету основных количественных характеристик элементов и сложных систем с помощью различных математических методов.

 Составил   к.п.н., доцент.  Н.И.Лыгина

  Рецензент

  Работа подготовлена на кафедре АСУ

ВВЕДЕНИЕ

     Одним из  основных вопросов теории надежности является вопрос определения количественных показателей надежности  элементов  и  систем. Для определения надежности элемента или системы прежде всего используется аппарат теории вероятностей.

     В связи  с  этим  в  первой главе методических указаний приведены  краткие сведения из алгебры событий, которая и используется для расчета надежности.

     Во второй главе методических указаний вводятся основные количественные  показатели надеж- ности элементов в вероятностной и статистической формах,  а также рассматриваются показатели  надежности  элементов при  определенном законе распределения времени безотказной работы эле-

мента.

     В третьей главе рассматриваются методы определения основных показателей надежности слож- ных  невосстанавливаемых,  восстанавливаемых  и резервированных  систем,  а  также систем , эле- менты которых могут находиться в трех состояниях .Основное внимание в теоретическом введении  к главе  уделено  методам  структурной  надежности и методу интегральных уравнений.  Метод ин- тегральных уравнений дает  возможность  определить  надежность любой системы. Кроме того для эффективного решения некоторых  задач этой главы предполагается использование метода  диффе- ренциальных  уравнений.  В  каждой  задаче  предварительно необходимо выбрать метод  расчета надежности системы из числа рассмотренных в курсе  "Надежность систем".  Если  возможно ,то расчет надежности системы выполняется несколькими методами.

1. ИСПОЛЬЗОВАНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ ДЛЯ РАСЧЕТА НАДЕЖНОСТИ.

1.1. Алгебра событий .Формула Байеса.

Основными в  теории вероятностей являются косвенные методы вычисления вероятностей.  Этим целям служит так называемая  алгебра событий . Для событий вводятся понятия "сумма событий" ,  " произведение событий" . а также правила действий с событиями .Эти понятия вводятся только  тогда, когда события, о которых идет речь ,представляют собой подмножество одного и того же пространства элементарных событий  W .

   1. Правила сложения вероятностей.

                                       Р ( А + В ) = Р ( А ) + Р ( В ).

Правило сложения легко обобщается на случай произвольного числа  n  несовместных событий :  если               А_i* A_j = 0              при  i-j  , то

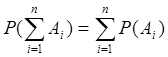
   2. Правила умножения вероятностей.

                                      Р ( А В ) = Р ( А ) * Р ( В /А )

       или, если в качестве первого события взять В,

                                      Р ( А В ) = Р ( В ) * Р ( А/ В ).

Из предыдущей формулы вытекает следующее выражение для условной вероятности  : 

                                      Р ( В /А ) = Р ( А В ) / Р ( А )

Для двух независимых событий правило умножения вероятностей принимает вид

                                      Р ( А В ) = Р ( А ) * Р ( В ).

Несколько событий называются 1 независимыми в совокупности 0 (или просто независимыми), если появление любого числа из них не меняет вероятностей остальных событий. Для нескольких независимых событий правило умножения принимает вид

                                     Р (A₁,A₂, …A_n) = Р ( А₁ ) * Р ( А ₂ )... Р ( А_n ).

     Следствием правил сложения и умножения вероятностей является теорема о повторении опытов,  состоящая в следующем. Если производится n  независимых опытов, в каждом из которых событие  А появляется с вероятностью р, то вероятность того, что в данной серии опытов событие А появля -ется  ровно m  раз, выражается формулой

или, обозначая 1-р=q,

     Вероятность того,  что в серии из n независимых опытов событие  А появляется не менее m раз, выражается формулой

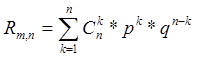
или же

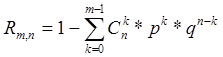
Из двух последних формул выбирают ту, которая содержит меньше членов