Кратчайшие пути из одной вершины. Кратчайшие пути в ациклическом ориентированном графе

Кратчайшие пути из одной вершины.

Задача нахождения кратчайших путей из одной вершины ко всем остальным вершинам решается алгоритмом поиска в ширину для ориентированных и неориентированных графов. Алгоритм строит дерево поиска в ширину, которое перечисляет вершины в порядке возрастания длины путей от исходной вершины. Но этот алгоритм не учитывает весов ребер. Если же на  графе задана весовая функция ребер, то длина путей оценивается не качеством ребер, а суммарным весом пути.

Рассмотрим  задачу нахождения кратчайших путей для ориентированного взвешенного графа G=(V, E) с вещественной весовой функцией w: EàR. Весом пути p=(v₀, v₁,..., v_k) является сумма весов ребер входящих в этот путь

.

Вес кратчайшего пути из вершины uв вершину v равен :

Кратчайший путь из u в v, то любой путь p из u в v, для которого w(p)=d(u, v)

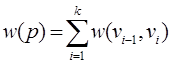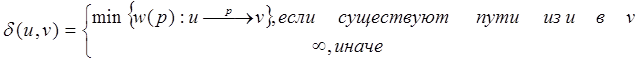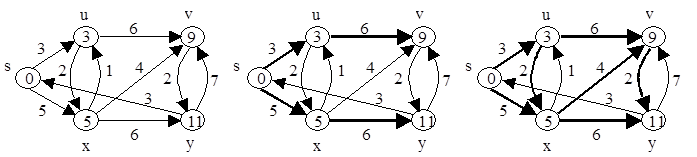В различных задачах весами могут быть длины, времена, стоимости, штрафы, убытки и т. д., т. е. любые величины, обладающие свойством аддитивности. Алгоритм поиска кратчайших путей во взвешенном графе применим во многих задачах.

-  В задачах поиска кратчайших путей в одну вершину. Задача решается поиском кратчайших путей из этой вершины не транспонированном  графе.

-  В задачах поиска кратчайшего пути между заданной парой вершин. Алгоритма, более эффективного, чем алгоритм поиска всех кратчайших путей не существует.

-  В задачах поиска кратчайших путей для всех пар вершин.

В задаче поиска кратчайших путей нужно найти не веса кратчайших путей, а сами пути. Для этого используется тот же прием, что и при построении дерева поиска  в ширину. Для каждой вершины на кратчайшем пути фиксируется ее предшественник p[v] и вес пути от исходной вершины d[v].

Задача поиска кратчайших путей имеет ограничения. Задача не имеет решения, если при построении кратчайшего пути встретился цикл с отрицательным весом. Это возможно если на орграфе задана весовая функция с отрицательными весами ребер. В этом случае по такому циклу можно проходить бесконечно при постоянном уменьшении веса кратчайшего пути.

Если цикл имеет положительный вес, то его можно отбросить из рассмотрения, т. к. это не увеличит веса кратчайшего пути.

Существует несколько алгоритмов поиска кратчайших путей из заданной вершины во взвешенном орграфе. Алгоритм Дейкстры решает задачу для орграфа с неотрицательными весами. Алгоритм Беллмана - Форда, допускает ребра с отрицательным весом и обнаруживает циклы с отрицательным весом. Есть и другие специфические алгоритмы для специальных видов графов.

Все алгоритмы основываются на приеме, называемом релаксацией ребер, которая заключается в постепенном уточнении верхней границы веса кратчайшего пути для каждой вершины.

Для каждой вершины vÎV хранится некоторое число d[v], являющееся верхней оценкой веса кратчайшего пути изSв v. Изначально d[v]=¥. Изначально необходимо инициализировать все вершины:

Initialize_Singlr_Source(G, S)

1.  for (для) всех вершин vÎV[G]

2.      do d[v] ← ¥

3.                  p[v] ←NIL

4.  d[s] ←0

Релаксация ребра (u, v)ÎE состоит в следующем: d[v] уменьшается до d[u] + w(u,v), если эта сумма меньше d[v]. Новое значение становится верхней оценкой кратчайшего пути, а вершина uстановится родителем вершины v, т. е. p[v] ←u

Relax (u, v, w)

1. if d[v] > d[u] + w(u,v)
2.     then d[v] ← d[u] + w(u, v)
3.             p[v] ← u

Свойства релаксации утверждается несколькими леммами:

1.  Пусть G=(V, E) взвешенный орграф с весовой функцией w: EàR и пусть (u, v)ÎE. Тогда сразу же после релаксации этого ребра (вызова Relax(u, v, w) выполняется неравенство:   d[v] £ d[u]+w(u, v))

2.  Пусть G=(V, E) взвешенный орграф с весовой функцией w; пусть SÎV - начальная вершина. Тогда после выполнения процедуры Initialize_Single_Source(G, S), а затем произвольной последовательности операций релаксации ребер для каждой вершины vÎV выполнено неравенство d[v] ³ d(S, v). Если при этом для какой- то из вершин v d[v] = d(S, v). Если при этом для какой-то из вершин v d[v] = d(S, v), то при последующих релаксациях оно сохраняется.

3.  Пусть G=(V, E) взвешенный орграф с весовой функцией w и исходной вершиной S. Пусть вершина vÎV недостижима из S. Тогда после выполнения процедуры Initialize_Single_Source(G, S) и любой последовательности релаксации ребер значение d[v] останется бесконечным.

4.  Пусть G=(V, E) взвешенный орграф с весовой функцией w и исходной вершиной S. Пусть    s              uàv кратчайший путь с последним ребром (u, v). Пусть выполнена процедура Initialize_Single_Source(G, S) и затем - последовательность релаксации  некоторых ребер, включающая релаксацию ребра(u, v). Если в какой - то момент до релаксации ребра (u, v) выполнялось равенство d[u] =d(s, u), то в любой момент после релаксации (u, v) будет выполнено равенство d[v]=d(S, v).

Алгоритм Дейкстры.

Алгоритм Дейкстры решает задачу  о кратчайших путях из одной вершины для взвешенного орграфа G=(V, E) с исходной вершиной S, в котором веса ребер неотрицательны.