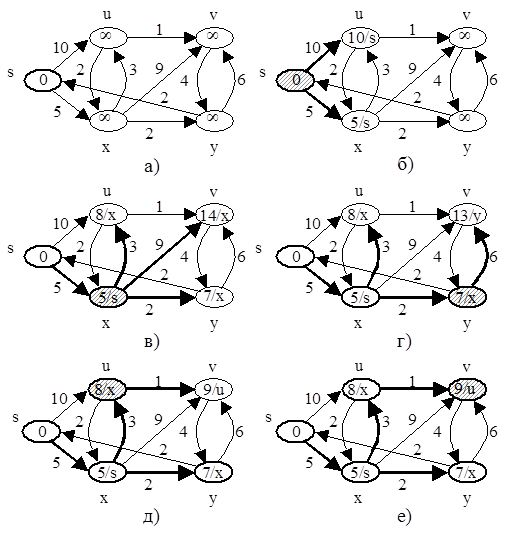
Информатика и выч. техника \ Структуры и алгоритмы обработки данных

Кратчайшие пути из одной вершины. Кратчайшие пути в ациклическом ориентированном графе, страница 2

В процессе работы алгоритм поддерживает множество SÍV, состоящее из вершин v, для которых кратчайший путь уже найден (т. е. d[v]=d(S, v)). Алгоритм выбирает вершину UÎV\S с наименьшим d[u],добавляет uк множеству S и производит релаксацию всех ребер, исходящих из u, после чего цикл повторяется.

Вершины, не лежащие в S, хранятся в очереди с приоритетами Q, в которой приоритет определяется минимальным значением d.

Пусть граф задан списком смежных вершин.

Dijkstra(G, w, S)

Initialize_Single_Source(G, S)

1.  S←0

2.  Q←V[G]

3.  while Q¹0

4.       do u←Extract_Min(Q)   O(log V)

5.            S=SÈ{u}

6.            for (для) всех вершин vÎAdj[u]

7.               do Relax (u, v, w)


Пути:

s             u:   u→x→s                         s              v:    v←u←x←s

s             x:    x→s                              s              y:     y←x←s

Оценка времени работы алгоритма Дейкстры: Если очередь с приоритетами реализована в виде обычного массива, то стоимость операции Extract_Min = O(V). Поскольку алгоритм Дейкстры делает |v| таких итераций, то суммарная стоимость удалений оценивается O(V2). Общая стоимость релаксаций оценивается количеством ребер и в конечном счете равна O(E). Т.о. общая стоимость алгоритма Дейкстры O(V2 + E) = O(V2).

Если граф разреженный, то имеет смысл организовать очередь в виде двоичной кучи. Тогда стоимость операции Extract_Min = O(log V). Стоимость построения очереди Q - O(V).

Присваивание d[v] ← d[u] + w(u, v) в функции Relax реализуется при сканировании двоичной кучи и оценивается O(log V). Количество релаксации - E. Т. о. общая стоимость модифицированного алгоритма Дейкстры O((V + E) log V). Поскольку E ³ |V| + 1, то оценка имеет вид: O(ElogV).

Алгоритм Беллмана-Форда.

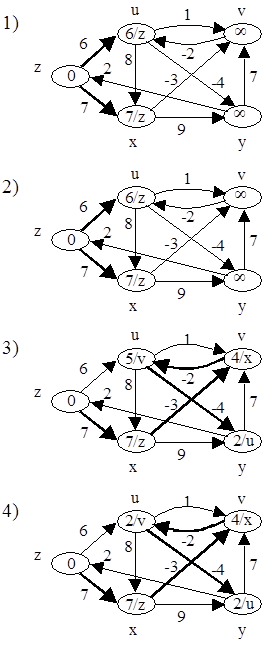
Алгоритм Беллмана-Форда решает задачу о кратчайших путях из одной вершины для случая, когда веса ребер могут быть отрицательными. Алгоритм возвращает значение TRUE если в кратчайших путях нет отрицательного цикла и FALSE, если такой цикл есть. В первом случае алгоритм находит кратчайшие пути и их веса, во втором случае - кратчайших путей - нет.

Подобно алгоритму Дейкстры алгоритм производит релаксацию ребер, пока d[v] не сравняются с d(S, v) для всех vÎV\S;

Bellman_Ford (G, w, S)

1.  Initialize_Single_Source(G, S)

2.  for i ←1 to | V[G] | - 1

3.      do for (для) каждого ребра (u, v)ÎE[G]

4.               do Relax (u, v, w)

5.  for (для) каждого ребра (u, v)ÎE[G]

6.       do if d[v]>d[u] + w(u, v)

7.                then return FALSE

8.  return TRUE.


Пример: Исходная вершина - z.

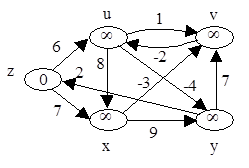После инициализации алгоритм |V| - 1 раз перебирает по все ребра и подвергает каждое из них релаксации.


После этого алгоритм проверяет нет ли цикла отрицательного веса, достижимого из исходной вершины. Признаком этого является наличие на кратчайшем пути ребер (u, v), для которых  d[v] < d[u] + w(u, v). Время работы алгоритма - O(VE). Количество итерации равно |V| - 1,     т. к. на кратчайших путях не может быть более |V| - 1 ребер.

Кратчайшие пути в ациклическом ориентированном графе.

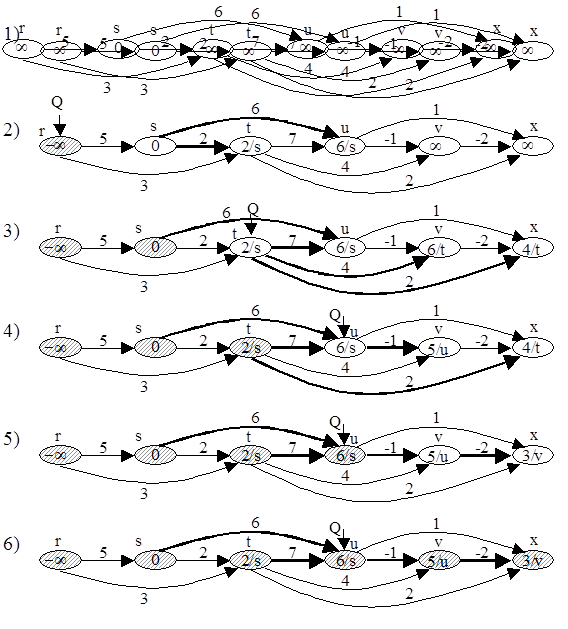
В ациклическом орграфе G = (V, E) кратчайшие пути из одной вершины можно найти за время O(V + E), если  проводить релаксацию ребер в порядке, заданном топологической сортировкой. В ациклическом графе кратчайшие пути всегда определены, поскольку циклов нет.

Алгоритм топологической сортировки располагает вершины орграфа в линейном порядке так, что все ребра идут в одном направлении. После этого вершины просматриваются в этом порядке и для каждой вершины подвергаются релаксации все исходящие ребра.

            Sorted_Sportfest_Pathes (G, w, S)

1.  Q ← Topological_Sort (G)

2.  Initialize_Single_Source(G, S)

3.  while Q ¹ 0

4.     do

5.          u ← Dequene(Q)

6.              for (для) всех вершин vÎAdj[u]

7.                   do Relax (u, v, w)


Допустим, в результате топологической сортировки и его инициализации получен следующий граф:

Оценка времени алгоритма:

Время топологической сортировки (время обхода в глубину) - O(V + E). Время инициализации - O(V). В цикле 3 - 7 каждое ребро обрабатывается 1 раз, т. е. общее время - O(E). Т. о. общее время алгоритма оценивается величиной O(V + E).

Этот алгоритм имеет интересное приложение - нахождение критических путей в смысле так называемой технологии PERT (program avaluation and review technique). В этой технологии каждое ребро ациклического орграфа обозначает к. - я. работу (функцию), а вес ребра - время, необходимое на ее выполнение. Если есть ребра (u, v) и (v, x), то работа, соответствующая ребру (u, v) должна быть выполнена раньше работы соответствующей работе (v, x). Критический путь - самый длинный путь в графе. Его вес равен времени, необходимому на выполнение всех работ, если некоторые работы  выполнять максимально параллельно. Чтобы найти критический путь, можно поменять знак всех весов на противоположный и запустить алгоритм Sorted_Shortest_Pathes.

Скачать файл