12. return D
Общее время работы алгоритма - O(VE log V), что меньше, чем в алгоритме Флойда - Уоршолла (O(V3)).
Паросочетания в двудольном графе.
Двудольным графомназывается граф, в котором все вершины разбиты на два подмножества V1 и V2 так, что каждое ребро графа имеет один конец в V1, а другой в V2.
Задача поиска паросочетания в двудольном графе заключается в следующем: Необходимо найти такое подмножество ребер, в котором нет инцидентных ребер, т. е. ребер имеющих концом одну и ту же вершину.
Задача нахождения максимального паросочетания заключается в поиске максимального подмножества инцидентных ребер.
Полным паросочетанием называется подмножество неинцидентных ребер, соединяющих все вершины графа. Полное паросочетание является максимальным паросочетанием.
Примером задачи поиска максимального паросочетания является следующая задача:
Пусть в графе заданы группа вершин, соответствующих читаемым курсам, и группа вершин, соответствующая преподавателям способным читать те или иные курсы. Преподавтель может читать более одного курса.
 |
Существуют прямые способы простого перебора всех возможных паросочетаний и выбора из них максимального по числу ребер. Но время такого подхода экспоненциально зависит от числа вершин. Метод, который дает эффективное решение используют чередующуюся цепь.
Пусть M - паросочетания в графе G. Относительно паросочетания М вершины графа делятся на два подмножества - парные вершины {Vп} и непарные (свободные) вершины {Vнп}. Паросочетание М можно увеличить, если построить путь Р, соединяющий 2 непарные вершины и включающий в одно или несколько ребер паросочетания. Особенностью этого пути является то, что в нем чередуются ребра, не принадлежащие паросочетанию, и принадлежащему на концах пути находятся ребра ÏМ.
Имея чередующуюся цепь можно увеличит паросочетание М, удалив из него те ребра, которые входят в цепь Р, и добавить вместо них ребра, которые не входили в паросочетание. Эту операцию называют симметрической разностью множеств МDР, в которую входят в те элементы двух множеств, которые принадлежат или М или Р.
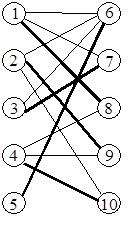
Пример: М = {1 - 6, 3 - 7, 4 - 8}
Vп = {1, 3, 4, 6, 7, 8}
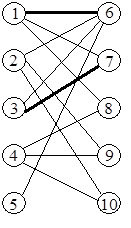 |
Симметрическая разность, МDР = {2 - 6, 1 - 8, 4 - 9, 3 - 7}. Эта разность является новым увеличенным паросочетанием.
Паросочетание будет максимальным, тогда когда не существует чередующейся цепи относительно М.
Алгоритм нахождения максимального паросочетания следующий:
Max_Pair(G)
1. Mß0
2. repeat
3. PßPath_Link(G, M)
4. MßMDP
5. until P ¹ 0
Алгоритм Path_Link формирует чередующуюся цепь в виде множества ребер.
Алгоритм делит множество вершин на парные и непарные относительно паросочетания {Vp} и {Vnp}.
Построение чередующейся цепи напоминает алгоритм обхода в ширину и выполняется по шагам i = 0, 1, 2, ... . На нулевом шаге вершины графа делятся на подмножества {Vp} и {Vnp} и выбирается произвольно непарная вершина. Далее на 1 - м шаге выбирается ребро, не принадлежащее паросочетанию М и ведущее к парной вершине из множества {Vп}.
На 2 - м шаге и последующих четных шагах выбирается инцидентная для последней вершины пути ребро, принадлежащее М.
На 3 - м и последующих шагах выбирается инцидентное последней вершине пути ребро, не принадлежащее М. При этом, в первую очередь выбирается ребро, ведущее к свободной вершине. Если таковой нет, то выбирается ребро, не принадлежащее М и ведущие к парной вершине.
Вершины, включенные в путь Р удаляются из множества {Vнп}.
Процесс построения заканчивается, когда будет включено ребро, ведущее к непарной вершине.
Path_Link(G, M)
1. Vpß{vÎM}
2. VnpßV[G]\Vp
3. Pß 0
4. Выбор v0ÎVnp
5. Выбор (v0, v1) D v1 ÎVp
6. PßPÈ( v0, v1)
7. K = 0
8. Repeat
9. KßK + 1
10. Vnp = Vnp\vk
11. Выбор (vk, vk+1) ÎM
12. PßPÈ( vk, vk+1)
13. KßK + 1
14. if $ ( vk, vk+1) Ï M and vk+1ÏVp
15. then PßPÈ{( vk, vk+1) Ï M}
16. else p ßPÈ{( vk, vk+1) Ï M }
17. until vk+1 Î Vp
18. return P
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.