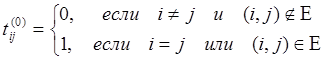 |
Для k ³1: t(k)ij = t(k-1)ij Ú ( t(k-1)ik Ù t(k-1)kj)
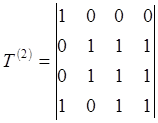
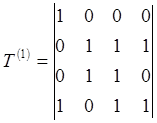
 |
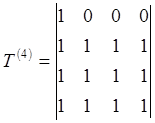
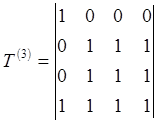 |
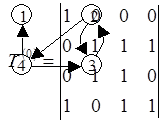
Алгоритм транзитивного замыкания последовательно вычисляет матрицы T(k) =(t(k)ij) для k = 1,2,...,n.
Transitive_Closure(G)
1. n←V[G]|
2. for i←1 to n
3. do for i←1 to n
4. do if i=j или (i, j)ÎE[G]
5. then t(0)ij ←1
6. else =t(0)ij←0
7. for k←1 to n
8. do for i←1 to n
9. do for j←1 to n
10. do t(k)ij ← t(k-1)ij Ú ( t(k-1)ik Ù t(k-1)kj)
11. return T(n)
Алгоритм Джонсона нахождения всех пар кратчайших путей.
Этот алгоритм работает эффективнее, чем алгоритм Флойда - Уоршолла для разреженных графов. Его время O(V2 log V + VE). Алгоритм либо формирует матрицу кратчайших путей, либо сообщает, что в графе имеется цикл отрицательного веса. Работа алгоритма основана на использовании алгоритмов Беллмана - Форда и Дейкстры.
Особенностью алгоритма является изменения весов ребер графа, т. о. чтобы они были неотрицательны, и можно было бы применить алгоритм Дейкстры к каждой вершине.
При изменении весов ребер должны быть соблюдены следующие условия:
1) Кратчайшие пути в графе не изменяются, т. е. для любой пары вершин u, v ÏV кратчайший путь с точки зрения исходной весовой функции w совпадает с кратчайшим путем с точки зрения новой весовой функции ~w.
2) Все новые веса ~w(u, v) неотрицательны.
Необходимо подобрать способ изменения весов ребер с соблюдением этих условий.
Пусть дан граф G=(V, E) с весовой функцией w: EàR. Введем весовую функцию для вершин графа h: VàR.
Рассмотрим новую весовую функцию ~w: EàR, такую, что ~w(u, v)= w(u, v) + h(u) - h(v). Тогда любой кратчайший путь p = (v0, v1,..., vk) относительно w будет совпадать с кратчайшим путем относительно ~w.
![]() Вес любого
пути v0 vk относительно
~w(p)
равен:
Вес любого
пути v0 vk относительно
~w(p)
равен:
~w(p)= w(p) + h(v0) - h(vk).
Т. е. для всех путей с фиксированным началом и концом разница между старым и новым весом постоянна и поэтому кратчайшие пути для новой и старой весовой функции совпадают.
~w(p)= w(v0, v1,) + h(v0)
- h(v1) + w(v1, v2,) + h(v1)
- h(v2) +... +w(vk-1, vk,) + h(vk-1)
- h(vk) =
= w(v0, vk,) + h(v0) - h(vk)
Второе следствие при таком преобразовании:
Если граф G содержит отрицательный цикл относительно весовой функции w, то он содержит этот же отрицательный цикл относительно функции ~w. Это следствие исходит из того, что вес цикла равен:
~w(p)= w(p) + h(v0) - h(v0).
Чтобы перейти к новой весовой функции с неотрицательными весами нужно подобрать весовую функцию h: VàR.
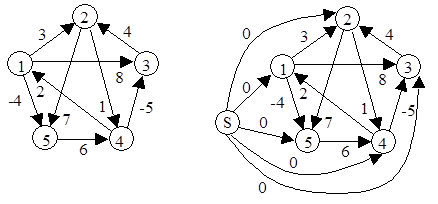 |
Введение этой вершины не изменит путей в новом графе, поскольку вершина S, не может быть вставлена в качестве промежуточной в пути, т. к. не имеет входящих ребер. Она может быть только начальной вершиной пути. Новый граф содержит цикл отрицательного веса, если таковой содержится в исходном графе.
Пусть граф G`, как и граф G не содержит цикла отрицательного веса. Пусть вес каждой вершины равен весу кратчайшего пути до этой вершины S, т. е. h(v) = d(S, v) для " vÎV`.
Для вершин, лежащих на кратчайшем пути выполняется свойство: h(v)£h(u)+w(u, v). Поэтому w(u, v) + h(u) - h(v) ³ 0, т. е. новая весовая функция ~w(u, v) = w(u, v) + h(u) - h(v) неотрицательна.
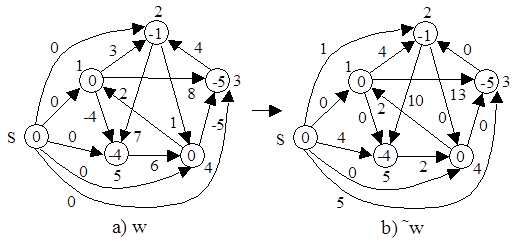
Далее для прокладки кратчайших путей используется алгоритм Дейкстры.
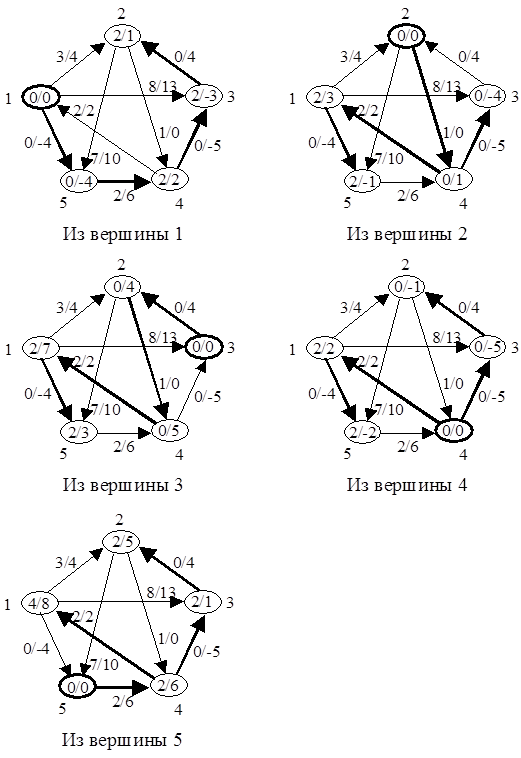 |
Орграф для алгоритма Джонсона лучше представит в виде списков смежности. Это представление больше подходит для разреженных графов.
Алгоритм возвращает матрицу D = |dij| размера |V| * |V|, где dij = d(i, j), или возвращает сообщение о том, что граф имеет отрицательный цикл. Вершины нумеруются от 1 до |V|.
Johnson(G)
1. Создать граф G`, для которого V[G`] = V[G]È{S} и E[G`] = E[G]È{S, v}: vÎV[G]
2. if Bellman_Ford(G`, w, S) = FALSE
3. then печать "имеется цикл отрицательного веса"
4. else for (для) каждой вершины vÎV[G`]
5. do h(v)ßd[v] d[v] вычислено в Bellman_Ford
6. for (для) каждого ребра (u, v)ÎE[G`]
7.
![]()
![]()
![]() do
~w(u, v)ßw(u,
v) + h(u) - h(v)
do
~w(u, v)ßw(u,
v) + h(u) - h(v)
8. for (для) каждой вершины uÎV[G]
9. do Dijkstra(G, ~w, u) вычисление |~d|
10. for (для) каждой вершины vÎV[G]
11. do d ß ~d[v] + h[v] - h[u] вычисление |d|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.