Разработка абстрактного типа данных «Простой граф», страница 6

V	E	T	теория
500	50	1	25000
	100	1	50000
	1000	1410	500000
	5000	20110	2500000
	10000	52780	5000000
	50000	422949	25000000
V	E	T	теория
10000	50	1	500000
	100	1	1000000
	1000	1	10000000
	5000	3	50000000
	10000	106	100000000
	50000	177172	500000000

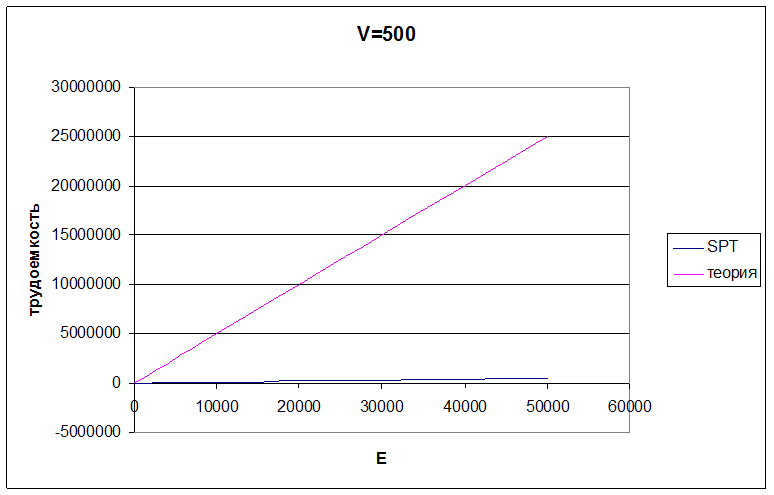
Рис. 3.4 Трудоемкость алгоритма при количестве вершин 500

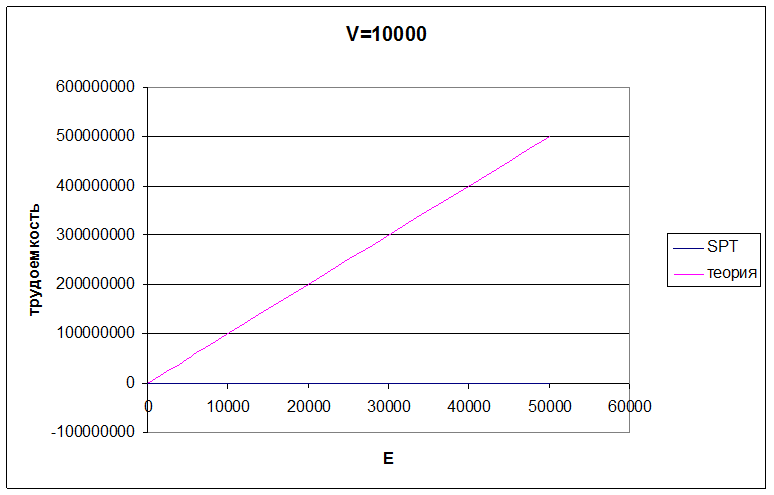
Рис. 3.5 Трудоемкость алгоритма при количестве вершин 10000

Выводы:

Экспериментальная трудоемкость алгоритма Беллмана-Форда не превышает теоретическую.

В ненасыщенном графе практическая трудоемкость значительно ниже теоретической.

Описание интерфейса визуализатора.

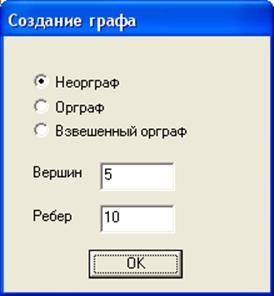
Рис. 4.1 Создание графа

При запуске предлагается создать граф с определенными параметрами

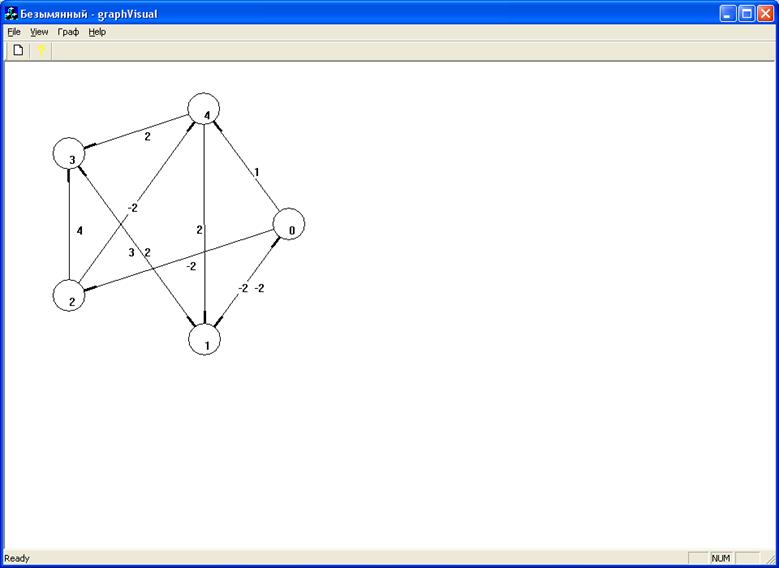
Рис. 4.2 Рабочая область (на примере взвешенного орграфа)

Граф представляет собой набор окружностей и линий. Направление стрелки показывает утолщение на конце ребра. Показаны также веса всех ребер. Для того, чтобы можно было располагать вершины графа в удобном виде, в программе реализована возможность перетаскивания вершин графа по рабочей области документа.

Рис. 4.3 Меню

В меню можно выбрать работу с графом, преобразование внутреннего представления графа и задачи по варианту.

Рис. 4.4 Базовые операции над графом

Можно вставлять, удалять ребра; изменять веса ребер. Визуализация работы итератора (ребро к смежной вершине подкрашивается). Предусмотрена очистка цветовой окраски графа (Сброс).

Заключение

В данной работе рассмотрена реализация ориентированных/неориентированных взвешенных/невзвешенных графов в виде списков смежности и в виде матрицы смежности. Реализованы три алгоритма на графах. По ним можно сделать следующие выводы:

Алгоритм DFS универсален, на нем основано много важных алгоритмов на графах.

Алгоритм Беллмана-Форда очень хорошо себя показывает на ненасыщенных графах, а его максимальная теоретическая трудоемкость O(VE), что позволяет использовать его в реальных приложениях, это выявлено из эксперимента и видно на графике на Рис.3.4

Список литературы

1. Фундаментальные алгоритмы на C++. Алгоритмы на графах: Пер. с англ./Роберт Седжвик. СПб: ООО «ДиаСофтЮП», 2002. – 496 с.

2. Лекции по курсу «Структуры и алгоритмы обработки данных», преп. Романенко Т.А.

Приложение

ATD.h

#ifndef _GraphATD

#define _GraphATD

 

template<class T1>

class GraphATD

{

public:

      virtual int V()=0;//    - опрос числа вершин в графе,

      virtual int E()=0;//    - опрос числа ребер в графе,

      virtual bool Directed()=0;//  опрос типа графа (ориентированный / неориентированный)

      virtual bool Weighed()=0;//   опрос типа графа (взвешенный)

      virtual int Dense()=0;//           опрос формы представления графа (L- граф / M- граф),

      virtual bool Insert(int,int)=0;//  вставка ребра, соединяющего вершины v1, v2,

      virtual bool Delete(int,int)=0;//  удаление ребра, соединяющего вершины v1, v2,

      virtual bool Edge(int,int)=0;//    опрос наличия ребра, соединяющего вершины v1, v2,

      virtual bool SetEdge(int,int,T1)=0;//          задание параметров ребра,

      virtual GraphATD<T1>* ToListGraph()=0;

      virtual GraphATD<T1>* ToMatrixGraph()=0;

      virtual T1* GetEdge(int,int)=0;

      virtual ~GraphATD(){};

};

 

#endif

 

#ifndef _IteratorATD

#define _IteratorATD

 

template<class T1>

class IteratorATD

{

public:

      virtual bool beg(int&)=0;//установка итератора на первую смежную вершину,

      virtual bool off()=0;//oпрос окончания просмотра смежных вершин,