Разработка абстрактного типа данных «Простой граф», страница 5

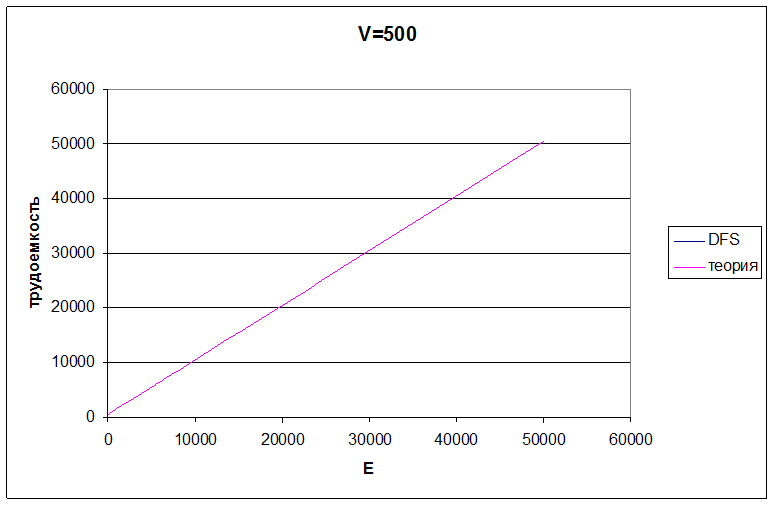
Рис.3.1 Трудоемкость алгоритма обхода в глубину при количестве вершин 500

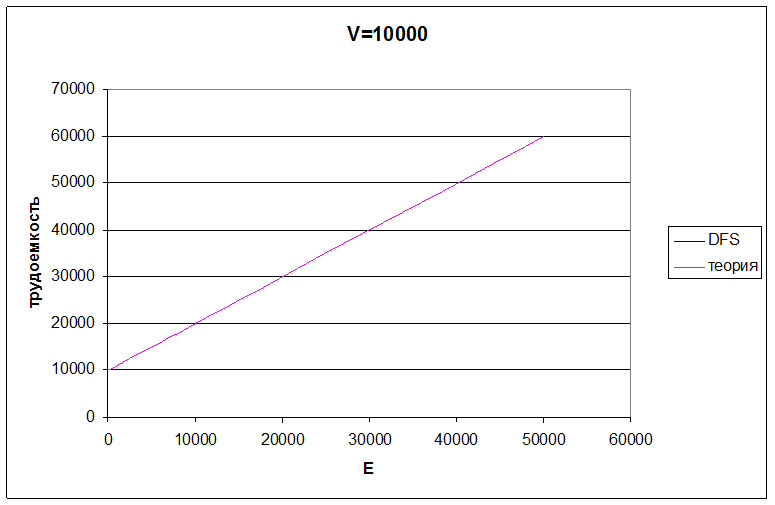
Рис.3.2 Трудоемкость алгоритма обхода в глубину при количестве вершин 10000

Выводы:

Проанализировав полученные результаты, можно сделать вывод о том, что трудоёмкость алгоритма не зависит от структуры графа. Это можно объяснить тем, что алгоритм DFS просматривает один раз каждое ребро и каждую вершину, следовательно, с увеличением  количества рёбер линейно увеличивается трудоёмкость работы алгоритма. По этой же причине нет отличий от теоретической трудоёмкости.

Теоретическая трудоёмкость: O(V+E);

Задача 2

12) топологической сортировки ациклического орграфа DAG на основе очереди истоков

Описание алгоритма:

Поддерживатся очередь истоков и использует таблицу, которая отслеживает полустепени захода каждой вершины графа DAG, индуцированного вершинами, которые еще не удалены из очереди.

Когда мы удаляем исток из очереди, мы уменьшаем значения полустепеней захода, соответствующих каждой вершине в его списке смежных вершин (и помещаем в очередь каждую вершину, соответствующую элементу таблицы, принимающему значение 0). Вершины покидают очередь в порядке топологической сортировки.

 В этой задаче тестировалась трудоемкость топологической сортировки.

Таблица 2

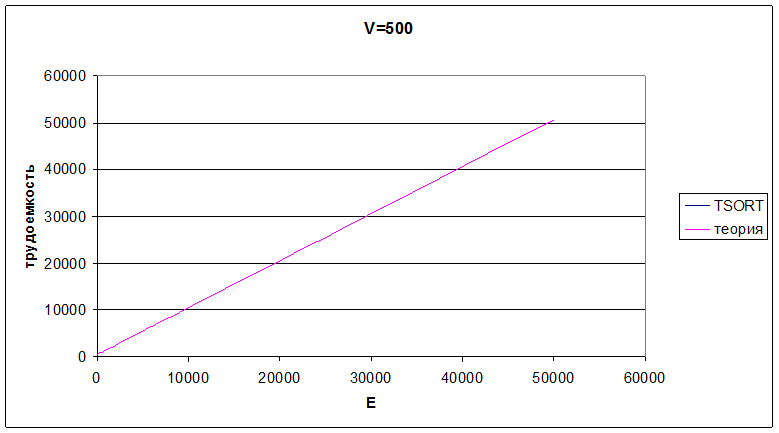
Рис. 3.3 Трудоемкость алгоритма при количестве вершин 500

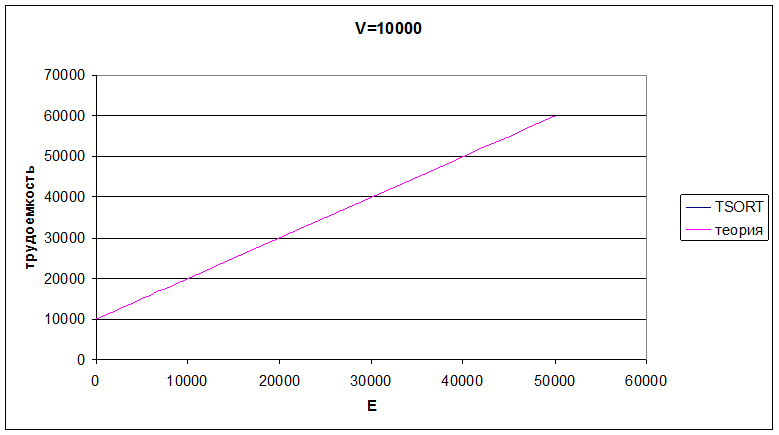
Рис. 3.4 Трудоемкость алгоритма при количестве вершин 10000

Выводы:

По результатам эксперимента можно сделать вывод о том, что трудоёмкость линейно зависит от V и E.

Теоретическая трудоёмкость: O(V+E); Получено полное совпадение с теорией.

Задача 3

4)  определение списка вершин, которые лежат в пределах заданного расстояния d от заданной вершины взвешенного орграфа с отрицательной весовой функции на основе алгоритма Беллмана-Форда

Краткое описание алгоритма:

Сперва производится поиск отрицательных циклов и, если их нет, выполняется алгоритм Беллмана-Форда.

Эта реализация алгоритма поддерживает очередь FIFO всех вершин, для которых ослабление вдоль исходящего ребра могло бы оказаться эффективным. Берется вершина из очереди и производится ослабление вдоль всех ее ребер. Если любое из них приводит к более короткому пути в некоторую вершину, мы помещаем ее в очередь. Теоретическая трудоемкость для худшего случая O(VE).

Проводилось по 100 запусков, брался средний результат.

Таблица 3