Statistica были рассчитаны числовые характеристики показателя (табл.2) и построена гистограмма (рис.2).
Таблица 2. Числовые характеристики времени нахождения заявки в системе
|
Minimum |
Maximum |
Range |
Variance |
Std.Dev. |
|
|
tc |
0,1310 |
85,7940 |
85,6630 |
256,7851 |
16,0245 |
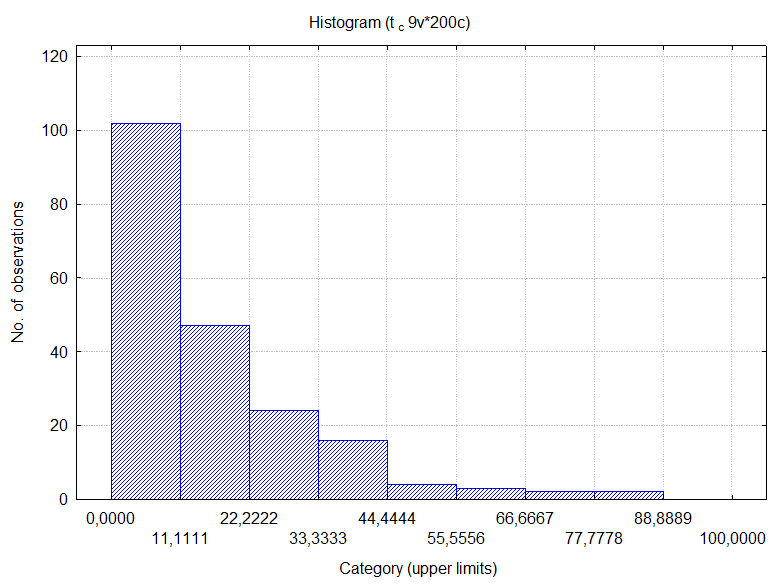
Рис.2. Гистограмма распределения времени нахождения заявки в системе
H0: показатель «время нахождения заявки в системе» распределен по экспоненциальному закону.
H1: показатель «время нахождения заявки в системе» не распределен по экспоненциальному закону.
Пусть уровень значимости α = 0,05.
Количество
категорий: ![]()
Проверим гипотезу о распределении времени пребывания заявки в системе по закону Гамма на основе критерия хи-квадрат средствами Statistica.
Таблица 3.
|
Observed |
Cumulative Observed |
Percent Observed |
Cumul. % Observed |
Expected Frequency |
Cumulative Expected |
Percent Expected |
Cumul. % Expected |
Observed- Expected |
|
|
<= 11,111 |
102 |
102 |
51,00000 |
51,0000 |
100,1368 |
100,1368 |
25,03421 |
50,0684 |
1,86318 |
|
22,222 |
47 |
149 |
23,50000 |
74,5000 |
49,9999 |
150,1367 |
12,49998 |
75,0684 |
-2,99991 |
|
33,333 |
24 |
173 |
12,00000 |
86,5000 |
24,9657 |
175,1025 |
6,24144 |
87,5512 |
-0,96575 |
|
44,444 |
16 |
189 |
8,00000 |
94,5000 |
12,4658 |
187,5683 |
3,11645 |
93,7841 |
3,53421 |
|
55,555 |
4 |
193 |
2,00000 |
96,5000 |
6,2244 |
193,7926 |
1,55609 |
96,8963 |
-2,22437 |
|
66,666 |
3 |
196 |
1,50000 |
98,0000 |
3,1079 |
196,9006 |
0,77698 |
98,4503 |
-0,10793 |
|
77,777 |
2 |
198 |
1,00000 |
99,0000 |
1,5518 |
198,4524 |
0,38796 |
99,2262 |
0,44816 |
|
88,888 |
2 |
200 |
1,00000 |
100,0000 |
0,7749 |
199,2273 |
0,19371 |
99,6136 |
1,22514 |
|
< Infinity |
0 |
200 |
0,00000 |
100,0000 |
0,7727 |
200,0000 |
0,19318 |
100,0000 |
-0,77274 |
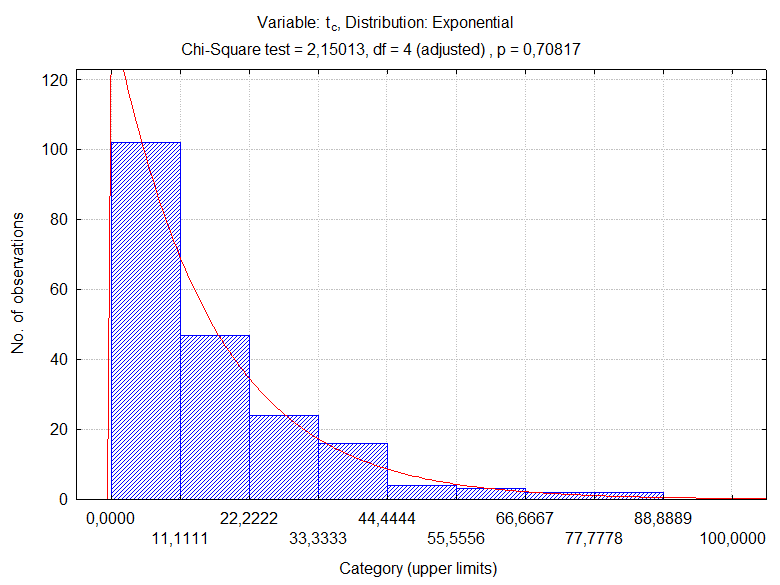 Рис. 3. Гистограмма распределения
времени нахождения заявки в системе
Рис. 3. Гистограмма распределения
времени нахождения заявки в системе
c наложением закона Гамма
Поскольку p-значение не меньше α (0,70817>0,05), гипотеза H0 призаданном уровне значимости не отвергается.
Таблица 4.
|
Генераторы обработки |
Среднее время пребывания требования в системе |
Среднее время обработки одной заявки |
|
1,1,1 |
15,903 |
15,903 |
|
1,3,5 |
15,372 |
15,372 |
|
1,2,3 |
15,903 |
15,903 |
|
1,4,7 |
15,903 |
15,903 |
|
2,4,6 |
15,790 |
15,790 |
|
2,3,4 |
15,790 |
15,790 |
|
5,5,5 |
15,790 |
15,790 |
|
2,2,2 |
15,790 |
15,790 |
|
7,7,7 |
15,790 |
15,790 |
|
1,2,7 |
15,903 |
15,903 |
Среднее время пребывания требования в системе по результатам 10 экспериментов:
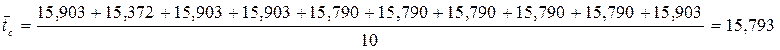 Среднее время обработки одной заявки
каналами результатам 10 экспериментов:
Среднее время обработки одной заявки
каналами результатам 10 экспериментов:
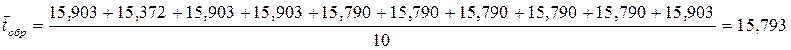
Среднее время ожидания в очереди по результатам 10 экспериментов:
![]()
3.2. Имитация СМО с учетом дополнительных условий
Задание: приоритеты каналов соответственно 1, 2, … n. Вероятность безошибочного обслуживания заявки 0.9, таким
образом интенсивность обслуживания ![]() =0.9
=0.9![]()
Вероятность простоя системы: ![]()
Вероятность загрузки системы: ![]()
Вероятность загрузки 1 канала: ![]()
Вероятность загрузки 2 канала: ![]()
Вероятность загрузки 3каналов (без очереди): ![]()
Вероятность загрузки 3каналов (с 1 заявкой в очереди): ![]()
Вероятность загрузки 3каналов (с 2 заявками в очереди): ![]()
Вероятность загрузки канала I:
![]()
Вероятность загрузки канала II:
![]()
Вероятность загрузки канала III:
![]()
Вероятность отказа в обслуживании: ![]()
Среднее число требований в
очереди: ![]()
Среднее число заявок в
системе: ![]()
Среднее число занятых каналов:
![]()
Среднее время пребывания
требования в системе: ![]()
Среднее время обработки одной заявки каналами: ![]()
Среднее время ожидания в
очереди: ![]()
Поскольку интенсивность обслуживания уменьшилась увеличились вероятности загрузки как каналов, так и всей системы соответственно. Увеличились также и среднее число заявок в системе, среднее время пребывания требования в системе, среднее время обработки одной заявки каналами. Очередь по-прежнему не используется.
Таблица 5. Ошибки определения параметров СМО
|
Параметр |
Аналитический метод |
Метод ИМ |
Ошибка оценки ε, % |
|
Pзагр |
0,289 |
0,3 |
3,8 |
|
P0 |
0,711 |
0,7 |
1,5 |
|
P1 |
0,2706 |
0,274 |
1,25 |
|
P2 |
0,0179 |
0,0161 |
10 |
|
P3 (без очер) |
0,0004 |
0,0004 |
0 |
|
n0 |
7,2*10-8 |
0 |
абс. 7,2*10-8 |
|
tож |
3,6*10-6 |
0 |
абс. 3,6*10-6 |
|
Nз |
0,3076 |
0,317 |
3 |
|
J |
0,3076 |
0,317 |
3 |
|
tc |
15,384 |
15,903 |
3,4 |
|
tобр |
15,384 |
15,903 |
3,4 |
Выводы:
Анализируя таблицу 5, можно сделать вывод о том, что результаты имитационного моделирования отличаются от значений, рассчитанных аналитически, статистически незначимо. Таким образом в данном случае имитационный метод показывает свою высокую эффективность. Расхождения с аналитическими расчетами можно уменьшить еще больше, изменив последовательность случайно генерируемых чисел.
Так как представленная СМО весьма специфична и имеет свои особенности, о которых ниже, то в районе малых значений есть расхождения (напр, n0 и tож).
Представленная система, хотя и выглядит «быстрой» и не использует предоставленную ей очередь, является очень неэффективной: вероятности загрузки 2 и 3 каналов низки, а вероятность простоя высока. Если увеличить интенсивность входного потока, то картина будет меняться в лучшую сторону. Имитационным методом не были достигнуты состояния полной загрузки (т.е. попадания заявок в очередь) СМО из-за малого количества заявок (200). Поэтому для данной СМО можно предложить избавиться от очереди, если это возможно.
Пример СМО:
Мощный сервер, имеющий три процессора для обработки заданий, а также очередь заданий. На сервер поступают нетребовательные задания через длинные промежутки времени. Поэтому высока вероятность простоя, а возникновение очереди маловероятно. Введение дополнительных условий – небольшое падение производительности (пересчет задач с ошибкой) также вписывается в данную СМО.
В итоге для СМО можно сказать следующее:
По результатам исследований имитационное моделирование намного эффективнее аналитического расчета, позволяет быстро и просто вычислить вероятности состояний, а погрешности статистически незначимы. Аналитический расчет же более сложен, требует больших затрат времени на расчеты, построения графа состояний и решения дифуравнений.
Литература
Приложение. Исходный текст программы имитации СМО с одинаковыми интенсивностями обслуживания каналов
TAB TABLE M1,8,8,11 ;сбор информации о МО и СКО
GENERATE (EXPONENTIAL(1,0,16.66)+EXPONENTIAL(3,0,16.66)+EXPONENTIAL(5,0,16.66)),,,200
;распределение входного потока заявок
TEST L Q$SIS,5,OUT
QUEUE SIS
TRANSFER All,K1,K3,5
K1 SEIZE 1
ADVANCE (EXPONENTIAL(1,0,15.38)) ;обработка заявок 1 каналом
DEPART SIS
RELEASE 1
TRANSFER,OUT
K2 SEIZE 2
ADVANCE (EXPONENTIAL(1,0,15.38)) ;обработка заявок 2 каналом
DEPART SIS
RELEASE 2
TRANSFER,OUT
K3 SEIZE 3
ADVANCE (EXPONENTIAL(1,0,15.38)) ;обработка заявок 3 каналом
DEPART SIS
RELEASE 3
OUT SAVEVALUE 1+,1
SAVEVALUE X1,M1
SAVEVALUE TIME,C1 ;общее время моделирования
TABULATE TAB
TERMINATE 1
START 200 ;общее количество заявок
GENERATE 0,,,1
MET ADVANCE 1
TEST G Q$SIS,0,MET
SAVEVALUE ZAGR+,1 ;общее время загрузки системы
TEST E Q$SIS,1,MET1
SAVEVALUE ZAGR1+,1 ;время пребывания в системе 1 заявки
TRANSFER ,MET
MET1 TEST E Q$SIS,2,MET2
SAVEVALUE ZAGR2+,1 ;время пребывания в системе 2 заявок
TRANSFER ,MET
MET2 TEST E Q$SIS,3,MET3
SAVEVALUE ZAGR3+,1 ;время пребывания в системе 3 заявок
TRANSFER ,MET
MET3 TEST E Q$SIS,4,MET4
SAVEVALUE ZAGR4+,1 ;время пребывания в системе 4 заявок
TRANSFER ,MET
MET4 SAVEVALUE ZAGR5+,1 ;время пребывания в системе 5 заявок
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.