Термическое расширение материалов. Тепловые колебания и другие факторы, определяющие коэффициент термического расширения материала. Методы дилатометрического анализа

8. ТЕРМИЧЕСКОЕ РАСШИРЕНИЕ  МАТЕРИАЛОВ

8.1.  Основные понятия

При нагревании все материалы независимо от их агрегатного состояния расширяются. В твердых телах такое расширение связывают с увеличением межатомного расстояния в решетке. Экспериментальная зависимость длины образца  от температуры носит сложный нелинейный характер, описываемый степенным полиномом

                                                            (8.1)

где  L – длина образца при температуре нагрева Т; L₀ -  исходная длина при исходной температуре Т₀, α₁, α₂, α₃, … - постоянные величины; t = T – T₀.

 В практических расчетах обычно ограничиваются линейным членом, тогда выражение (8.1) принимает вид

                                                                          (8.2)

Истинное значение коэффициента линейного расширения при нагревании можно определить

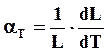                                                                                (8.3)

где L – длина образца.

Объемный коэффициент линейного расширения рассчитывается по формуле

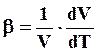                                                                                (8.4)

где   V – объем образца.

Изменение размеров кристаллов при нагревании от температуры Т₁ до Т₂ описывается экспоненциальной формулой

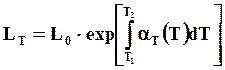                                                                 (8.5)

В предположении α_Т – const формула (8.5) упрощается

                                                                              (8.6)

Объемный коэффициент теплового расширения для изотропного материала  составляет

                                                                                               (8.7)

8.2.  Тепловые колебания и другие факторы, определяющие

коэффициент термического расширения материала

Изменение размеров твердых и жидких тел при нагревании вызвано увеличением расстояния между соседними атомами и связано с асимметричным изменением кривой потенциальной энергии относительно вертикальной линии, проходящей через положения минимума и центра равновесного состояния атомов при нулевой температуре. Асимметричность изменения потенциальной энергии обусловлена различием в изменении сил притяжения и отталкивания при смещении атомов из положения равновесия. При сближении атомов энергия сил отталкивания возрастает быстрее, чем энергия сил притяжения при соответствующем удалении атомов. Поэтому при нагревании, с увеличением амплитуды тепловых колебаний    атомов в кристалле,  расстояние между атомами при сближении уменьшается значительно медленнее, чем оно возрастает при их удалении. Рассмотрим этот процесс более подробно.

На рис. 8.1 схематично показано изменение потенциальной энергии при колебании одного атома относительно другого.

Рис. 8.1.  Изменение потенциальной энергии атомов при тепловом колебании

Прямые линии, проведенныепараллельно абсциссе, характеризуют полную энергию взаимодействующих атомов. Когда атомы находятся по отношению к друг к другу в положении равновесия  на расстоянии r₀, то кинетическая энергия пары будет максимальна, а потенциальная минимальна.  Представим, что один из атомов в паре закреплен, а другой может совершать тепловые колебания относительно него. Тогда при отклонении подвижного атома  влево от положения равновесия кинетическая энергия системы  будет расходоваться на преодоление сил отталкивания подвижного атома относительно неподвижного и переходить в потенциальную энергию взаимодействующих частиц. Отклонение влево будет происходить до тех пор, пока вся кинетическая энергия Е_к не перейдет в потенциальную. При этом потенциальная энергия увеличится на ΔU = E_к и станет равной  U₀ – ΔU, а подвижный атом сместится предельно влево на расстояние Δr₁.

При движении подвижного атома вправо от положения равновесия кинетическая энергия расходуется на преодоление сил притяжения подвижного к неподвижному атому и также переходит в потенциальную. В точке В, отстоящей от положения равновесия на расстоянии Δr₂, вся кинетическая энергия также перейдет в потенциальную, вследствие чего она увеличится на ΔU  и станет равной U₀ – ΔU. Если бы подвижный атом совершал чисто гармонические колебания, то возвращающая в положение