














9. УПРУГИЕ СВОЙСТВА МАТЕРИАЛА
9.1. Основные понятии
Под упругостью понимают способность материала восстанавливать первоначальную форму и размеры после снятия внешних механических нагрузок. Упругость, также как и другие физические свойства, может быть использована для исследования металлов и сплавов при решении задач материаловедения.
Основными количественными характеристиками упругости являются модуль нормальной упругости (Е), модуль сдвига (G) и модуль объемной упругости или модуль всестороннего сжатия (D), вычисляемые как первая производная изменения степени линейной, угловой и объемной деформации от приложенной внешней нагрузки в области проявления закона Гука. Все три модуля упругости связаны между собой соотношениями
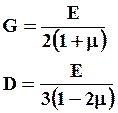 (9.1)
(9.1)
где μ – коэффициент Пуассона.
Коэффициент Пуассона характеризует изменение объема тела при упругой деформации. При одноосном растяжении образца квадратного сечения увеличение объема вследствие его удлинения частично компенсируется поперечным сужением. Аналогичные процессы, но с противоположным знаком происходят при одноосном сжатии. Коэффициент Пуассона в этом случае определяется
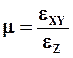 (9.2)
(9.2)
где εZ, εXY – относительное изменение продольных и поперечных размеров образца
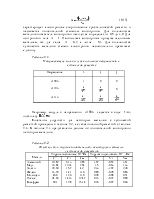
Для большинства металлов и сплавов коэффициент Пуассона находится в пределах 0,25…0,35; наименьшее значение найдено для Be (μ = 0.039), а наибольшее у Pb (μ = 0,44), Tl и In (μ = 0,46).
Для большинства металлов и сплавов выполняется соотношение
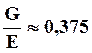 …0,382
(9.3)
…0,382
(9.3)
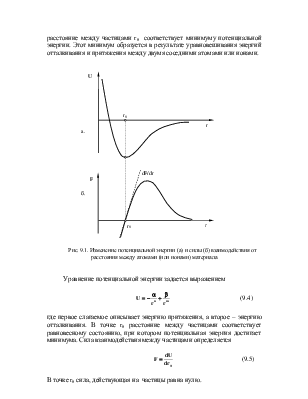
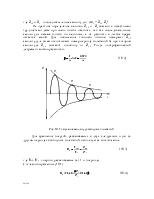
Упругие свойства определяются силами связей между соседними элементарными частицами в материале (атомами или ионами). Рассмотрим, как изменяется потенциальная энергия пары соседних частиц U в зависимости от разделяющего их расстояния r (рис.9.1). Равновесное расстояние между частицами r0 соответствует минимуму потенциальной энергии. Этот минимум образуется в результате уравновешивания энергий отталкивания и притяжения между двумя соседними атомами или ионами.

Рис. 9.1. Изменение потенциальной энергии (а) и силы (б) взаимодействия от расстояния между атомами (или ионами) материала
Уравнение потенциальной энергии задается выражением
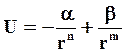 (9.4)
(9.4)
где первое слагаемое описывает энергию притяжения, а второе – энергию отталкивания. В точке r0 расстояние между частицами соответствует равновесному состоянию, при котором потенциальная энергия достигает минимума. Сила взаимодействия между частицами определяется
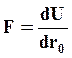 (9.5)
(9.5)
В точке r0 сила, действующая на частицы равна нулю.
Первая производная от силы по расстоянию, разделяющему частицы, описывает жесткость или обоюдное сопротивление частиц разделению друг от друга
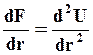 (9.6)
(9.6)
Выражение (9.6) представляет аналог модуля Юнга, который в упругой области пропорционален второму слагаемому, т.е.
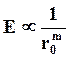 (9.7)
(9.7)
Следовательно, модуль упругости определяется равновесным расстоянием между частицами. С повышением температуры значение r0 возрастает, приводя к уменьшению модуля упругости.
Поскольку модуль упругости Е зависит от прочности сил межатомной связи, которые изменяются только сообразно типу взаимодействия частиц в том или ином конкретном материале, этот параметр практически не чувствителен к изменениям микроструктуры. Этот факт находит экспериментальное подтверждение. Так, если термообработкой и легированием можно сильно изменить структуру и повысить прочность стали на один порядок и более, то модуль упругости при этом возрастает всего на 5…10%.
9.2. Обобщенный закон Гука
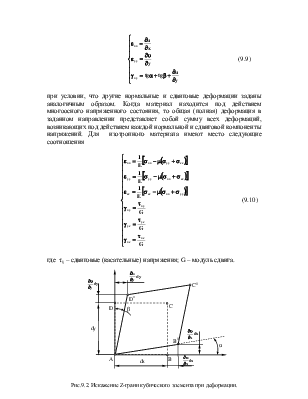
Закон Гука можно обобщить для случая многоосного нагружения, как изотропного, так и анизотропного материала. Напряжение, действующее в одном направлении (допустим вдоль оси Y) вызовет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.