Разработка методов, аппаратных и программных средств для регистрации, обработки и анализа сигналов акустической эмиссии, страница 8

Для оценки вклада детализирующих коэффициентов вейвлет–преобразования было определено их среднеквадратическое отклонение (СКО). СКО рассчитано по стандартной формуле:

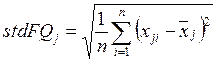
гдеstdFQ_j – среднеквадратическое отклонение j-го коэффициента вейвлет-разложения сигнала АЭ,

n – число отсчетов дискретизации сигнала АЭ,

x_ji – численное значение i-го отсчета j-го вейвлет-коэффициента,

 - среднее значение ряда из n отсчетов j-го вейвлет-коэффициента.

Далее проведен анализ зависимости их значений от величины удаления источника АЭ от приемника. На рис. 3.2.4 приведены значения среднеквадратического отклонения, характеризующие флуктуации детализирующих вейвлет–коэффициентов каждого масштаба в зависимости от расстояния датчик – излучатель. Вариант практической реализации подобного метода обработки данных для кардиосигнала и временных рядов цен акций, описан в работах [260, 261].

Анализ данных показал, что в явном виде можно выделить несколько характерных групп значений среднеквадратического отклонения: кривая, соответствующая вейвлет коэффициенту FQ4 (260,42 кГц) с максимальным значением; кривые, соответствующие коэффициентам FQ3 (520,83 кГц) и FQ5 (130,21 кГц), а также кривые, определенные для коэффициентов FQ2 (1041,67 кГц) и FQ6 (65,10 кГц). СКО каждого соответствующего вейвлет–коэффициента практически не изменяется с увеличением расстояния. Таким образом, СКО вейвлет–коэффициентов может быть использовано в качестве частотного критерия, характеризующего источник сигнала АЭ и не зависящего от его местоположения.

Количественная оценка спектральных составляющих сигналов АЭ по m вейвлет-коэффициентам представляется не совсем удобной и не достаточно наглядной. В связи с этим для повышения информативности на основании данных по рассчитанным коэффициентам вейвлет разложения был разработан количественный параметр, названный частотным коэффициентом K_f. Физический смысл частотного коэффициента K_f можно определить как вклад частотных компонент спектра вейвлет-разложения в сигнал АЭ в целом. Частотный коэффициент K_f был рассчитан по формулам (1, 2):

,

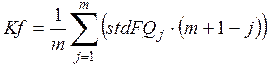где stdFQ_j– среднеквадратическое отклонение j-го коэффициента вейвлет-разложения сигнала АЭ, n – число отсчетов дискретизации сигнала АЭ, m – число коэффициентов вейвлет-разложения, x_ji – численное значение i-го отсчета j-го вейвлет-коэффициента,  - среднее значение ряда из n отсчетов j-го вейвлет-коэффициента.

В отличие от такого параметра как медианная частота, он определяется по вейвлет энергетическом спектру, а поэтому имеет зависимость от локализации спектральных характеристик сигналов.

АЭ нашла широкое применение при диагностировании конструкций и исследовании механизмов разрушения материалов. Важным фактором, используемым при идентификации сигналов АЭ, является определение места излучения сигналов АЭ. При этом источниками АЭ могут являться любые дефекты кристаллической, аморфной или композиционной структуры в твердом теле. Такими дефектами могут быть микро- и макротрещины, дислокации, двойники и др. Дефект при этом излучает упругую волну лишь в том случае, когда движется с переменной скоростью. Характеристики акустической волны, такие как: амплитуда, активность, энергия, частота, зависят от многих признаков и особенностей дефектов, их скоплений, материала и режима нагружения.