где x, y – декартовы координаты источника АЭ; xi, yi – декартовы координаты i-ого ПП; r – расстояние от источника АЭ до первого ПП, который предполагается ближайшим к источнику АЭ; v– скорость распространения сигнала; ti – задержка времени прихода сигнала к i-ому ПП.
Если используются полярные координаты, то система уравнений примет следующий вид:
![]() (3.1.2)
(3.1.2)
где ![]() – расстояния от источника АЭ до i-ого ПП; a, ai – углы места источника АЭ и i-ого
ПП.
– расстояния от источника АЭ до i-ого ПП; a, ai – углы места источника АЭ и i-ого
ПП.
Несмотря на то, что формулы (3.1.1) и (3.1.2) применимы для расчетов с использованием любого числа ПП, с произвольным их расположением на исследуемом материале, в алгоритме программы они никогда не используется: полученные с их помощью решения слишком громоздки и неприменимы для локации в реальном времени. Вместо этого выбираются частные случаи расположения датчиков и для них, с помощью формул (3.1.1) и (3.1.2), выводятся соответствующие уравнения измерений.
Расположение ПП, изображенное на рис. 3.1.6, в соответствии с формулой (1), дает следующую систему уравнений:
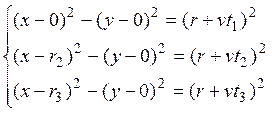
|
|
|
Рис. 3.1.6. Пример частного расположения ПП. |
Расположение приемников на одной линии позволяет «обнулить» величины y1, y2, y3, а совмещение первого ПП с началом координат - и величину x1. Система уравнений в полярных координатах выглядит ещё более компактно:
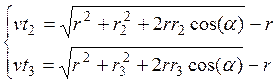
Ее решением является значение угла и расстояние от приемника до источника АЭ, с помощью которого нетрудно произвести расчет координат, перейдя к декартовым координатам:
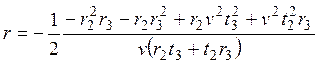 ,
,
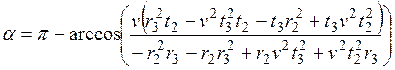
Эти выражения вполне подходят для расчетов в реальном времени, но, учитывая, что вычисления по этим выражениям будут производиться несколько сотен или даже тысяч раз в секунду, требуется проведение некоторой оптимизации. Например, нет смысла каждый раз перемножать расстояния между датчиками r2 и r3, которые являются постоянными величинами и т.п. Фактически, в выражениях для r и α переменными являются только значения задержек времени t, поэтому составляется таблица констант, куда заносятся все неоднократно повторяемые вычисления:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
… |
Теперь выражения оптимизированы для выполнения в качестве алгоритма компьютерной программы:
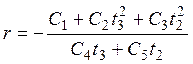 ,
,
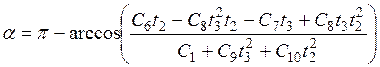
В программе Acoustic Emission Pro v2.0 имеется три возможные схемы расположения ПП: прямолинейная (была рассмотрена выше), L-образная и квадратная. В последних двух схемах используется 4 ПП.
Амплитуда сигналов АЭ, по мере их распространения в материале, уменьшается, что создаёт определенные трудности при их регистрации. Математически, амплитуда сигнала, удаленного на расстояние rот источника, выражается следующим образом:
![]()
где A– амплитуда сигнала на расстоянии rот источника; A0 – амплитуда сигнала в источнике; k– коэффициент затухания.
В алгоритме программы эта формула не применяется, вместо нее используется упрощающее предположение о равенстве расчетной временной задержки разности значений времени регистрации соответствующих пиковых значений амплитуд каждого из сигналов. Это приводит к небольшим погрешностям, но позволяет существенно сократить объем вычислений. Определение задержек времени является возможным благодаря наличию у АЦП двух буферов данных, позволяющих сохранять данные до и после наступления события. Превышение напряжения порога дискриминации Uп.д. отслеживается программой на канале, установленном в качестве источника триггера, и в некоторый момент наступает событие, запускающее процедуру считывания данных со всех каналов (на рис. 3.1.7. этот момент времени обозначен штриховой вертикальной линией). Далее определяются задержки времени прихода сигнала к ПП: для каждого из сигналов выделяются пиковые значения амплитуд и определяются разности соответствующих значений времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.