Анализ эволюции дефектной структуры поликристаллических материалов на различных стадиях нагружения методом акустической эмиссии (Постановка задачи, материал и методика исследований), страница 3

Для исследований были разработаны образцы специальной формы. Образец представляет собой балку равного сопротивления нагрузке и выполнен в виде пластины по форме равнобедренного треугольника (рис. 2.2.2).

Рис. 2.2.2 Чертеж образца для циклических испытаний на изгиб

При изгибе такой балки плоскопараллельные поверхности образца испытывают одинаковые напряжения растяжения/сжатия. При этом вероятность разрушения образца по всей рабочей части одинакова (не учитывая влияние на усталостную прочность других факторов). Схема нагружения балки равного сопротивления нагрузке приведена на рис. 2.2.3.

При определении прогиба для балки с переменным сечением необходимо помнить, что жесткость такой балки является функцией от х, поэтому дифференциальное уравнение изогнутой оси в упрощенном виде для балки, приведенной на рис. 2.2.3, принимает вид:

,

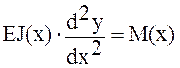где    J(х) – переменный момент инерции сечений балки, мм⁴;

М(х) – изгибающий момент, Н·мм.

Рис. 2.2.3 Схема нагружения балки постоянной толщины переменного сечения

Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту.

Изгибающий момент равен:

М(х) = Рх

Переменный момент инерции:

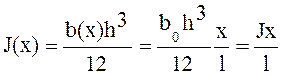
Тогда дифференциальное уравнение примет вид:

,

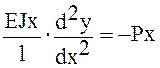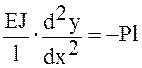
Проинтегрировав уравнение, получаем:

,

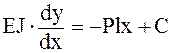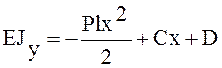
Для определения постоянных интегрирования имеем условия: в точке А при х = l прогиб у = 0 и угол поворота dy/dх = 0, или

0 = – Рl³ + С,

0 = – Рl³ + Сl + D

Тогда С = Рl³ и D = – Pl³/2.

Выражение для определения прогиба примет вид:

,

.

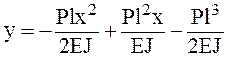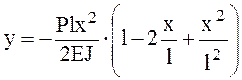Наибольший прогиб на свободном конце балки В получится при х = 0:

,

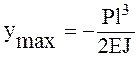где    у_max – прогиб, мм;

Р – нагрузка прикладываемая к образцу, Н;

l – длина образца, мм;

Е – модуль упругости Юнга, Па;

J – момент инерции, мм⁴.

Определим момент инерции для образца:

J = b₀h₀³/12,

где    J – момент инерции, мм⁴;

b₀ – ширина рабочей части образца в самой широкой области, мм;

h₀ – высота образца, мм.

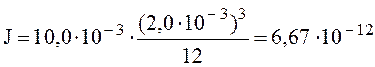
Подставим все значения в выражение прогиба и определим величину прогиба для образцов:

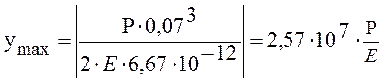               (2.2.1)

Определим напряжение:

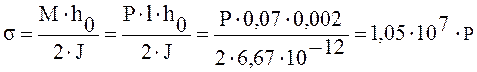         (2.2.2)

Формулы 2.2.1 и 2.2.2, с учетом влияния формы образцов в месте захвата в узкой части (рис. 2.2.2), были использованы для расчета значений прогиба и максимального напряжения s_max на поверхности образца изготовленного из материала с модулем Юнга Е при создании изгибающей нагрузки Р.

Гладкие образцы

Исследование особенностей эволюции дефектной структуры при циклическом нагружении гладких образцов проводилось на тех же материалах, что и при статическом растяжении. Ввиду большого объема практически проводимых циклических испытаний для каждого типа кристаллической структуры (ОЦК, ГЦК, ГПУ) были выбраны по одному представителю:

-  ОЦК кристаллическая решетка (сталь 20);

-  ГЦК кристаллическая решетка (алюминиевый сплав Д16АТ);

-  ГПУ кристаллическая решетка (титановый сплав ОТ4).

Образцы изготавливались путем электроэрозионной по контуру вырезки проволочным инструментом с максимально достижимой шероховатостью поверхности боковых граней Rz = 20.

Электроэрозионная обработка поверхности

Для исследования влияния шероховатости поверхности на кинетику накопления повреждений при формировании циклической усталости в материалах образцы сплава Д16АТ были подвергнуты поверхностной электроэрозионной обработке при различных значениях импульсного тока.

В результате электроэрозионной обработки образцов сплава Д16АТ на противоположных поверхностях образцов, испытывающих при изгибе максимальные напряжения растяжения/сжатия, была получена шероховатость:

Максимальный ток импульса обработки, А	3	12	18	33
Rz, мкм	54	90	122	137