Методы Рунге-Кутта (решение обыкновенных дифференциальных уравнений)

19. Методы Рунге-Кутта.(решение обыкновенных диф.уров.,)

Для решения задачи Коши Эйлером был описан метод, суть которого в том, что интервал [0,T] разбивается на подъынтервалов длительностью и на каждом k-ом подыинтервале в окрестности точки   искомое решение представляется в виде ряда Тейлора:

Полагая, что n=1, где n-порядок старшей производной в ряде Тейлора, получаем:

но и окончательно метод Эйлера имеет вид: (5.6)…………

Р-К: решение в (.) представляется в виде: (5.11) а есть некоторая функция, апроксимирующая отрезок ряда Тейлора, но не содержащая производных . Если через  p=n обозначить порядок точности метода(локальная погрешность ), то данная функция ищется в виде:

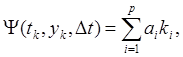
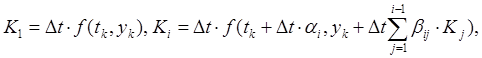
Коэффициенты  для заданного порядка точности p определяются из сравнения функции с р.Тейлора путем приравнивания коэффициентов при соответствующих слагаемых.

Для p=1 коэффициент ,и метод Р-К первого порядка точности

есть не что иное, как метод Эйлера.Локальная погрешность метода Р-К первого порядка точности пропорциональна , т.е.

Для p=2 коэффициент .,, а метод  Р-К второго порядка точности

Совпадает с модифицированным методом Эйлера.

Наиболее распространен метод Р-К четвертого порядка точности ,

,,

,Недостатком методов Р-К является их относительная сложность реализации, т.к. при определении , где рядок точности метода, на каждом шаге решения приходится неоднократно вычислять  для различных аргументов, а это может привести к накоплению выч. погр., особенно на длительных интервалах определения решения.