


Министерство образования Республики Беларусь
Кафедра высшей математики
«Решение систем линейных алгебраических
уравнений итерационными методами»
Выполнила: Проверила:
ст. гр. 551004 Ранцевич В.А.
Борисик В.О.
Минск, 2007![]()
1. Цель работы:
Изучить итерационные методы решения СЛАУ – метода простой итерации, метода Зейделя и метода Якоби; исследовать зависимость скорости сходимости метода простой итерации от требуемой точности, порядка системы и величины параметра итерации; сравнение скорости сходимости метода простой итерации и метода Зейделя и Якоби.
2. Исходная постановка задачи:
Написать программу, реализующую алгоритмы методов простой итерации, Зейделя и Якоби решения систем порядка n (n=10, 20, 40). Матрица СЛАУ для всех вариантов имеет вид:
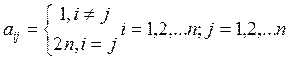
Вектор правой части СЛАУ зависит от порядка системы и имеет вид:
![]() .
.
В программе необходимо предусмотреть вычисление нормы матрицы и нормы невязки, вывод последней на каждой итерации, подсчет числа итераций. Вычисления продолжать до достижения заданной точности μ или до тех пор, пока число итераций не превысит 104. (μ=10-2, 10-4, 10-6 )
Окончание итерационного процесса происходит при выполнении одного из условий условия:
1)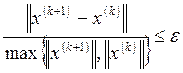 ,
,
2) 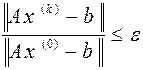 ,
,
3)
![]() .
.
В программе для окончания итерационного процесса использовалось условие 2.
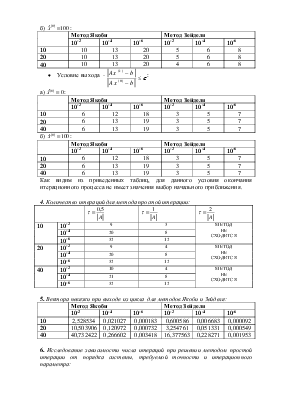
3. Количество итераций для методов Якоби и Зейделя:
· Условие выхода - 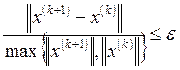 :
:
а)
![]() :
:
|
Метод Якоби |
Метод Зейделя |
|||||
|
10-2 |
10-4 |
10-6 |
10-2 |
10-4 |
10-6 |
|
|
10 |
5 |
7 |
10 |
3 |
3 |
4 |
|
20 |
5 |
8 |
12 |
3 |
4 |
5 |
|
25 |
5 |
8 |
12 |
3 |
4 |
5 |
б)
![]() :
:
|
Метод Якоби |
Метод Зейделя |
|||||
|
10-2 |
10-4 |
10-6 |
10-2 |
10-4 |
10-6 |
|
|
10 |
10 |
13 |
20 |
5 |
6 |
8 |
|
20 |
10 |
13 |
20 |
5 |
6 |
8 |
|
40 |
10 |
13 |
20 |
4 |
6 |
8 |
· Условие выхода - 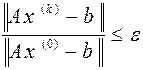 :
:
а)
![]() :
:
|
Метод Якоби |
Метод Зейделя |
|||||
|
10-2 |
10-4 |
10-6 |
10-2 |
10-4 |
10-6 |
|
|
10 |
6 |
12 |
18 |
3 |
5 |
7 |
|
20 |
6 |
13 |
19 |
3 |
5 |
7 |
|
40 |
6 |
13 |
19 |
3 |
5 |
7 |
б)
![]() :
:
|
Метод Якоби |
Метод Зейделя |
|||||
|
10-2 |
10-4 |
10-6 |
10-2 |
10-4 |
10-6 |
|
|
10 |
6 |
12 |
18 |
3 |
5 |
7 |
|
20 |
6 |
13 |
19 |
3 |
5 |
7 |
|
40 |
6 |
13 |
19 |
3 |
5 |
7 |
Как видим из приведенных таблиц, для данного условия окончания итерационного процесса не имеет значения выбор начального приближения.
4.Количество итераций для метода простой итерации:
|
|
|
|
||
|
10 |
10-2 |
9 |
3 |
МЕТОД НЕ СХОДИТСЯ |
|
10-4 |
20 |
8 |
||
|
10-6 |
32 |
12 |
||
|
20 |
10-2 |
9 |
4 |
МЕТОД НЕ СХОДИТСЯ |
|
10-4 |
20 |
8 |
||
|
10-6 |
32 |
12 |
||
|
40 |
10-2 |
10 |
4 |
МЕТОД НЕ СХОДИТСЯ |
|
10-4 |
21 |
8 |
||
|
10-6 |
32 |
12 |
||
5. Вектора невязки при выходе из цикла для методов Якоби и Зейделя:
|
Метод Якоби |
Метод Зейделя |
|||||
|
10-2 |
10-4 |
10-6 |
10-2 |
10-4 |
10-6 |
|
|
10 |
2,528534 |
0,021027 |
0,000183 |
0,600586 |
0,006683 |
0,000092 |
|
20 |
10,503906 |
0,120972 |
0,000732 |
3,254761 |
0,051331 |
0,000549 |
|
40 |
40,732422 |
0,266602 |
0,003418 |
16,377563 |
0,228271 |
0,001953 |
6. Исследование зависимости числа итераций при решении методом простой итерации от порядка системы, требуемой точности и итерационного параметра:
На основании полученных данных можно сделать вывод, что число итераций в методе простой итерации зависит от задаваемой точности и в гораздо меньшей мере от порядка системы.
Метод
простой итерации сходится при величине итерационного параметра 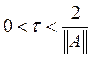 , что подтверждают полученные данные (при
итерционном параметре равном
, что подтверждают полученные данные (при
итерционном параметре равном ![]() метод не сходится, т.
е. число итераций превышает
метод не сходится, т.
е. число итераций превышает ![]() ). Скорость сходимости
метода больше при значении параметра, выбранного из середины указанного
интервала.
). Скорость сходимости
метода больше при значении параметра, выбранного из середины указанного
интервала.
7. Исследование зависимости числа итераций при решении методом простой итерации от порядка системы, требуемой точности и итерационного параметра:
Для метода Якоби можно сделать тот же вывод, что и для метода простой итерации: число итераций зависит и от задаваемой точности и гораздо меньше от порядка системы. Число итераций в методе Зейделя так же зависит от точности, но практически не зависит от порядка системы.
8. Проверка сходимости метода Зейделя со скоростью геометрической прогрессии и определение q:
Значения
q были
вычислены по формуле 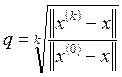 :
:
|
ε n |
10 |
20 |
40 |
|
0,01 |
0,28699 |
0,19492 |
0,11910 |
|
0,0001 |
0,28573 |
0,19359 |
0,11770 |
|
0,000001 |
0,28571 |
0,19355 |
0,11765 |
Получили значения q различными для различных размеров матрицы:
- для n=10 - ≈0,29;
- для n=20 - ≈0,19;
- для n=40 - ≈0,12.
Неравенство
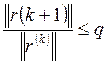 выполняется не при всех k=0,1,2,3...
. При точности 0,01 были получены следующие результаты:
выполняется не при всех k=0,1,2,3...
. При точности 0,01 были получены следующие результаты:
|
k n |
10 |
20 |
40 |
|
0 |
0,26345 |
0,28228 |
0,29958 |
|
1 |
0,13854 |
0,17167 |
0,19157 |
|
2 |
0,03788 |
0,05227 |
0,06932 |
Невыполнения
данного условия для метода Зейделя связано с тем, что при вычислении каждого ![]() используются уже полученные на этом шаге
значения
используются уже полученные на этом шаге
значения ![]() :
:
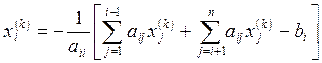 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.