



















































Построим математическую модель и попытаемся ее исследовать.
 |
Модель стохастическая, так как число тактов обрабатываемых МК в АЛУ величина случайная.
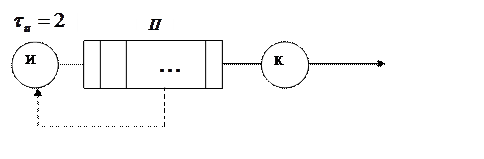
Считаем, что МК считывается каждые 2 такта.
Для описания интервалов обслуживания используем регулярный просеянный поток. Просеянный поток иногда называют дискретным пуассоновским, так как его свойства аналогичны для моментов вероятности кратным периоду Т.
 |
π - вероятность
того, что в момент ![]() событие не произойдет, (
событие не произойдет, (![]() ) -
вероятность того, что произойдет.
) -
вероятность того, что произойдет.
Какова вероятность того, что обслуживание окончится через i тактов?
![]() .
.
Средние значение времени обслуживания
![]()
![]()
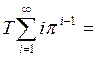
=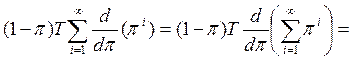
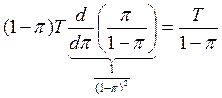 ;
;
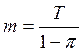 - математическое ожидание интервала
обслуживания.
- математическое ожидание интервала
обслуживания.
Это выражение соответствует геометрическому
распределению: 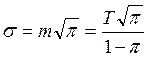 .
.
К просеянному регулярному потоку приводит, например регулярный поток данных , передаваемый по каналам связи с контролем наличия сбоев в передаваемом коде и исправлением путем повторной передачи.
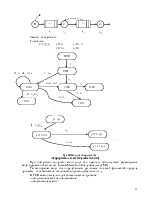
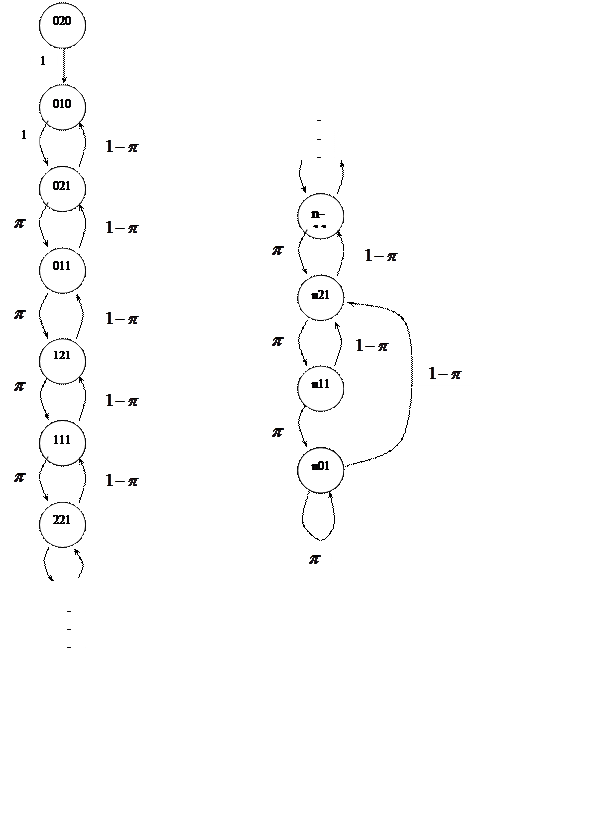
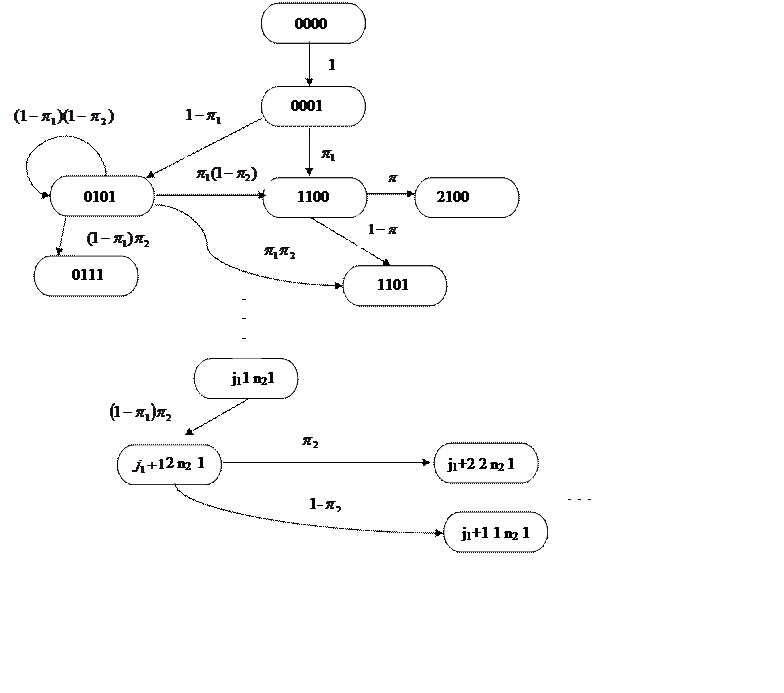
Построим граф переходов в цепи Маркова. Определим
состояние системы вектором, имеющим 3 компоненты: ![]() .
.
Временная составляющая t1 – число тактов,
 , оставшихся до появления заявки на выходе источника
(t1=0,
1, 2), 0 - если источник
заблокирован,
, оставшихся до появления заявки на выходе источника
(t1=0,
1, 2), 0 - если источник
заблокирован,
t2-время оставшееся до окончания обслуживания (возможное) заявки в АЛУ. t2 может принимать два значения:
t2=0-узел свободен;
t2=1-узел занят.
Комбинаторная составляющая j-количество заявок в накопителе.
Построим граф и систему уравнений для стационарных
(финальных) вероятностей состояний. P![]() .
.
В состояние P020 система больше не вернется, поэтому P020=0.
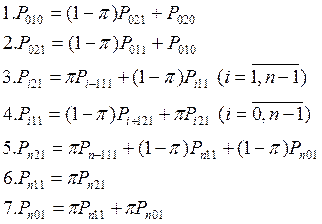
Обозначим ![]() ,
,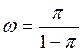 .
.
Тогда из 1 и 2 получим:
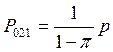 ,
,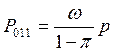 .
.
Проведя индукцию по i, будем иметь
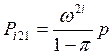
![]()
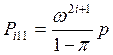
![]()
Из 6 и 7:
![]() ;
;
![]() .
.
Уравнение
5 превращается в тождество. Используя уравнение нормировки ![]() .
.
получим:
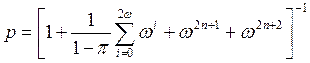 .
.
Отсюда, учитывая, что сумма- это сумма геометрической
прогрессии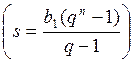 , получим
, получим
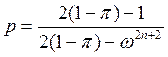 .
.
Используя полученное значение p (фактически, это вероятность простоя АЛУ) и рассчитав вероятности всех остальных состояний, можно найти другие интересующие нас характеристики системы.
Для просеянного потока математическое ожидание времени обслуживания каналом
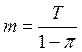 , Т- период просеивания.
, Т- период просеивания.
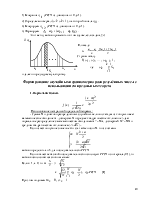
а) Определяем среднее время обслуживания заявки системы в целом (время пребывания) S.
Для достаточно большого интервала времени Тp - время на обслуживание в фазе обслуживания T*=Pобсл.Tp, где Pобсл.= ∑Pсост.обслуж.
Для одной заявки: SPобсл = m
Отсюда: S=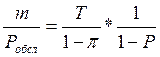
б) Какова интенсивность потока обработанных заявок
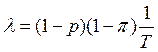
(1-p) – вероятность того, что канал обработал заявку.
(1-![]() ) – вероятность того,
что обработка закончилась.
) – вероятность того,
что обработка закончилась.
в) Средняя длина очереди
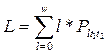
Пример 2.
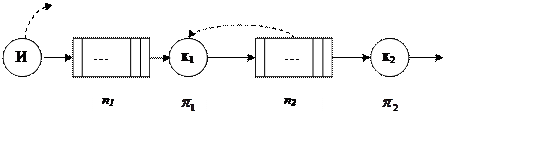 |
Заявка – каждый такт.
Состояние:
j1*t1*j2*t2 j1-0¸n1 t1-0, 1, 2
j1-0¸n2 t2-0, 1
Q-схемы (queuingsystem)
(непрерывно-стохастические модели)
При построении моделей такого рода как правило, используются рассмотрения моделируемых объектов, как Систем Массового Обслуживания (СМО).
Таким образом могут быть представлены различные по своей физической природе процессы – экономические, технические, производственные и т.д.
В СМО можно выделить два стохастических процесса:
-поступление заявок на обслуживание;
-обслуживание заявок.
Поток событий – последовательность событий, происходящих одно за другим в некоторые моменты времени. В СМО будем выделять два потока:
-входной поток: множество моментов времени поступления в систему заявок;
-поток обслуживания: множество моментов окончания обработки системой заявок.
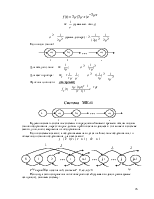
В общем случае СМО элементарного вида может быть представлено следующим образом

И Н К
Обслуживающий прибор
И – источник;
Н – накопитель;
К – канал обслуживания.
Поток событий однородный, если он характеризуется
только моментами поступления этих событий и задается последовательностью ![]() , где
, где
![]()
Поток
событий неоднородны, если он задается последовательностью ![]() ,
,
где
![]() - моменты поступления событий, а
- моменты поступления событий, а ![]() - набор признаков события (приоритеты
- набор признаков события (приоритеты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.