Лабораторная работа N3
ИССЛЕДОВАНИЕ УстойчивостИ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ
систем АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы: исследование устойчивости линейных САУ по ее математической модели. Анализ влияния отдельных параметров на ее устойчивость.
Порядок выполнения работы:
1. Записать математическую модель разомкнутой системы в tf-форме.
Transfer function: 5
-----------------------
0.01 s^3 + 0.52 s^2 + s
2.
Посмотреть вид переходного процесса (step),
логарифмические частотные характеристики (bode) на
выходе системы. Определить значение запаса устойчивости по фазе ![]() и значение запаса устойчивости по
амплитуде
и значение запаса устойчивости по
амплитуде ![]() (margin).
(margin).
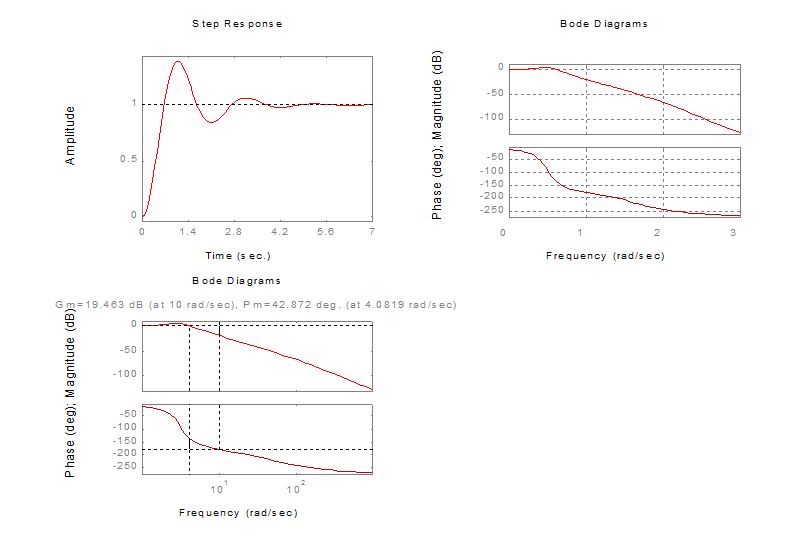
Определить
значение запаса устойчивости по фазе ![]() с помощью приближенного
соотношения по виду переходного процесса:
с помощью приближенного
соотношения по виду переходного процесса: ![]() =73 – Нm%, где Нm –
перерегулирование.
=73 – Нm%, где Нm –
перерегулирование.
3. Определить область устойчивости системы на плоскости параметров K,T1.
Матрица Гурвица выглядит следующим образом:
½1 T1*T2 0 ½
½K T1+T2 0 ½
½0 1 T1*T2½
D=T2+T1 – K*T1*T2 > 0 Þ К<1/T1+1/T2 ![]()
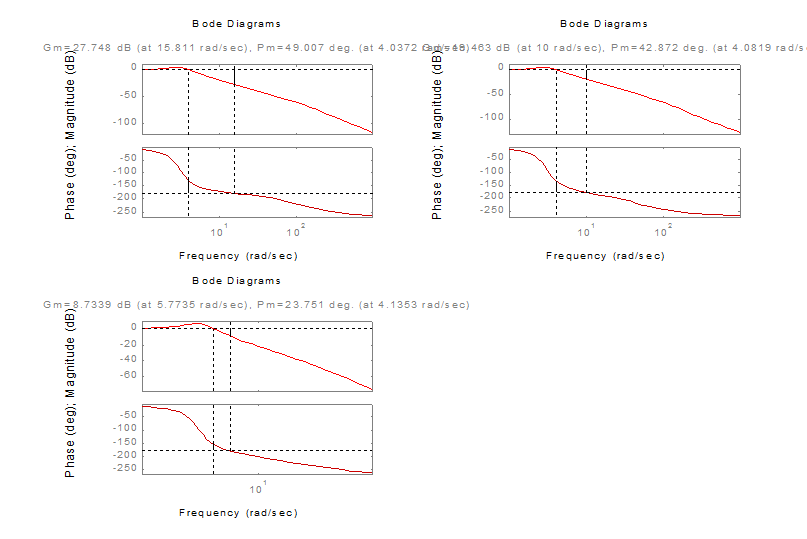
4. Исследовать зависимость запаса устойчивости по фазе от коэффициента усиления системы
 |
Примем К=1, К=5 и К=10.
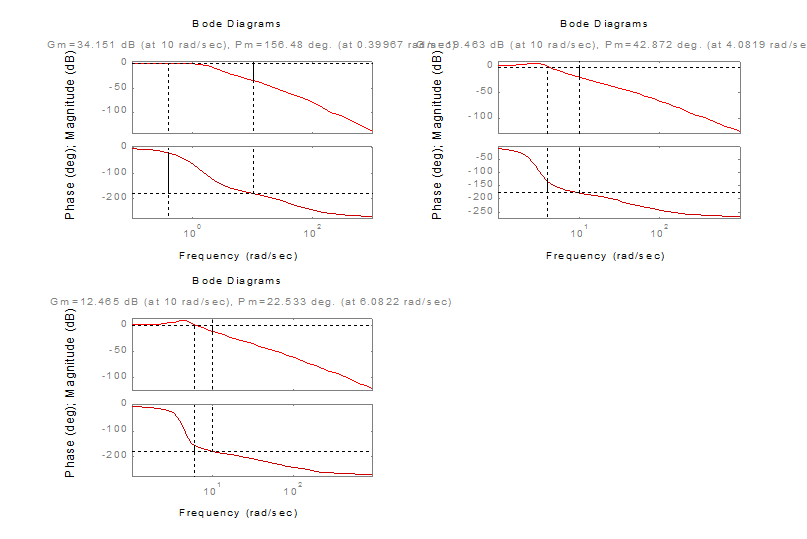
Вывод: при увеличении коэффициента усиления запас устойчивости по
фазе уменьшается.
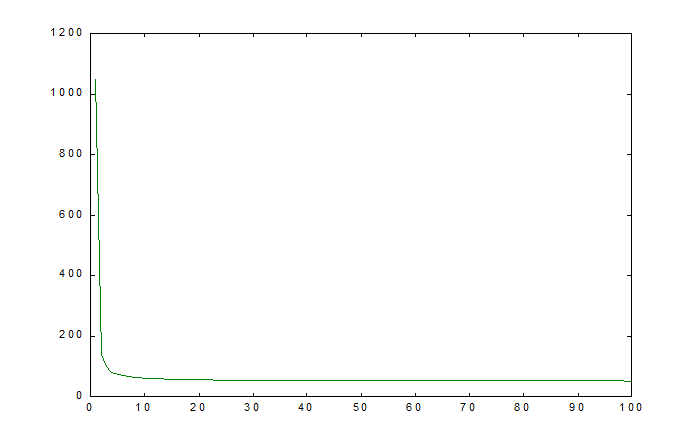
5.
Изменяя
коэффициент преобразования системы проследить изменение характера переходного
процесса. Определить значение коэффициента преобразования ![]() ,при котором система близка к потере
устойчивости.
,при котором система близка к потере
устойчивости.
Ккр=52.
6.
Снять зависимости запасов устойчивости по фазе и по амплитуде от изменения
других параметров системы ![]() ,
, ![]() ,
, ![]() .
.
Примем Т1=0,1; Т1=0,5 и Т1=1.
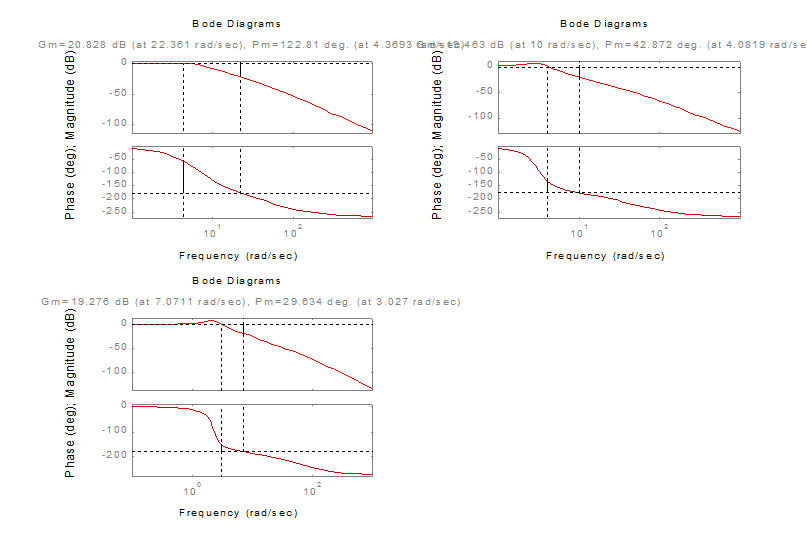
Примем Т2=0,008; Т2=0,02 и Т2=0,06.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.