Принятие решений в условиях частичной неопределенности, страница 2

1. Вычислим среднюю эффективность каждого решения по формуле

          .

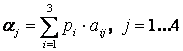2. Вычислим среднее квадратическое отклонение по формуле

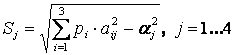
3. Вычислим средний риск

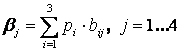
Результаты расчетов сведены в табл. 3.

Таблица 3.

Если рассматривать риск как недополучение дохода, т.е. по последнему столбцу, то наиболее выгодное решение – Р₃ (риск равен 0,2175), причем доходность здесь максимальная.

Если рассматривать риск как неопределенность (по третьему столбцу), то тогда наиболее выгодное решение с точки зрения минимизации риска – Р₁ (среднее квадратическое отклонение эффективности минимальное и равно 0,1064), но доходность здесь минимальная. Полученное выше решение с точки зрения неопределенности – самое неэффективное, т.к. имеем самую высокую неопределенность. Это же согласуется с основным принципом экономики: высокая прибыль – высокий риск, малый риск – низкая прибыль.