Создание и исследование моделей нелинейных нестационарных динамических систем (Лабораторная работа № 8)

Лабораторная Работа №8

Лабораторная работа состоит из двух частей. В настоящем файле приведены методические указания и варианты задания к первой части. Описание второй части приведено в файле Лабораторная Работа №8(часть2)

Часть 1

Создание и исследование моделей нелинейных нестационарных динамических систем

Цель работы: Получение навыков создания пользовательских моделей для визуального моделирования систем, описываемых дифференциальными, в том числе нелинейными нестационарными, системами уравнений.

Теоретические сведения

Система Simulink имеет в своем составе блок, называемый редактором дифференциальных уравнений (DEE). С помощью этого блока можно описать ОДУ или систему ОДУ в форме Коши, выполнить моделирование, получить расчетные функции в численном или графическом виде. Важно то, что DEE допускает описание и решение нелинейных нестационарных систем ДУ.

Работа с редактором выполняется следующим образом.

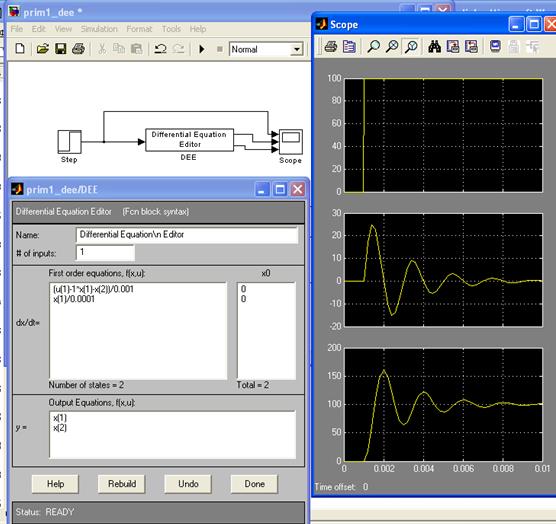
1.  Запускается DEE указанием имени редактора в окне команд системы Matlab

>> dee

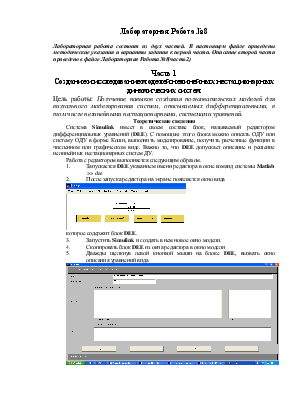
2.  После запуска редактора на экране появляется окно вида

которое содержит блок DEE.

3.  Запустить Simulink и создать в нем новое окно модели.

4.  Скопировать блок DEE из окна редактора в окно модели

5.  Дважды щелкнув левой кнопкой мыши на блоке DEE, вызвать окно описания уравнений вида

6.  Задать параметры для решения ОДУ или системы ОДУ, а именно:

- # ofinputs - количество варьируемых параметров на входе системы, т.е. параметров, значения которых будут поступать на вход блока DEE;

- x0 – задаются начальные условия для решения ОДУ;

- firstorderequations – задаются правые части дифференциальных уравнений, разрешенных относительно первых производных;

- outputequations – задаются переменные, которые будут являться решениями ОДУ.

7. В окне модели подать на вход блока DEE входные сигналы для варьируемых переменных, выходы блока DEE подключить к блоку, фиксирующему результаты моделирования в численном или графическом виде.

8. Запустить модель на выполнение.

Рассмотрим конкретные примеры применения блока DEE для решения ОДУ или систем ОДУ.

Пример 1.

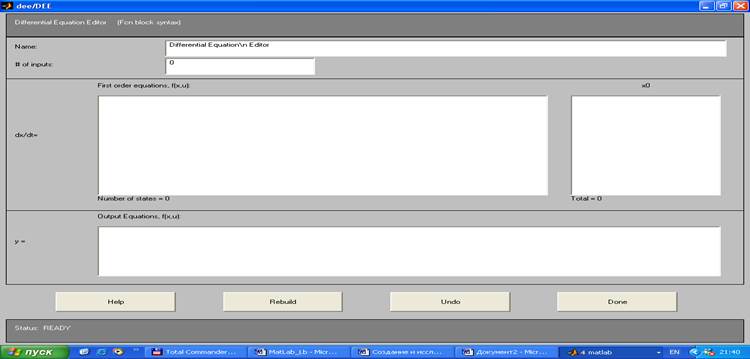
Смоделировать расчет переходного процесса в последовательном колебательном контуре, описанном системой дифференциальных уравнений вида:

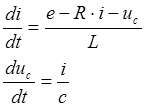
Для решения системы сделаем замену переменных, указанных в условии задачи,  на стандартные переменные DEE (стандартные переменные – x – для корней системы, u – для варьируемых входных параметров):

i – x(1)

u_c – x(2)

e – u(1)

После замены переменных система уравнений примет вид

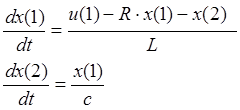
Выполним пункты 1-5 последовательности работы с DEE, в появившемся окне зададим вид системы уравнений, ее начальные условия.

Пример 2.

Смоделировать работу системы, имеющей 4 варьируемых параметра, описываемую дифференциальным уравнением вида:

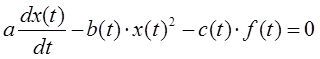
и имеющую блок обратной связи с некоторой передаточной функцией.

Приведем уравнение к форме Коши, получим:

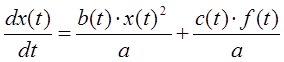
Выполним замену переменных:

a - u(1)

b(t) – u(2)

c(t) – u(3)

f(t) – u(4)

x(t) – x(1)

Тогда правая часть ОДУ примет вид:

u(2)/u(1)*x(1)^2 +u(3)/u(1)*u(4)

Последовательность создания модели такова:

1.  Выполним пункты 1-5 последовательности работы с DEE, в появившемся окне зададим вид уравнения, его начальное условие.

2.  Зададим нужные блоки для моделирования варьируемых параметров системы.

3.  Подадим результирующую функцию блока DEE на вход блока визуализации.

4.  Установим время моделирования 15 секунд и выполним моделирование. Убеждаемся, что система неустойчива. Если задать время моделирования более 30 секунд, то пакет не сможет выполнить моделирование, выдаст сообщение об ошибке.

5.  С помощью блока Transfer Fcn (раздел Continuous) зададим вид звена передаточной функции обратной связи: 2/(s+1).

6.  Установим время моделирования 40 сек. и запустим модель на выполнение. Схема модели, вид окна редактора DEE и результаты расчетов по модели приведены ниже.

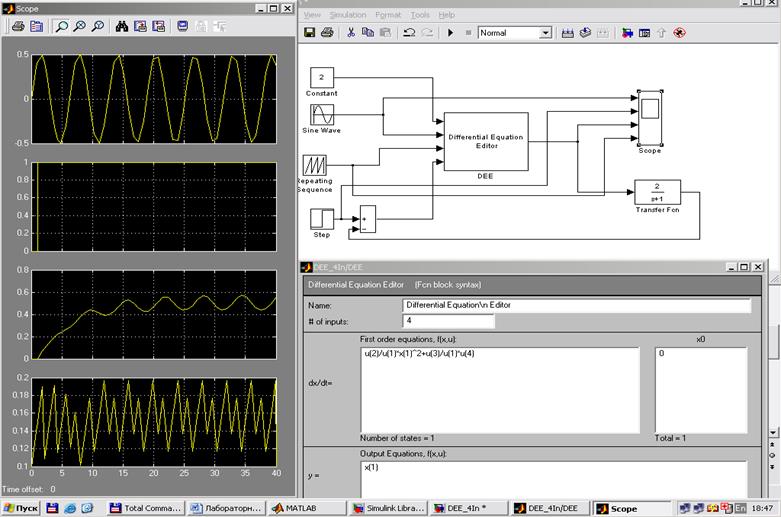
Наблюдаемый переходный процесс показывает (график 3), что при коэффициенте усиления звена обратной связи равном 2 система становится устойчивой.

Задание к лабораторной работе

1.  Описать в редакторе дифференциальных уравнений (DEE) пакета Simulink систему, описываемую следующим нестационарным нелинейным уравнением:

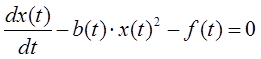
2. На вход блока подать варьируемые параметры:

Функцию b(t) задать в виде синусоиды, амплитуду задать равной  0.5, частоту сигнала задать 10 Гц;

Входной сигнал  задать в виде ступенчатой функции Step.

3.  Результирующую функцию (выход блока DEE), а также варьируемые параметры подать на выход блока визуализации SCOPE.

4.  Задать время моделирования 15 сек. и убедиться, что пакет не может выполнить моделирование.

5.  Задать время моделирования 7 сек. и выполнить анализ переходного процесса при указанных входных параметрах.

6.  С помощью блока Transfer Fcn (раздел Continuous) задать