Средства СКМ Maple для интерполирования и аппроксимации функций. Примеры и приёмы работы с функциями пакета stats

Средства СКМ Maple

для интерполирования и аппроксимации функций

Примеры и приёмы работы с  функциями пакета stats

> restart: 

> with ( plots ):  with (stats): with ( stats [statplots] ) :

Warning, the name changecoords has been redefined

Зададим массивы X и Y, в которые занесем соответственно абсциссы и ординаты некоторой исходной функции в пяти точках.

Подобный массив точек мы можем интерпретировать как исходные экспериментальные данные.

> X := [1, 2, 3, 4, 5] :

> Y := [0.1, 3, 0.2, 2, 6] :

Покажем точки массива на графике:

> scatterplot(X,Y) ;

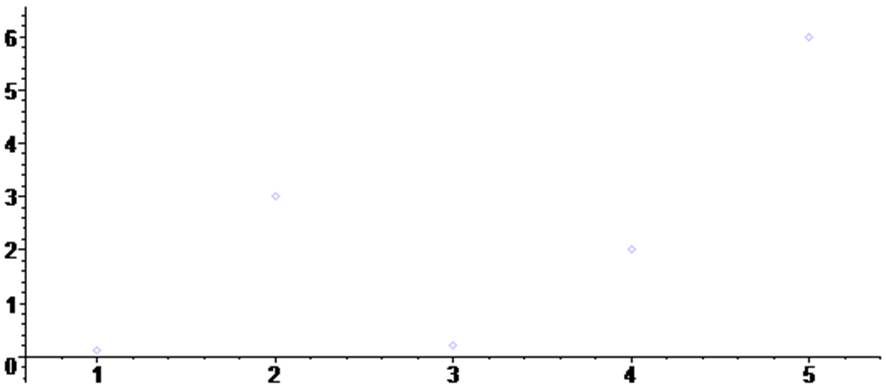
Далее получим интерполирующий полином, проходящий черех заданные точки, и построим его график.

> f := interp (X, Y, z) ;

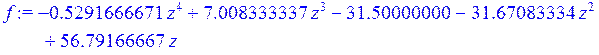
> g1 := plot (f, z = 1 .. 5) :

> g1;

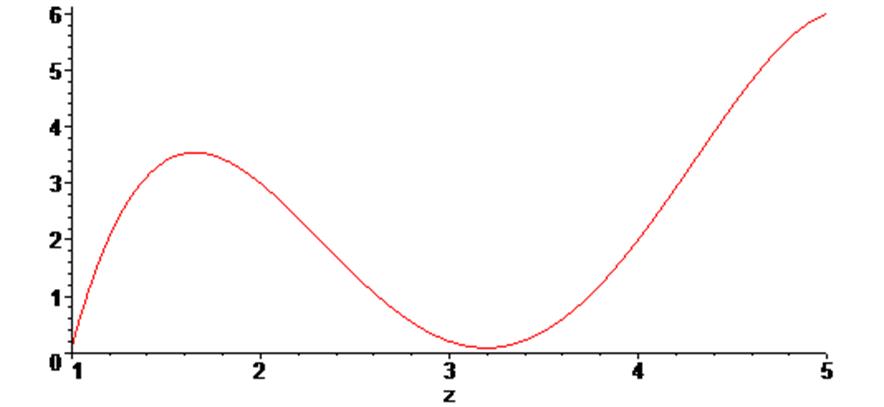
Ниже показан пример построения на одном поле вывода исходных точек и полиномиальной функции, которая проходит через них:

> plots [display] ( {scatterplot(X,Y) , g1} ) ;

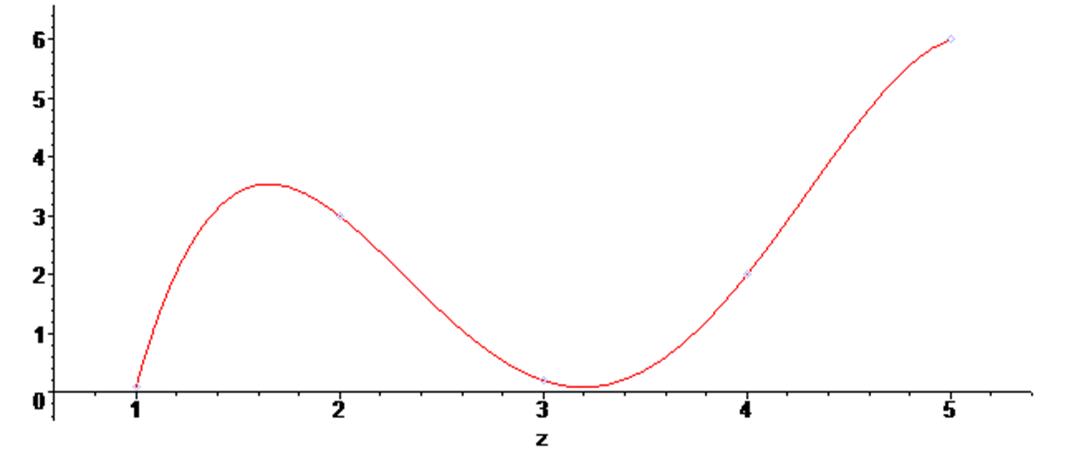
Далее приведён пример создания и построения графика пользовательской функции, которая является результатом полученной полиномиальной зависимости:

> f1 := unapply (f , z);

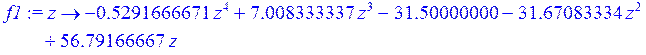
> g2 := plot (f1(z) , z = 1 .. 5) :

> g2;

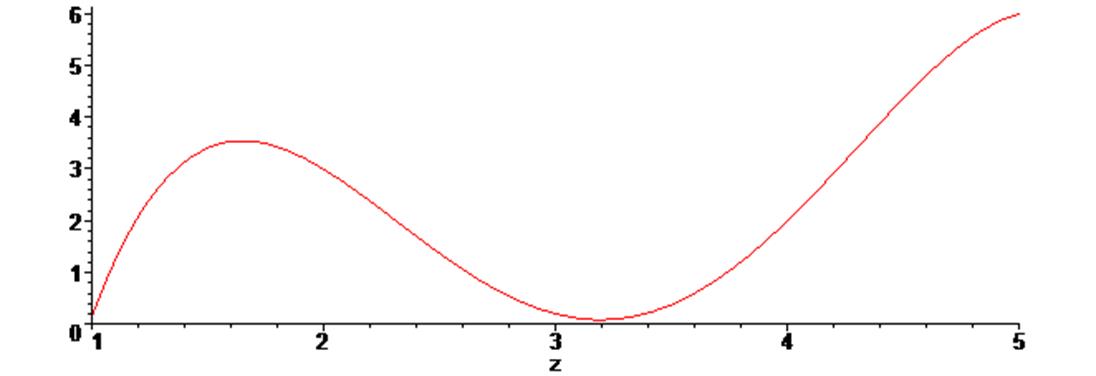
Увеличим число точек до 10-ти, получим интерполирующий полином, проходящий через них и построим его график :

> X1 := [0, 0.5, 1, 1.4, 1.9, 2.6, 3, 4, 4.5, 5] :

> Y1 := [0.1, 2, 1.9, 3, 2.7, 3.1, 3.9, 3.7, 4.1, 4] :

> f2 := interp (X1, Y1, z) ;

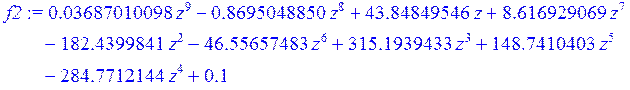
> g3 := plot (f2, z = 0 .. 5) :

> plots [display] ( {scatterplot(X1,Y1) , g3} ) ;

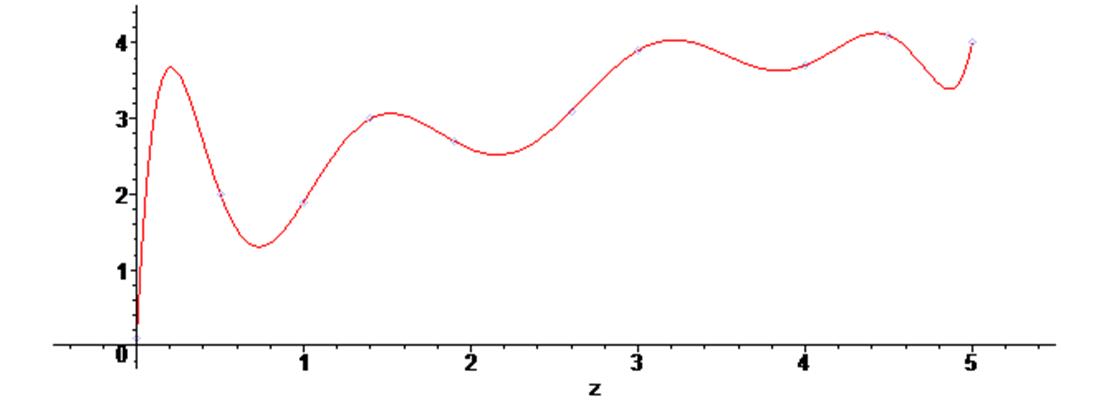
Как видим с увеличением степени полинома он начинает осциллировать, поэтому для большого числа точек с большим их разбросом не всегда удобно применять методы интерполирования данных. В подобных случаях применяют методы аппроксимации данных, т.е. методы регрессионного анализа. Эти методы позволяют провести некую усредненную кривую через заданные точки.

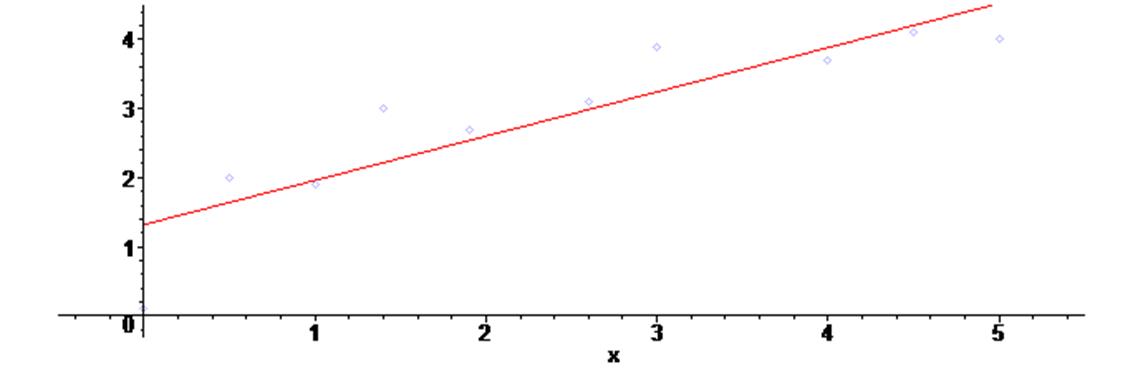
Ниже показаны примеры, на которых через массив точек из предыдущего примера проведены последовательно аппроксимирующие полиномы 1-го, 2-го и 3-го  порядка.

Для построения аппроксимирующих полиномов в примере использовалась функция leastsquare из пакета fit линейного регрессионного анализа

Как видим, полиномы второй и третьей степени дают для наших данных неплохие результаты усреднения.

> fa := fit [leastsquare [ [x,y], y = a*x +b ] ] ( [X1,Y1] ) ;

> assign (fa) :

> g4 := plot (y , x = 0 .. 5 ) :

> plots [display] ( {scatterplot(X1,Y1) , g4} ) ;

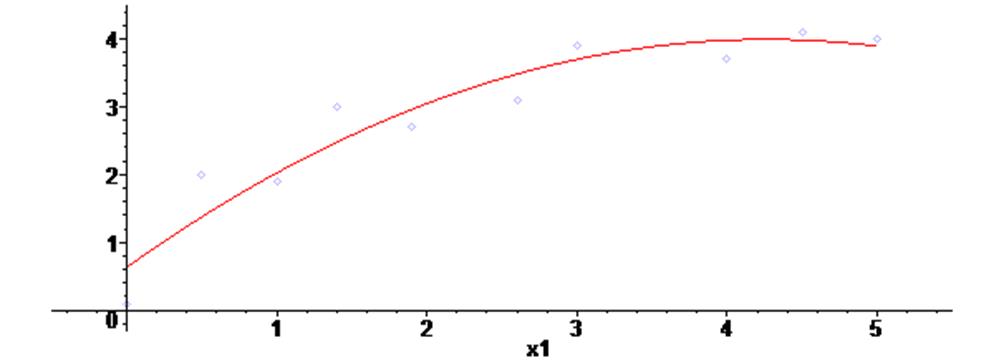
> fa1 := fit [leastsquare [ [x1,y1], y1 = a*x1^2 +b*x1 +c ] ] ( [X1,Y1] ) ;

> assign (fa1) :

> g5 := plot (y1 , x1 = 0 .. 5 ) :

> plots [display] ( {scatterplot(X1,Y1) , g5} ) ;

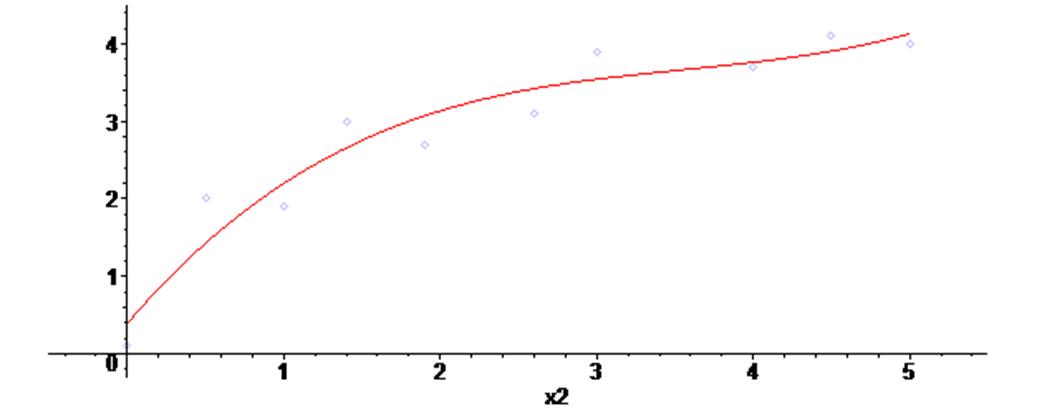
> fa2 := fit [leastsquare [ [x2,y2], y2 = a*x2^3 +b*x2^2 +c*x2 + d ] ] ( [X1,Y1] ) ;

> assign (fa2) :

> g6 := plot (y2 , x2 = 0 .. 5 ) :

> plots [display] ( {scatterplot(X1,Y1) , g6} ) ;

Выбор степени полинома определяется критерием, который должен сформулировать инженер.

Проведём теперь через заданные точки последовательно линейный и кубический сплайн:

> Sl := spline ( X1, Y1 , x, linear) ;

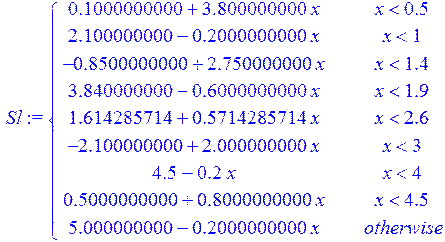
> g7 := plot (Sl , x = 0 .. 5 ) :

> plots [display] ( {scatterplot(X1,Y1) , g7} ) ;

> Sс := spline ( X1, Y1 , x, 3) ;

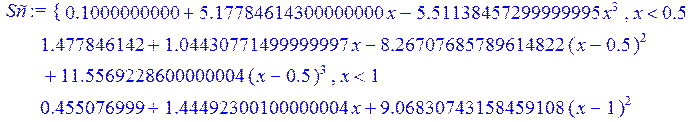
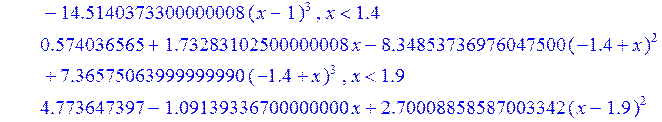
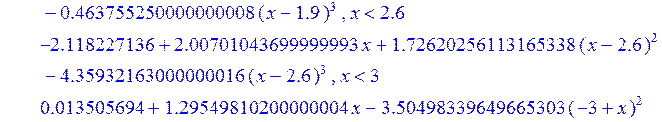
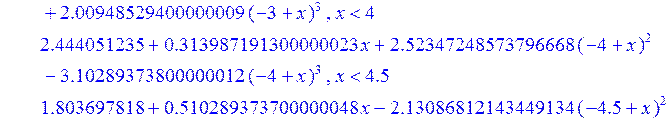
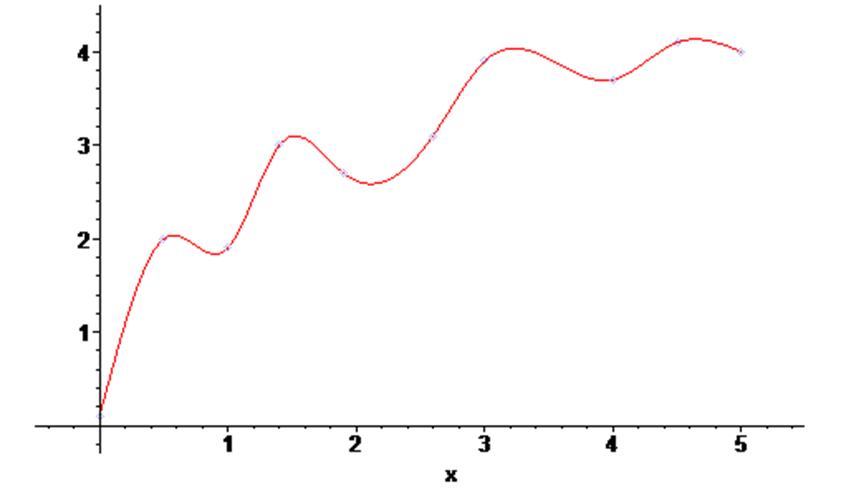
> g8 := plot (Sс , x = 0 .. 5 ) :

> plots [display] ( {scatterplot(X1,Y1) , g8} ) ;

Генерация случайных чисел с заданными параметрами

Для генерации  случайных чисел в системе компьютерной математики Maple используется функция random пакета stats.

В Maple возможно задание практически всех необходимых в инженерной практике дискретных и непрерывных распределений.

Примеры её использования приведены ниже.

Генерация пяти случайных чисел по нормальному и равномерному законам распределения.

Параметры законов распределения оставим "по умолчанию".

Число в скобках - количество генерируемых чисел.

> stats [random , normald] (5) ;

> stats [random , uniform] (5) ;

Покажем пример генерации ста случайных чисел по  равномерному и нормальному законам и записи их  в массив.

 Выведем графики массивов и сравним результаты.

> R := array (1 .. 100) :

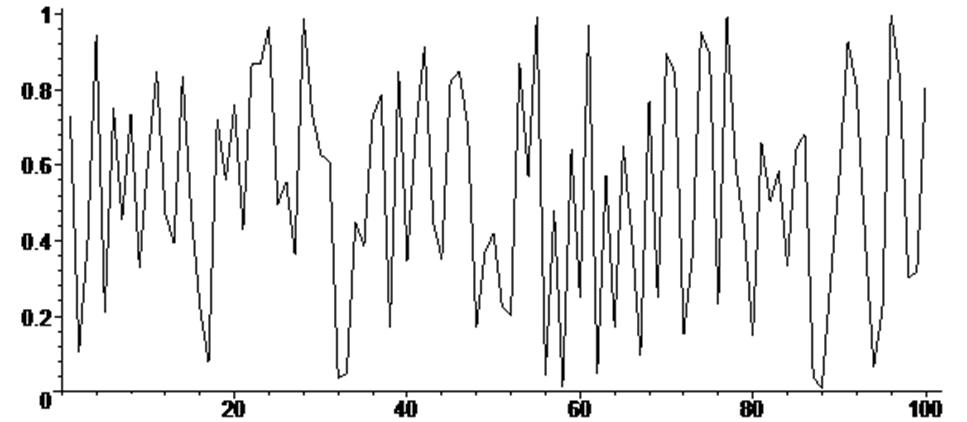
> for i from 1 by 1 to 100 do R[i] := stats [random , uniform] (1) end do :

> listplot ( [seq ( [i , R[i]] , i = 1 .. 100 ) ] ) ;

> for i from 1 by 1 to 100 do R[i] := stats [random , normald] (1) end do :

> listplot ( [seq ( [i , R[i]] , i = 1 .. 100 ) ] ) ;

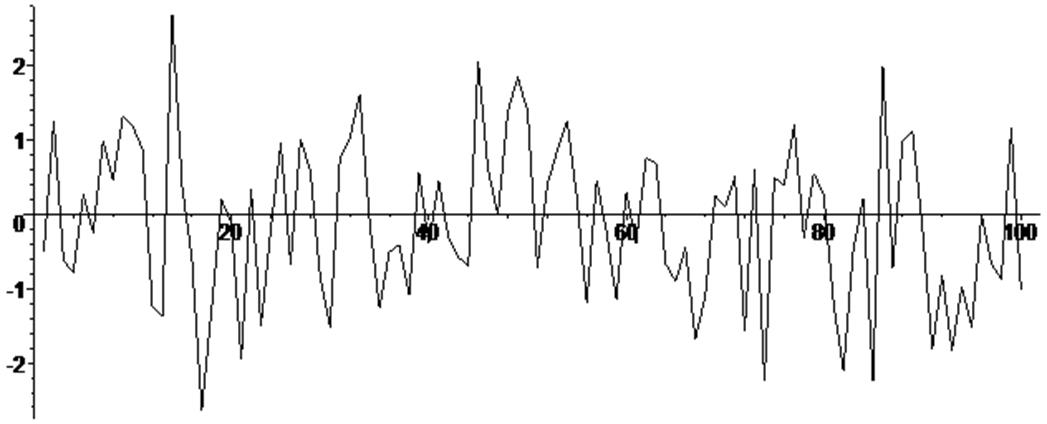
Особо следует обратить внимание на диапазоны  чисел, генерируемых при неуправляемых опциях!