Сертификация систем железнодорожной автоматики на безопасность

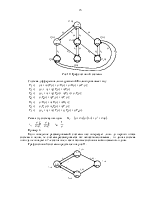
вероятности нахождения восстанавливаемой вычислительной системы в любом из  возможных ее состояний в произвольный момент времени Р_i(t):

Табл.1

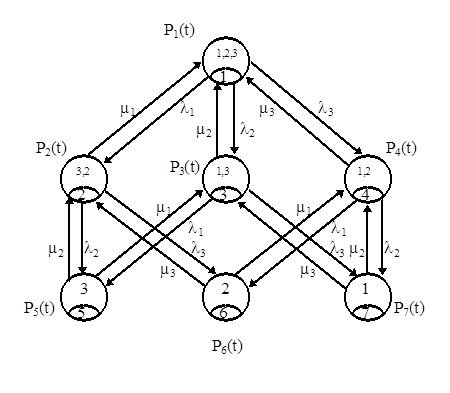
Рис.8. Граф состояний, отражающий износ вычислительной системы

Или иначе:

Решаем систему дифференциальных уравнений с учетом условия задачи, что в момент первоначального включения системы все мЭВМ исправны, т.е.  Р₁(0) = 1, а  Р₂(0) = Р₃(0) = Р₄(0) = Р₅(0) = Р₆(0) = Р₇(0) = 0. Учитывая , что l₁=l₂=l₃=l; m₁=m₂=m₃=m и ту особенность нахождения К_г(t), К_г, t_ср, t_в что в процессе их вычисления не обязательно знать отдельно функции  всех вероятностей Р_i(t) , а достаточно знать функции сумм вероятностей нахождения системы в исправных и отказовых состояниях, т.е.

систему можно упростить:

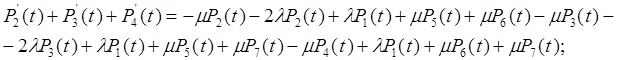
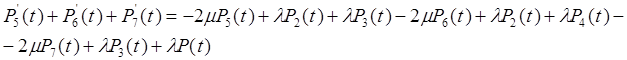
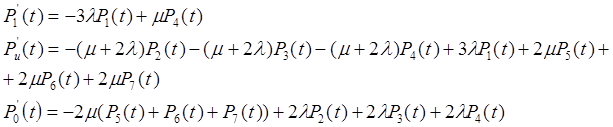
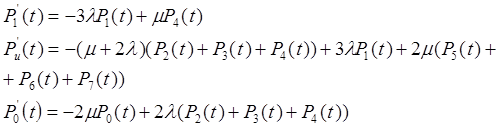
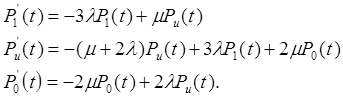
Упрощенной системе соответствует граф, представленный на рис.9.

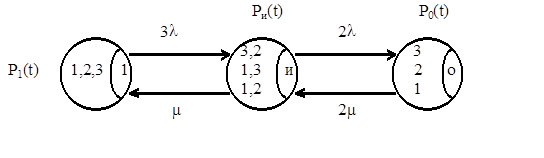
Рис.9. Граф состояний упрощенной системе

Функции вероятности Р₁(t), Р_u(t), Р_о(t) определяем , применяя преобразование Лапласа к системе уравнений при начальных условиях  Р₁(0) = 1,  Р_u(0) = 0, Р_о(0) = 0.

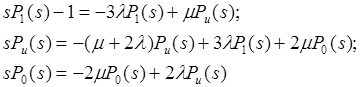
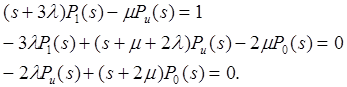
Решая систему алгебраических уравнений, находим изображения вероятностей:

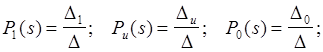
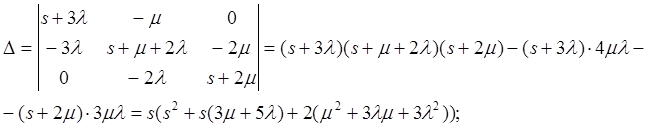
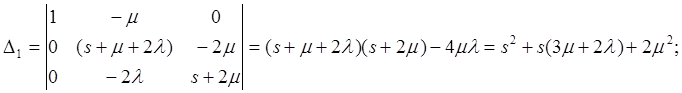
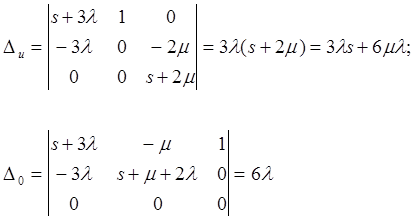
Имеем:

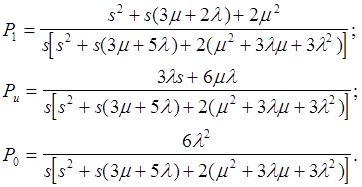
Вычисляем  функцию готовности:

                           К_г(t) = 1 - Р_о(t)

Функцию Р_о(t) определяем, применяя обратное преобразование Лапласа:

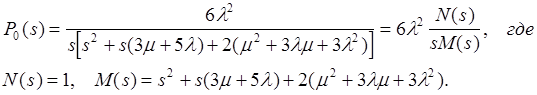
Тогда:

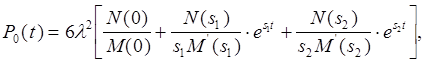
где  N(0) = N(S₁) = N(S₂) = 1;

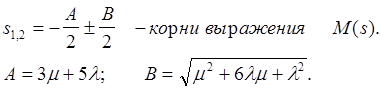
т.е. функция вероятности нахождения системы в состоянии отказа равна:

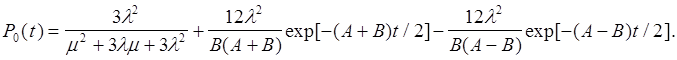
Найдем функцию готовности системы:

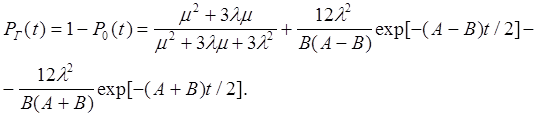
Коэффициент готовности:

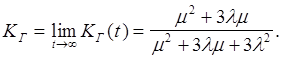
Среднее время наработки между отказами t_ср:

где финальные вероятности нахождения системы в состояниях "1","u", "0" соответственно равны:

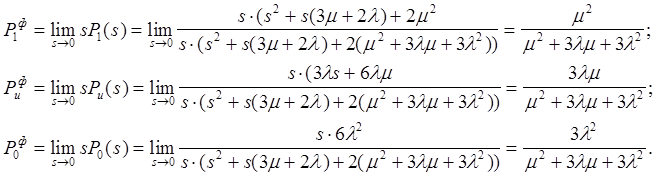
Тогда подставив значения получим:

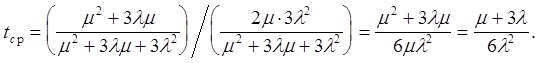
Среднее время восстановления системы t_в можно найти из соотношения :

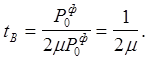
Пример 2. 

Определим К_г для этой же системы, при условии, что резервная мЭВМ  используется в режиме ненагруженного скользящего резерва и система обслуживается одной ремонтной бригадой в порядке прямого приоритета.

Составляем таблицу состояний (табл.2).

Табл.2

Строим граф состояний (рис.10).

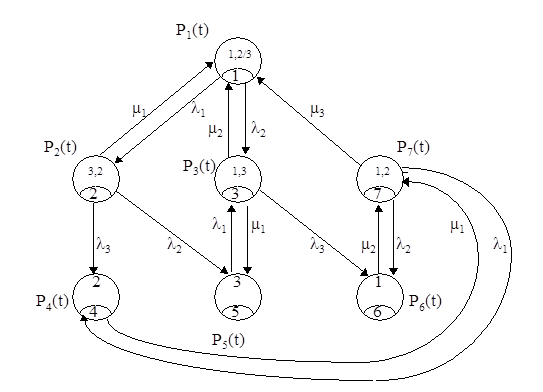
Рис.10. Граф состояний системы

Система дифференциальных уравнений Колмогорова имеет вид:

Решая эту систему находим      

Пример 3.

Если поведение рассматриваемой системы нас интересует лишь до первого отказа системы в целом, т.е. система рассматривается как невосстанавливаемая ,  то данная система никогда не попадает в 7-е состояние, и все отказовые состояния можно заменить одним.

Граф состояний системы представлен на рис.11.

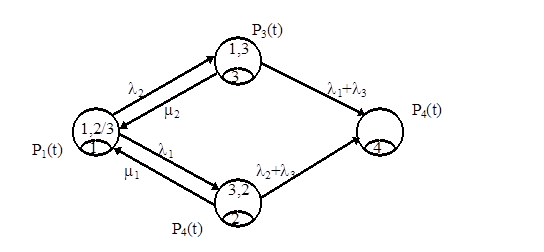
Рис.11. Граф состояний системы

Система дифференциальных уравнений Колмогорова имеет вид:

Решая систему можно вычислить наработку на отказ системы:

Пути повышения надежности и безопасности МИУС

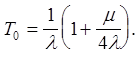
Надежность ИУВС растет по мере совершенствования элементной базы. В частности, применение МП наборов БИС, БИС ЗУ ведет к уменьшению числа элементов и межсоединений ( паек, сварок ) в средствах вычислительной техники. Одна- ко из-за тенденции постоянного увеличения  функциональных возможностей средств вычислительной техники число элементов в системах остается достаточно большим.

Если резерв в ИУВС отсутствует, то практически невозможно достичь приемлемых показателей надежности. Так как в инженерной практике считают, что  вычислительное средство надежно, если в течение некоторого интервала времени Dt вероятность безотказной работы Р(t) >=0,997 , то при l=10^-4-10^-7 1/ч и числе элементов в системе n=10^-4-10^-5 время безотказной работы в указанном выше смысле составляет лишь  единицы часов:

При l=10^-7 и n=10⁴ - Dt=3ч. Так как существенно уменьшить n и l нельзя, то и увеличить Dt без  применения резерва практически не  удается