Решение нелинейных уравнений (Решение уравнения 3х-6ln(х)-5 с точностью E=0.00001), страница 2

Дано: a,b([a-b]>=0.1)-значение, полученное в разделе 1.

F (x) = 3x-6ln(x)-5     е=10^-5  

     Найти x,a,b.[a,b] в цикле делится пополам (x=(a+b)/2).

Деление отрезка пополам происходит до тех пор, пока расстояние между значениями a,b не станет         меньше e.

   Корнем уравнения с точностью e является любое значение х на интервале [a,b]-есть корень уравнения. Нахождение х, при котором F(x) стремится к 0 называется уточнением корней уравнения.

2.2 Программа на языке Pascal и результаты уточнения корней

Program RGR;

var x,yx,ya,a,b,eps:real; fp:text;

procedure F(x:real; var y:real);

begin

  y:=3*x-6*ln(x)-5;

end;

begin

   assign (fp,'d:\tp\bin\mg11\kvv\dfkz1.txt');

   rewrite (fp);

   write ('Vvedi a,b,eps=');  readln (a,b,eps);

   repeat

     F(a,ya); x:=(a+b)/2;  F(x,yx);

     if ya*yx>0  then a:=x  else b:=x;

   until  abs(b-a)<eps;

   writeln (fp,'x=',x:9:6,'     y=',yx:9:6);

   close(fp);

end.

Результат работы программы

x= 0.581104     y= 0.000269

x= 4.806689     y= 0.000017

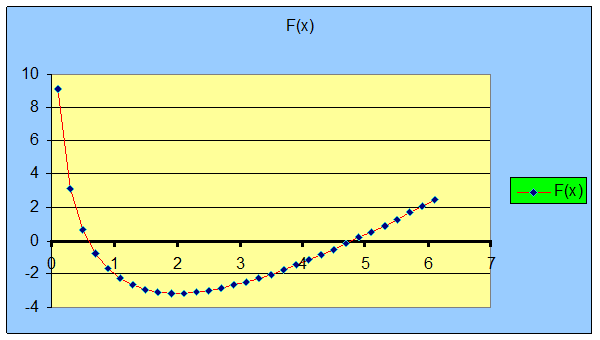
4. Решение уравнения с помощью табличного процессора Excel

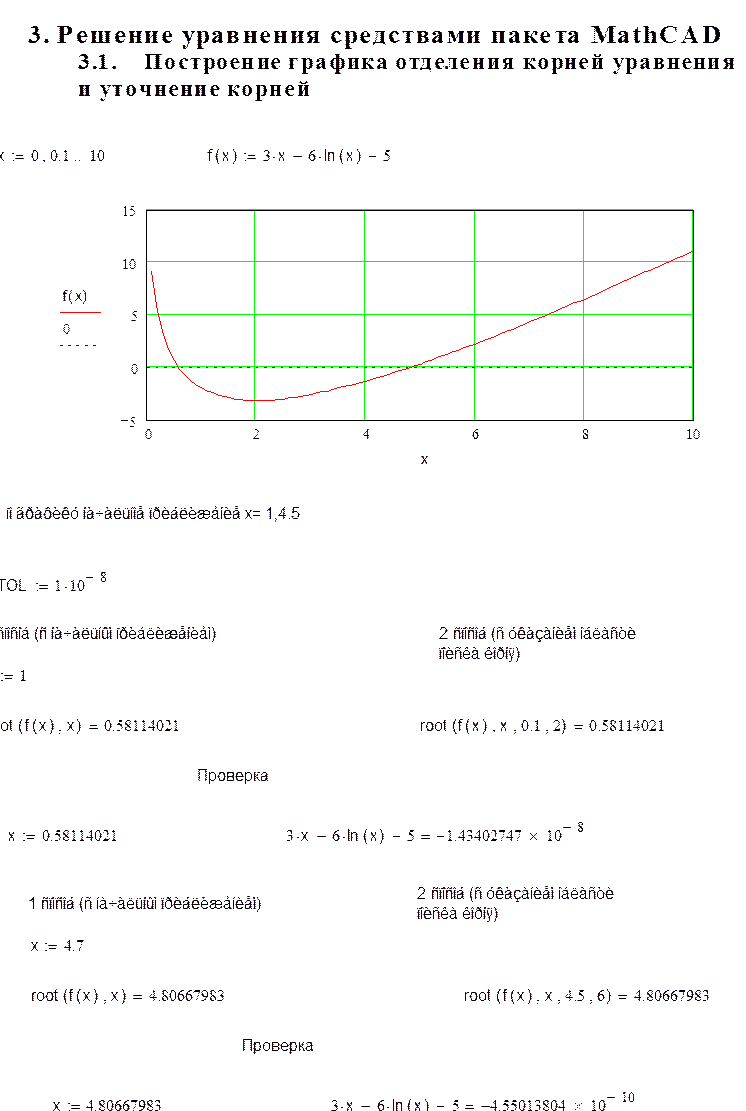
4.1 Построение графика функции уравнения и уточнение корней уравнения

	f(x)=3*x-6ln(x)-5
х	F(x)
0,1	9,115511
0,3	3,123837
0,5	0,658883
0,7	-0,75995
0,9	-1,66784
1,1	-2,27186
1,3	-2,67419
1,5	-2,93279
1,7	-3,08377		Уточнение корней
1,9	-3,15112		Корень1	Х1
2,1	-3,15162		0,581142	-1,5E-05
2,3	-3,09745
2,5	-2,99774		Корень2	Х2
2,7	-2,85951		4,807169	0,000857
2,9	-2,68826
3,1	-2,48841
3,3	-2,26353
3,5	-2,01658
3,7	-1,75
3,9	-1,46586
4,1	-1,16592
4,3	-0,85169
4,5	-0,52446
4,7	-0,18538
4,9	0,164589
5,1	0,524557
5,3	0,893759
5,5	1,271511
5,7	1,657203
5,9	2,050286
6,1	2,450267

Вывод.

   В результате выполнения расчетно-графической работы  по дисциплине “Информатика” я получила навыки работы с персональным компьютером, научилась работать с текстовым  редактором  Microsoft Word, с математическим пакетом MathCad,а также научилась  работать в Borland Pasсal for Windows.

   В процессе работы изучила метод уточнения корней, а именно метод половинного деления и отделение корней уравнения на большом интервале [a1;b1] с  шагом h.

   В пакете MathCad выполнила трассировку метода половинного деления по трем итерациям на некотором интервале, построила график функции и уточнила корни с помощью MathCad’а.

При работе использовала нижеуказанный список литературы.

8

Литература

   1 Валвачов А.Н., Крисевич В.С. «Программирование на языке Pascal для ПЭВМ», Минск, «Высшая математика», 1989.

    2 Гурин Н.Н. «Работа на персональном компьютере», Минск, «Беларусь»,1994.

    3 Ершова Н.М., Акулов Н.В. «Лабораторный практикум на ПЭВМ по исследованию математических моделей подвижного состава», Гомель, БелГУТ, 1994.

    4 Кушнеренко А.Г. «Основы информатики и вычислительной техники», Москва, «Просвещение», 1992.

    5 Очков В.О. «MathCAD+6.0 для студентов и инженеров», Москва, «Компьютер Пресс», 1996.

   6 Сементовский А.В. «Численные методы решения задач на ЭВМ», Гомель, БелГУТ, 1996.

                                          

9