Расчёт магнитной цепи постоянного тока (с заданным числом витков: W1=500, W2=600). Шифр 108, страница 2

Исходные данные:

                   

       

                           

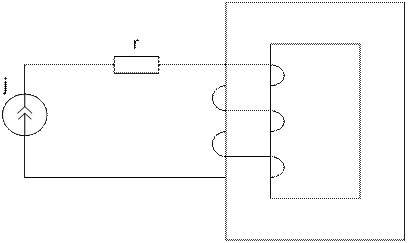
Рисунок 1 – Схема цепи

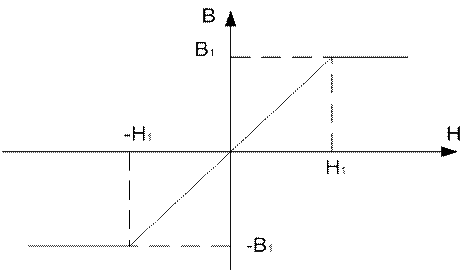
Рисунок 2 – Кривая намагничивания

1. Построим вебер-амперную характеристику катушки:

Перейдем от кривой намагниченности   к вебер-амперной характеристике . Для чего определим  и .

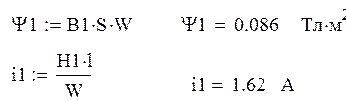
Вебер-амперная характеристика катушки будет иметь вид:

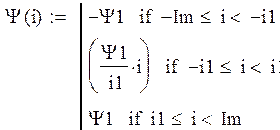
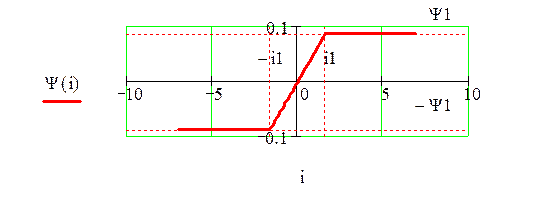
Рисунок 3 – Вебер-амперная характеристика катушки

2. Построим графики зависимости потокосцепления , напряжений на резисторе , катушке  и зажимах источника тока  в функции .

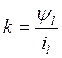Так как на участке от  до  , где , то .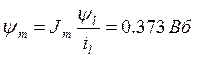

Определим угол отсечки:

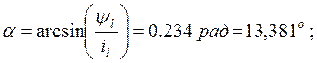
Проверим правильность нахождения угла отсечки:

Построим график :

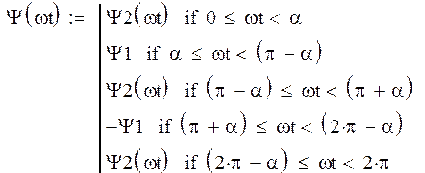
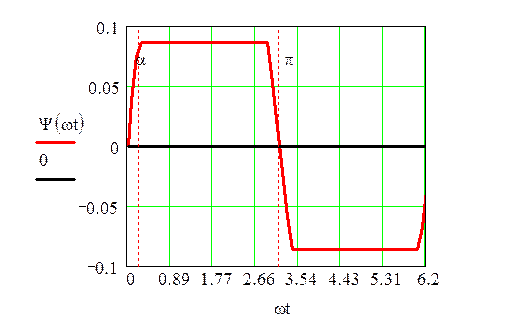
Рисунок 4 – График функции

Найдем напряжение на катушке:

Так как напряжение на катушке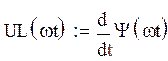, то получаем:

Построим график напряжения на катушке:

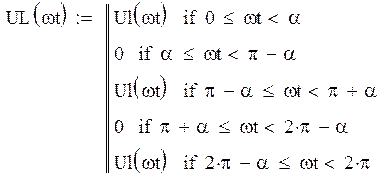
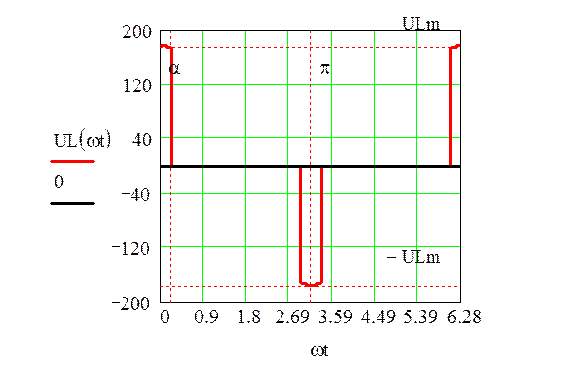
Рисунок 5 – График напряжения на катушке

Найдем напряжение на резисторе:

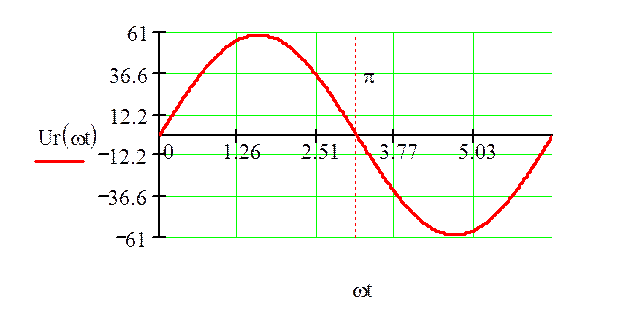
Рисунок 6 – График напряжения на резисторе

Построим график напряжения на зажимах источника тока:

Рисунок 7 – График напряжения на зажимах источника тока

3. Найдем аналитически действующие значения напряжений на элементах цепи: , и .

Найдем действующее значение напряжения на катушке:

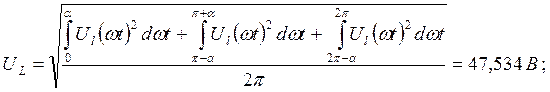
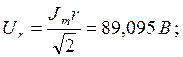
Так как сдвиг фаз между  и  равен , то:

4. Рассчитаем действующие значения , и  символическим методом по первой гармонике кривой .

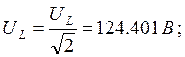
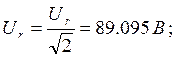
Задача №3

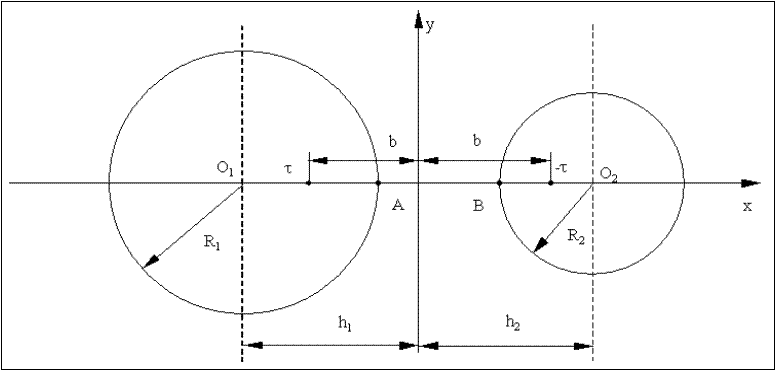
1. Для заданной схемы двух параллельных цилиндров (рисунок ниже), имеющих разные заряды противоположного знака q = (q1 = -q2), определить:

а) напряжение

б) ёмкость

2. Построить графическую картину электростатического поля, соблюдая следующие требования:

а) разность потенциалов между двумя любыми соседними линиями равного потенциала должна быть одна и та же;

б) поток вектора напряженности электростатического поля во всех силовых трубках должен быть одинаков;

в) при построении картины поля на каждой линии равного потенциала указать значение потенциала.

3. Вычислить и представить в виде графиков изменение потенциала и напряженности электростатического поля на линии, соединяющей наиболее близкие точки цилиндров, и распределение плотности заряда на поверхности цилиндра меньшего радиуса. 

 

1). Определим h1 и h2 - расстояния от геометрических цилиндров до плоскости

нулевого потенциала, а также b - расстояние  от  электрических  осей  до  этой

плоскости:

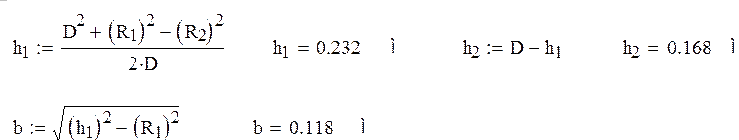
2). Определим коэффициенты k1 и k2, где k1 - значение отношения r2/r1 для точки А, а k2- соответственно для B. (r2 - расстояние от рассматриваемой точки до электрической оси цилиндра - t, а r1 - соответственно до t):

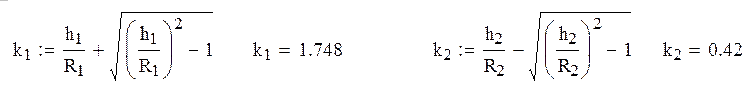
3). Емкость между цилиндрами равна:

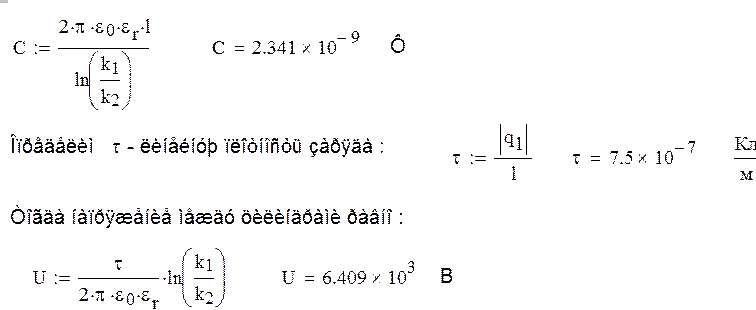
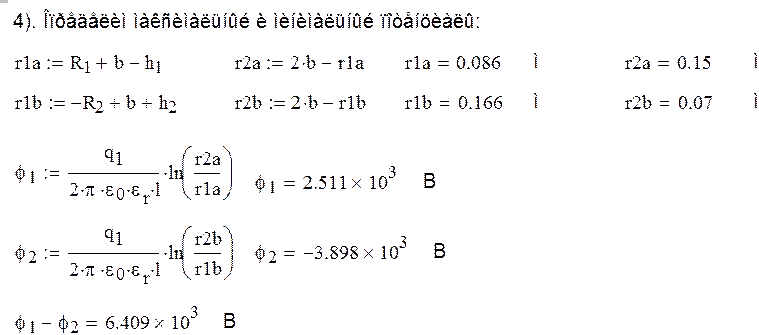
II. Рассчитаем и построим графическую картину электростатического поля двух

     цилиндров:

1). Найдём уравнения линий равного потенциала:

Уравнение любой линии равного потенциала имеет вид:

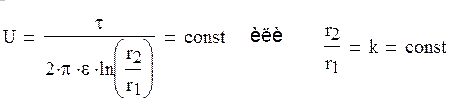
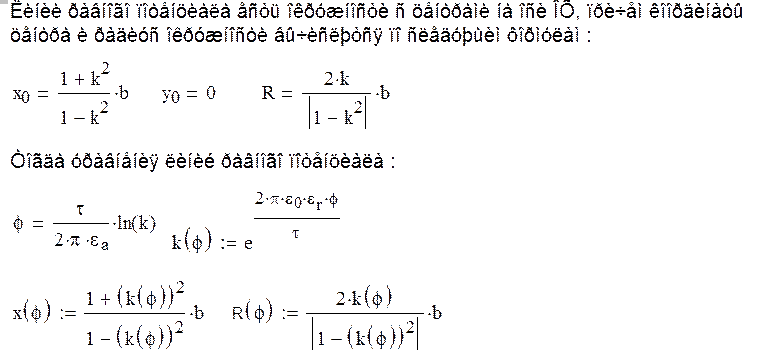
2). Найдём линии напряжённости поля:

Уравнение любой линии напряженности поля для потока вектора напряженности поля имеет форму:

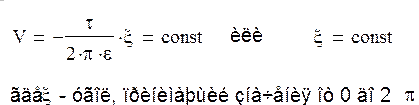
Следовательно, уравнение любой линии напряженности поля - есть окружность пересекающаяся с электрическими осями  t и -t с центром, координаты которого определим по формулам:

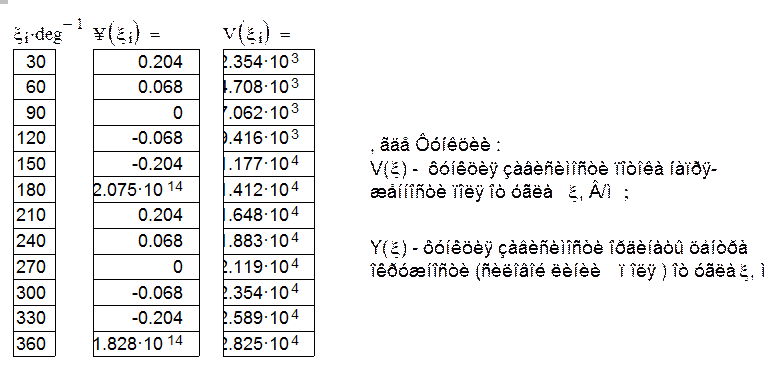 III. Вычислим и построим в виде графиков:

     1). Изменение потенциала электростатического поля на линии, соединяющей наиболее близкие точки цилиндров:

Потенциал в некоторой точке, удалённой на расстояния r1 и r2 от электрических осей цилиндров, определяется по формуле: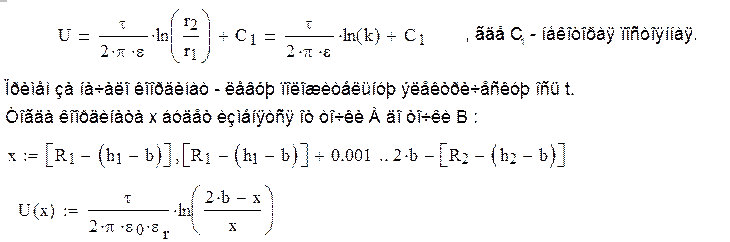

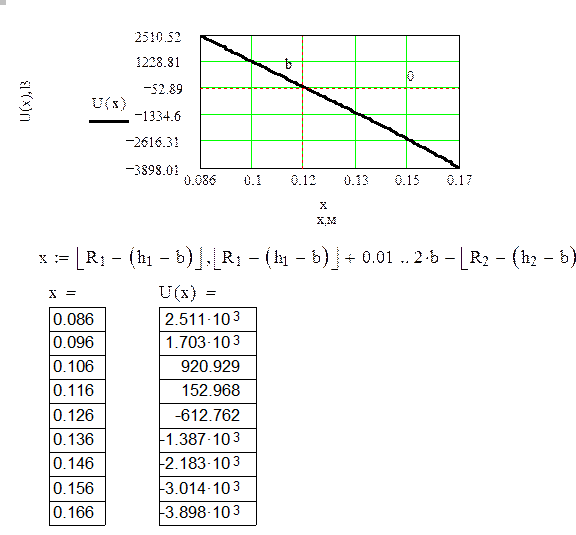
2).Изменение напряженности электростатического поля на линии, соединяющей наиболее близкие точки цилиндров:

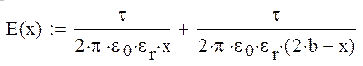
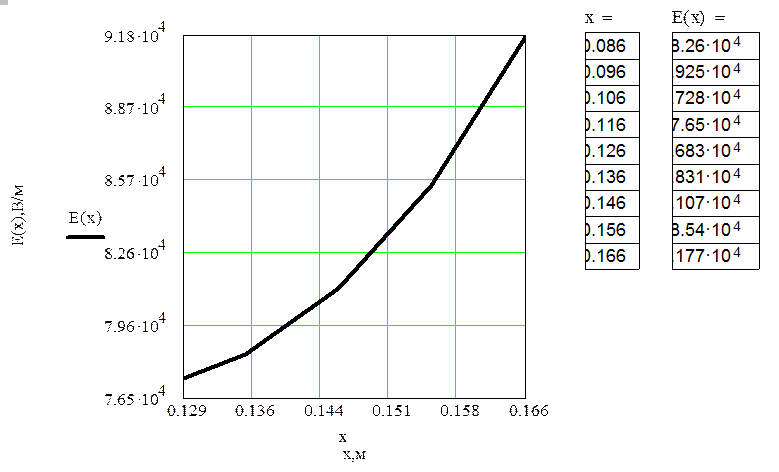 3). Распределение плотности заряда на поверхности цилиндра меньшего радиуса:

Исходя из граничных условий на поверхности раздела проводника и диэлектрика имеем:

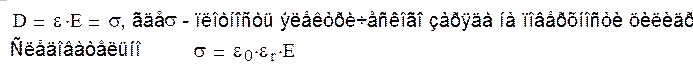
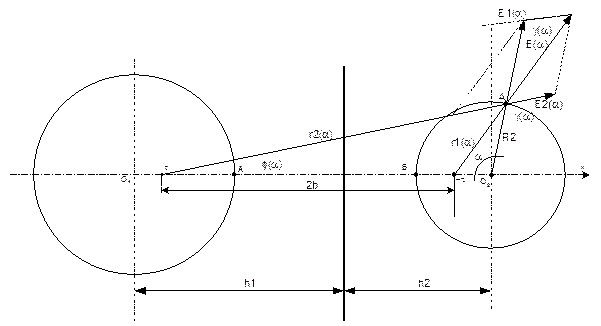
В результате некоторых геометрических соображений и принципа суперпозиции получим:

Расчет будем вести в зависимости от угла a. Рассмотрим треугольник : 

По теореме косинусов, (зная  , угол a) найдем:

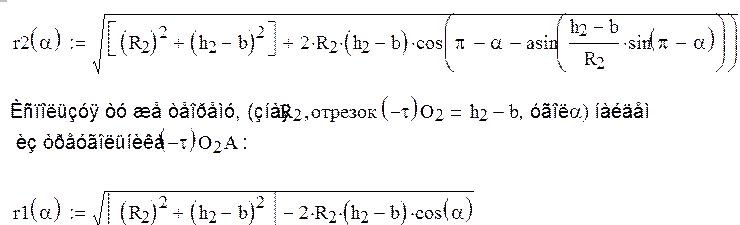
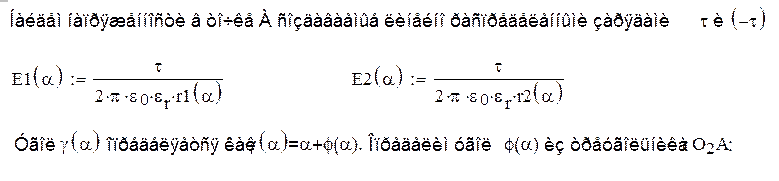
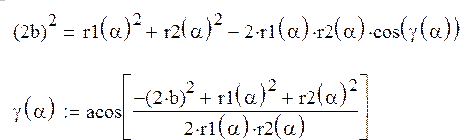
Из треугольника, создаваемого векторами , ,  (вектор  путем параллельного переноса перенесём в конец вектора  при этом угол  сохранит свою величину см. рисунок 3), зная модули векторов ,  и угол между ними, т.е.  по теореме косинусов найдём модуль вектора :