Задача №3.
Расчёт линии с распределёнными параметрами.
В соответствии с исходными данными требуется
1. Рассчитать первичные и волновые параметры линии, фазовую скорость распространения и длину волны.
2. Определить значения напряжений и токов (падающей волны, отражённой волны, полное) в следующих точках линии: x=0, x=0.5L, x=L. По результатам расчёта построить законы распределения напряжений и токов в середине линии.
3. Произвести расчёт частотной характеристики входного сопротивления линии. По результатам расчёта графически построить частотную характеристику аргумента входного сопротивления.
|
Тип линии |
Воздушная двухпроводная |
|
|
Длина линии |
L=5 км |
|
|
Расстояние между проводами |
a=600 мм |
|
|
Диаметр провода |
d=4 мм |
|
|
Материал жил и его характеристики |
Медь ρ=0.0292 Ом*мм2/м (удельное сопротивление) αR=0.0037 (температурный коэффициент сопротивления) μ=1 (магнитная проницаемость) |
|
|
Частота |
f=50 кГц |
|
|
Температура воздуха |
t=+25°С |
|
|
Состояние погоды |
Сыро |
|
|
Генератор |
Сопротивление |
кОмZgen=0.3 |
|
Фаза |
|
|
|
Нагрузка |
Сопротивление |
Zload=0.3кОм |
|
Фаза |
|
|
|
Напряжение |
U2=10 В |
|
Расчёт волновых параметров линии.
Сопротивление проводов двухпроводной линии при постоянном токе на единицу длины (R20), сопротивление единицы длины линии на постоянном токе при температуре t (Rt):
![R[20] = 8000*rho/(Pi*d^2), R[t] = R[20]*(1+alpha[R]*(t-20))](https://files3.vunivere.ru/workbase/00/03/70/22/images/image005.jpg)
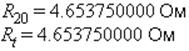
Резистивное сопротивление единицы длины линии при переменном токе (R0, где F(x) – поправочный коэффициент, учитывающий увеличение резистивного сопротивления линии вследствие поверхностного эффекта; является функцией параметра x; определяется через интерполяцию табулированной функции):
![R[0] = R[t]*(1+F(x)), x = 7.09*sqrt(1/10000*f*mu/R[t])](https://files3.vunivere.ru/workbase/00/03/70/22/images/image007.jpg)
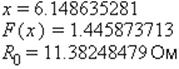
Индуктивность двухпроводной воздушной воздушной линии на единицу длины при переменном токе (L0, где r – радиус проводов, Q(x) –коэффициент, учитывающий внутреннюю индуктивность линии; является функцией параметра x; определяется через интерполяцию табулированной функции):
![]()
Ёмкость двухпроводной воздушной линии на единицу длины (C0):
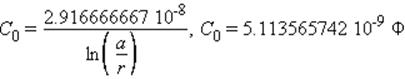
Проводимость изоляции единицы длины двухпроводной линии (G0, где G’ – проводимость изоляции при постоянном токе, равная 0.01*10-6 См/км при сухой погоде; n – коэффициент диэлектрических потерь в изоляторах, равный 0.05*10-9 при сухой погоде):
![]()
Циклическая частота протекающего через линию тока (ω):
![]()
Волновое сопративление (Zv):
![Z[v] = sqrt((R[0]+I*omega*L[0])/(G[0]+I*omega*C[0]))](https://files3.vunivere.ru/workbase/00/03/70/22/images/image013.jpg)

Километрический коэффициент (γ, α - километрический коэффициент затухания, β - километрический коэффициент фазы):
![]()

Фазовая скорость (vphase), длина волны (λ):
![v[phase] = omega/beta, lambda = 2*Pi/beta](https://files3.vunivere.ru/workbase/00/03/70/22/images/image018.jpg)

Определение напряжений и токов в заданных точках линии.
![U[2] = 10, Z[load] = abs(Z[load])*exp(I*load_phi), I[2] = U[2]/Z[load]](https://files3.vunivere.ru/workbase/00/03/70/22/images/image020.jpg) ,где
,где
Zload – комплексное сопротивление нагрузки,
I2 – ток в нагрузке.

![]() , где
, где
y - расстояние, отсчитываемое от условного конца линии.
![U[p] = 1/2*(U[2]+I[2]*Z[v])*exp(gamma*y)](https://files3.vunivere.ru/workbase/00/03/70/22/images/image023.jpg) ,
, ![U[o] = 1/2*(U[2]-I[2]*Z[v])*exp(-gamma*y)](https://files3.vunivere.ru/workbase/00/03/70/22/images/image024.jpg) , где
, где
Up – напряжение падающей волны,
Uo – напряжение отражённой волны.
![]()
![I[p] = U[p]/Z[v], I[o] = U[o]/Z[v], I = I[p]-I[o]](https://files3.vunivere.ru/workbase/00/03/70/22/images/image026.jpg)
|
X, км |
Uп(x), В |
Uо(x), В |
U(x), В |
Iп(x), А |
Iо(x), А |
I(x), А |
|
0 |
10,852ej105,707 |
0.79ej28.72 |
11,056ej101,709 |
0.0161ej106.299 |
0.00117ej29,311 |
0,0158ej110,430 |
|
|
10,73ej51,374 |
0,8ej83,052 |
11,419ej53,482 |
0,0159ej51,956 |
0,00119ej83,644 |
0,0149e49,571 |
|
|
10,611ej-2,96 |
0,81ej137.385 |
10ej0 |
0,0157ej-2,368 |
0,00120ej137,97 |
0,0167ej-5 |
Функции напряжений и токов определяются по их комплексным значениям через следующее соотношение:
F(t)=|F|sin(ωt+arg(F))
Выполним расчёт функций:

Построим графики рассчитанных функций:
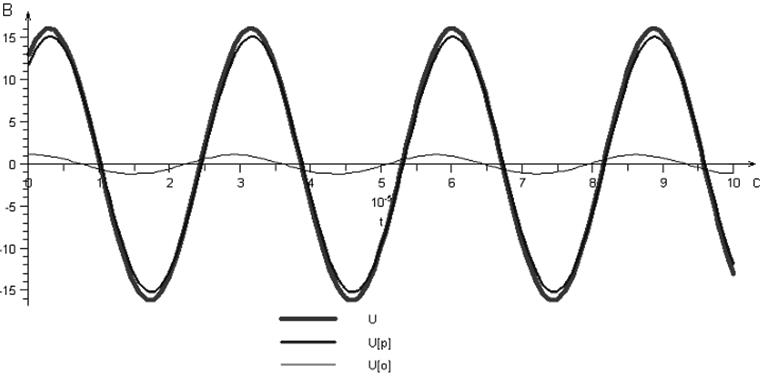
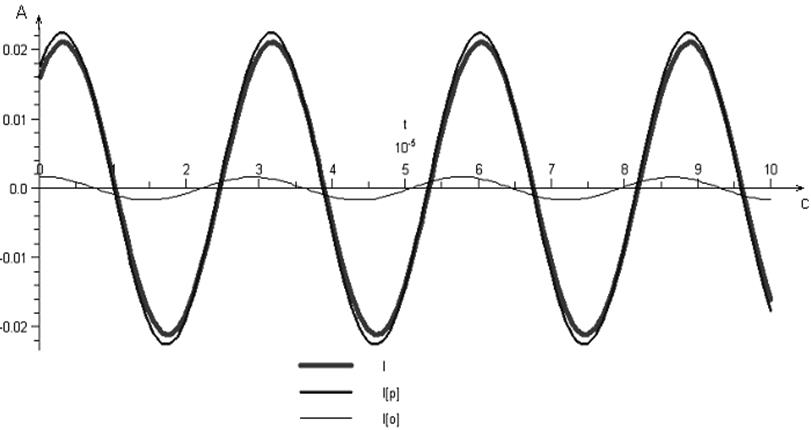
Расчёт частотной характеристики входного сопротивления линии (аргумент).
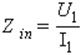 , где
, где
Zin – входное сопротивление линии,
U1 – напряжение на входе,
I1 – ток на входе (ток генератора).
![U[1] = U[2]*exp(gamma*L)*(1+K[2]*exp(-2*gamma*L))/(1+K[2])](https://files3.vunivere.ru/workbase/00/03/70/22/images/image035.jpg)
![I[1] = I[2]*exp(gamma*L)*(1-K[2]*exp(-2*gamma*L))/(1-K[2])](https://files3.vunivere.ru/workbase/00/03/70/22/images/image036.jpg)
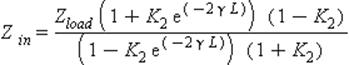 , где
, где
![K[2] = (Z[load]-Z[v])/(Z[load]+Z[v])](https://files3.vunivere.ru/workbase/00/03/70/22/images/image038.jpg)
Табулируем функцию arg(Zin):
|
f, Гц |
arg(Zin), рад |
|
3888.888889 |
0.1256553669 |
|
7777.777778 |
0.1398327167 |
|
11666.66667 |
0.1264076197 |
|
15555.55556 |
0.08902762268 |
|
19444.44444 |
0.03482025446 |
|
23333.33333 |
-0.02662886693 |
|
27222.22222 |
-0.08443418335 |
|
31111.11111 |
-0.1286748910 |
|
35000 |
-0.1522013241 |
Построим её график:
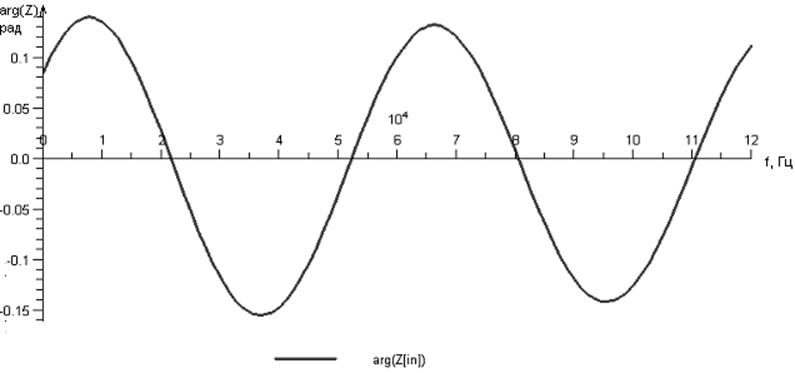
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.