Расчет энтропийных характеристик сложного сигнала

Белорусский государственный университет транспорта

Кафедра «Системы передачи информации»

ОТЧЁТ

ПО ПРАКТИЧЕСКОМУ ЗАНЯТИЮ №3

на тему:

РАСЧЁТ ЭНТРОПИЙНЫХ ХАРАКТЕРИСТИК
СЛОЖНОГО СИГНАЛА

Вариант №2

Гомель – 2004

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3

РАСЧЁТ ЭНТРОПИЙНЫХ ХАРАКТЕРИСТИК
СЛОЖНОГО СИГНАЛА

Цель работы: Рассчитать характеристики энтропии сложного сигнала, полученного объединением двух сигналов X и Y.

1.Краткие сведения из теории.

Энтропия сложного сигнала, полученного объединением двух независимых сигналов, равна сумме энтропий каждого из сигналов. Под объединением двух сигналов X и Y с возможными состояниями  понимается сложный сигнал (X,Y), состояния которого  представляет собой все возможные  комбинации состояний сигналов X и Y. Число возможных состояний сложного сигнала (X,Y) равно . Вероятность того, что сложный сигнал будет находиться в состоянии , в общем случае  равна , где  - вероятность появления сигнала ; - условная вероятность того, что сигнал Y будет находиться в состоянии  при условии, что сигнал X принял состояние .

Для независимых сигналов ; . Энтропия объединенного  сигнала (X,Y) находится по формуле

                        (1)

С учетом того, что:

;

;

из (1) следует:

.

Энтропия сложного сигнала, полученного объединением двух зависимых сигналов, равна сумме энтропий одного из сигналов и условной энтропии другого:

, где

;        (2)

.

величина называется условной энтропией сигнала Y относительно сигнала X.  - условная энтропия, это количество информации, которое содержится в сигнале , появившемся после сигнала .

Из (2) видно, что  равна математическому ожиданию величины  которая характеризует энтропию сигнала Y при условии, что сигнал находится в состоянии .

Величина  называется частной условной энтропией сигнала Y. Следовательно, условная энтропия равна среднему значению частных условных энтропий и характеризует среднюю неопределенность сигнала Y при известных состояниях сигнала X. Изложенное относится и к условной энтропии сигнала X относительно сигнала Y, т.е. . Условная энтропия также является неотрицательной величиной и изменяется в пределах , при этом нижняя граница соответствует случаю жесткой функциональной связи сигналов X и Y, а верхняя – случаю статистически независимых сигналов.

2.Методика выполнения работы.

В данной работе будут использоваться следующие формулы:

- расчёт энтропии объединенного сигнала:

;

- расчет энтропии отдельных сигналов:

;

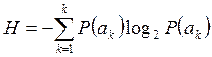- расчет вероятности:

3.Исходные данные для расчёта.

4.Результаты расчётов.

Найдем энтропию объединенного сигнала :

.

Подставляя числовые значения, получаем

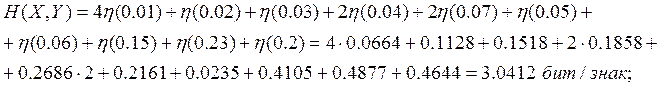Найдем вероятности и :

5.Вывод.

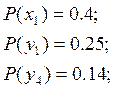
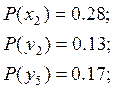
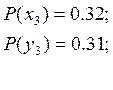
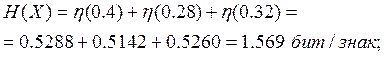
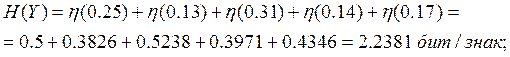
По полученным в результате расчета значениям характеристик энтропии сложного сигнала можно сделать вывод о том, что между сигналами X и Y нет жесткой функциональной связи, т.е. энтропия сложного сигнала не определяется энтропией одного из сигналов X или Y.