Расчет электрических цепей со специальными характеристиками, страница 3

x = 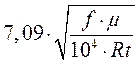 = 6,913 .

Величине x = 6,913 соответствует значение F(x), равное 1,713, тогда:

Ro = 12,841 Ом / км .

Индуктивность двухпроводной воздушной линии на единицу длины при переменном токе определим по формуле:

Lo =,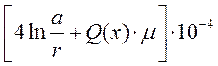

где r – радиус проводов,

      Q(x) – коэффициент, учитывающий внутреннюю индуктивность линии, Q(x) = 0,406.

Lo = 2,322 Гн / км .

Ёмкость двухпроводной воздушной линии на единицу длины:

Co = 1,05 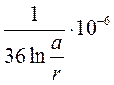^.  = 5,114Ф / км,

где коэффициент 1,05 учитывает влияние изоляторов и соседних проводов на ёмкость линии.

Проводимость изоляции единицы длины двухпроводной линии:

Go = G’+nf,

где G’ – проводимость изоляции при постоянном токе (0,5 См / км при сырой погоде),

       n – коэффициент диэлектрических потерь в изоляторах, равный 0,25 при сырой погоде.

Go = 1,175 См / км .

Волновое сопротивление определим по формуле

Zв = ,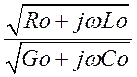

Zв = 673, 918 – j3,815 = 673,929Ом

Коэффициент распространения:

γ =,

γ = 0,013 + j0,974 км.

Рабочая постоянная передачи определяется из соотношений:

gраб = aраб + jbраб,

где         aраб = Re(g)l       и        bраб = Im(g)l.

Построим графики зависимости рабочего затухания и рабочего коэффициента фазы от частоты.

Зависимость рабочего затухания от частоты:

 

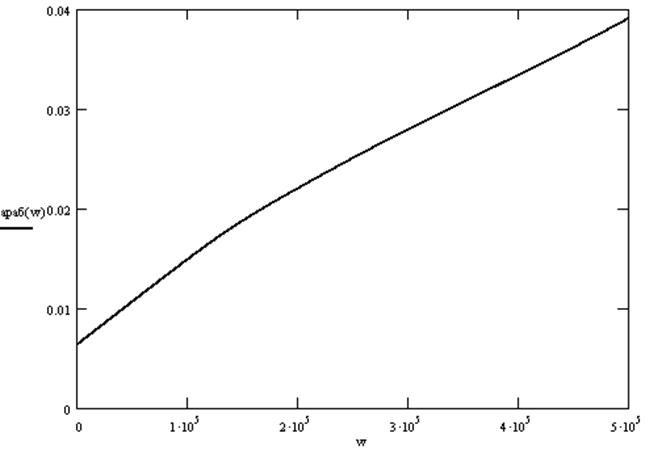Зависимость рабочего коэффициента фазы от частоты:

 

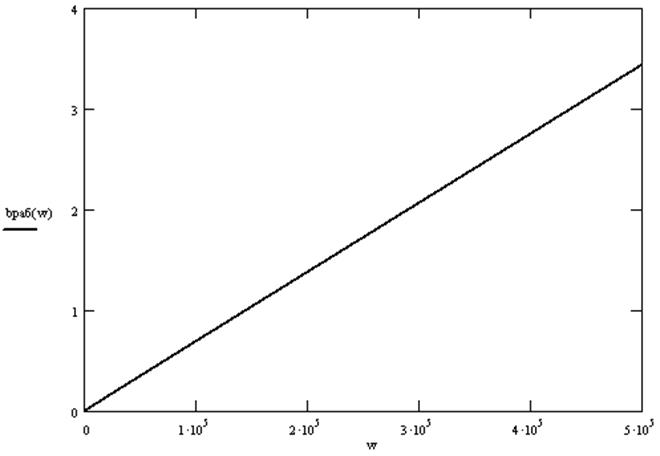Так как фазочастотная характеристика линии представляет собой линейную зависимость, то произведем лишь расчет АВК.

Так как по заданию минимальное затухание АВК на верхней частоте заданного диапазона должно составлять 5% от рабочего затухания линии на этой частоте, то найдём его:

а_к(w_верх) = 0.05 ^. a_раб(1.2 ^. 2p ^. f_раб),

где w_верх = 1.2 ^. 2p ^. f_раб – верхняя частота заданного диапазона,

       a_раб(1.2 ^. 2p ^. f_раб) = 0.03 – затухание линии на этой частоте.

а_к(w_верх) = 1.506 ^. 10^-3 Нп

Построим частотную характеристику затухания АВК:

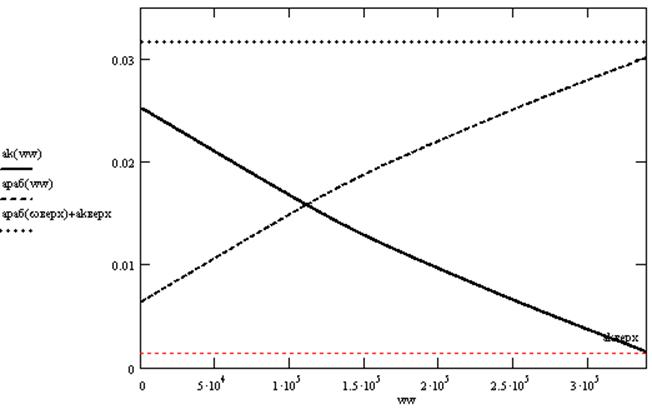
На графике ak(w) – частотная характеристика АВК, a_раб(w) – частотная характеристика линии, a_раб(w_верх) – требуемая характеристика затухания. Тонкой линией снизу отмечено значение а_к(w_верх).

2. Выберем схему АВК и выведем уравнение затухания контура.

Выберем АВК первого порядка. Схема – «перекрещенное Т».

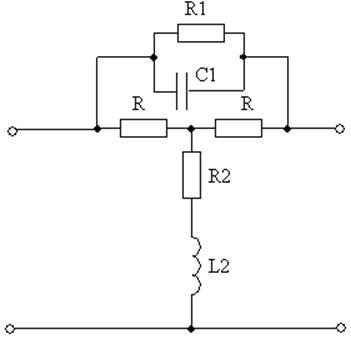
Выведем уравнение затухания контура.

Общее уоавнение затухания АВК:

,

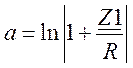где ,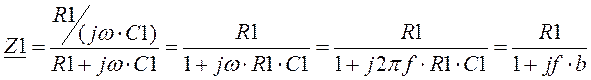

где b = 2p ^. R1 ^. C1.

,

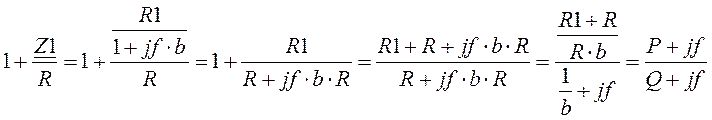где , .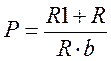

Таким образом получаем:

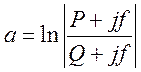
или

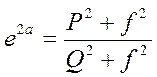
Обозначим последнюю величину как F. Тогда уравнение АВК 1-го порядка имеет вид:

.

3. Рассчитаем параметры элементов контура.

Пусть f = f1 = 0.1 ^. f_раб, тогда ak1 = ak(2pf1) = 0.023 Нп, F1 = = 1.047.

Пусть f = f2 = 1.2 ^. f_раб, тогда ak2 = ak(2pf2) = 1.506 ^. 10^-3 Нп, F2 = = =1.003.

Значения P и Q получим, решая следующую систему:

 

   

   

Полученные значения P и Q:

P = 13750.229, Q = 13406.450.

Теперь найдем параметры элементов, используя следующие формулы:

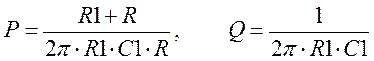
Приняв R равным |Zн|, находим параметры элементов:

R1 = 28.207 Ом,    С1 = 0.421 ^. 10^-6 Ф.

Зная R, R1 и C1, получим параметры элементов R2 и L2:

R2 = R²/R1 = 42896.999 Ом,        L2 = R^{2 .} C1 = 0.509 Гн.

4. Произведем проверочный расчет, учитывая что расчетные характеристики не должны отличаться от требуемых более чем на 10%.

Как мы помним:  Z1(w) = ,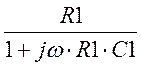

Расчетная характеристика затухания akрас(w) = .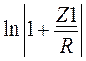

Полученная расчетная характеристика затухания представлена на следующем рисунке.

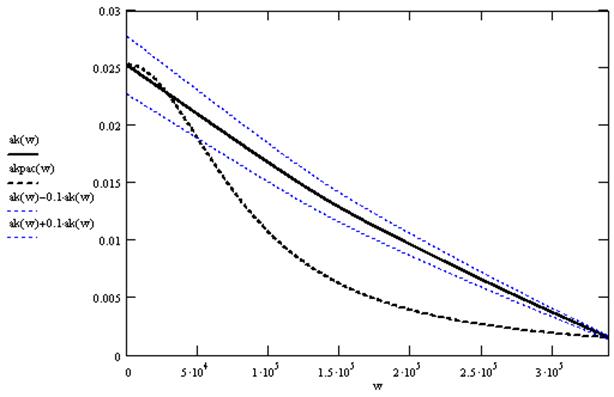
Здесь ak(w) – требуемая характеристика, ak_рас(w) –расчетная характеристика. Тонкими линиями обозначена граница 10%, в пределах которой должна находиться расчетная характеристика.