Теория дискретных устройств (ТДУ) является сравнительно молодой и быстро развивающейся отраслью науки. Её появление в 30 – х годах нашего столетия связано с усложнением и совершенствованием релейных систем управления, когда возникла необходимость в их математическом описании. Новый стимул развития ТДУ получила в 50 – х годах в связи с применением в устройствах управления полупроводниковой техники и вычислительных машин. В настоящее время разрабатываются вопросы теории, связанные с использованием микросхем большой степени интеграции, программируемых логических матриц, микропроцессоров и других достижений современной микроэлектроники.
Основы ТДУ начали закладываться в 1938 – 1940 гг., когда советский физик В.И.Шестаков, американский математик К.Шеннон и японский учёный А.Накашима доказали возможность использования булевой алгебры при анализе и синтезе контактных схем. Впервые же указал на такую возможность в 1910 г. русский физик П.Эрнефест.
Большое влияние на развитие ТДУ оказало создание электронных вычислительных машин (ЭВМ). Крупный вклад в указанную теорию и практику дискретной техники, особенно в применении к ЭВМ, внёс академик В.М.Глушков.
Устройства железнодорожной автоматики, телемеханики и связи в основном относятся к классу дискретных устройств. К железнодорожным системам автоматики, телемеханики и связи предъявляют повышенные требования с точки зрения надёжности, безопасности и устойчивости работы. [1. – cc.5-6]
1.1 Генератор прямоугольных импульсов
Генератор прямоугольных импульсов (рисунок 1) собран на логических элементах И-НЕ.
В данной схеме резистор R1 используется для начального запуска генератора. Напряжение на выходе генератора имеет вид последовательности прямоугольных импульсов, которые в свою очередь воздействуют на другие составляющие части дискретного устройства.
Частота генерации задается с высокой точностью с помощью кварцевого резонатора ZQ1.
Для стабилизации взят кварцевый резонатор на 100000 кГц РПК01.
В соответствии с выходной частотой возьмём R1 = 1 кОм.
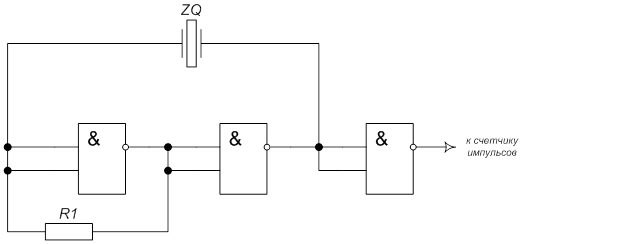
Рисунок 1.1 – Схема генератора прямоугольных импульсов
 |
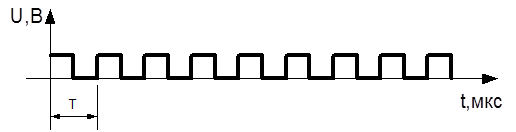Рисунок 1.2-Временная диаграмма работы генератора прямоугольных импульсов.
Исходя
из того, что частота кварцевого резонатора 100000 кГц, период импульсов будет
равен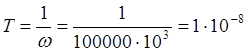 
с = 0.01 мкс
Синтез счётчика.
Счётчиком называют устройство, на выходе которого сигналы в определённом коде отображают число импульсов, поступивших на счётный вход (пришедших с генератора импульсов). По заданию необходимо разработать паралельный, вычитающий счетчик с коэффициентом счета 19. В качестве устройств памяти необходимо использовать JK- триггеры. Вид выходного кода 2 из 5.
Для разработки данного счетчика составим таблицу. Данные таблицы имеют следующий вид: в первом столбце записан номер состояния выходов, во втором столбце - текущее состояние выходов счетчика до подачи на вход тактового импульса, в третьем столбце - последующее состояние выходов счетчика после подачи на его вход тактирующего импульса, в четвертом столбце - состояния на информационных входах JK–триггеров, которые должны быть на JK-входах триггеров, чтобы с приходом тактирующего импульса триггеры переключились в следующее состояние. Реализуем данный алгоритм работы счетчика на логических элементах И - НЕ.
Для минимизации функций информационных воздействий на входы триггеров воспользуемся методом карт Карно.
Таблица 1 - Таблица состояний.
|
№ |
Текущее состояние |
Последующее состояние |
Сигналы на информационных входах JK-триггеров. |
|||||||||||||||||
|
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
J1 |
K1 |
J2 |
K2 |
J3 |
K3 |
J4 |
K4 |
J5 |
K5 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
- |
0 |
0 |
- |
- |
0 |
0 |
- |
- |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
- |
0 |
0 |
- |
- |
1 |
1 |
- |
1 |
- |
|
2 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
- |
0 |
0 |
- |
0 |
- |
- |
0 |
- |
1 |
|
3 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
- |
0 |
0 |
- |
0 |
- |
- |
1 |
1 |
- |
|
4 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
- |
0 |
0 |
- |
0 |
- |
0 |
- |
- |
1 |
|
5 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
- |
1 |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
|
6 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
- |
- |
0 |
- |
0 |
- |
0 |
- |
1 |
|
7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
- |
- |
0 |
- |
0 |
- |
1 |
1 |
- |
|
8 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
- |
- |
0 |
- |
0 |
0 |
- |
- |
1 |
|
9 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
- |
- |
0 |
- |
1 |
1 |
- |
1 |
- |
|
10 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
- |
- |
0 |
0 |
- |
- |
0 |
- |
1 |
|
11 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
- |
- |
0 |
0 |
- |
- |
1 |
1 |
- |
|
12 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
- |
- |
0 |
0 |
- |
0 |
- |
- |
1 |
|
13 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
- |
- |
1 |
1 |
- |
1 |
- |
1 |
- |
|
14 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
- |
0 |
- |
- |
0 |
- |
0 |
- |
1 |
|
15 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
- |
0 |
- |
- |
0 |
- |
1 |
1 |
- |
|
16 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
- |
0 |
- |
- |
0 |
0 |
- |
- |
1 |
|
17 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
- |
0 |
- |
- |
1 |
1 |
- |
1 |
- |
|
18 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
- |
0 |
- |
0 |
- |
- |
0 |
- |
1 |
|
19 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
- |
0 |
- |
0 |
- |
- |
1 |
1 |
- |
|
20 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
- |
1 |
|
21 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
- |
0 |
- |
1 |
- |
0 |
- |
1 |
- |
Таблица 2 - Таблица переходов триггера.
|
Тип перехода |
Вход J |
Вход K |
|
0®0 |
0 |
~ |
|
0®1 |
1 |
~ |
|
1®0 |
~ |
1 |
|
1®1 |
~ |
0 |
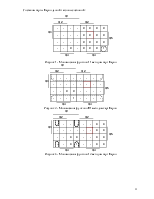
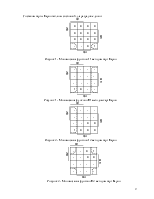
Составим карты Карно данной таблицы состояний:
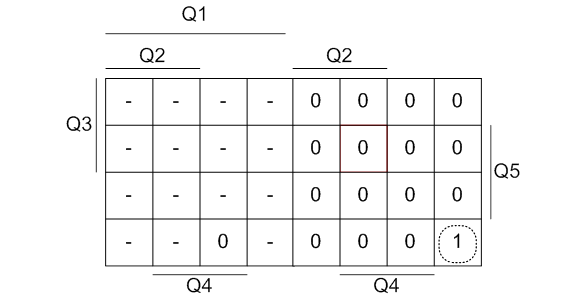
Рисунок 1 - Минимизация функции J1 методом карт Карно
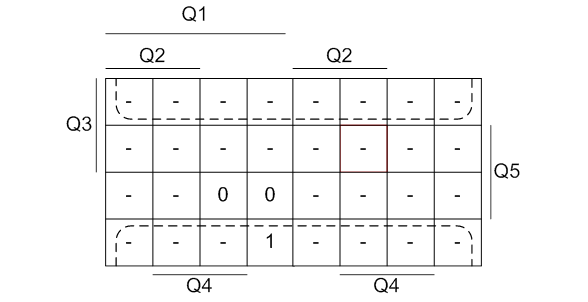
Рисунок 2 - Минимизация функции K1 методом карт Карно
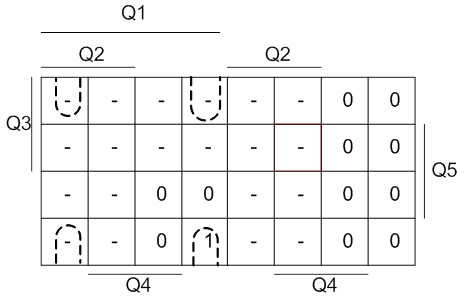
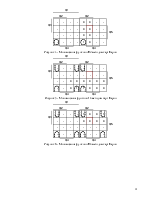
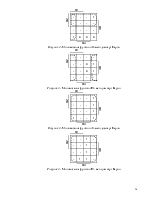
Рисунок 3 - Минимизация функции J2 методом карт Карно
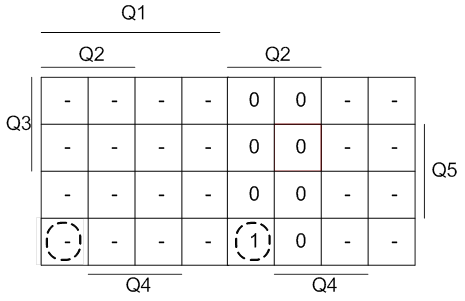
Рисунок 4 - Минимизация функции K2 методом карт Карно
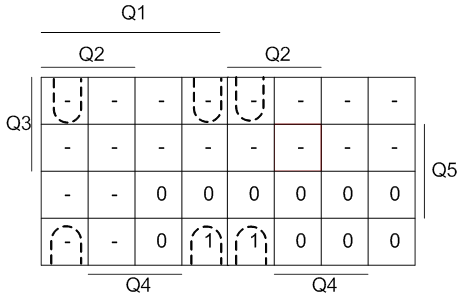
Рисунок 5 - Минимизация функции J3 методом карт Карно
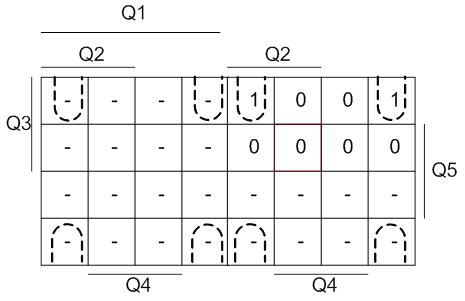
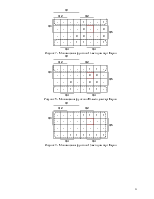
Рисунок 6 - Минимизация функции K3 методом карт Карно
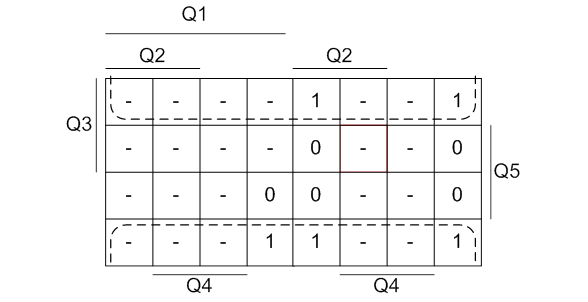
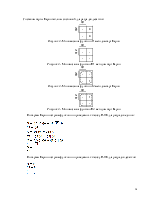
Рисунок 7 - Минимизация функции J4 методом карт Карно
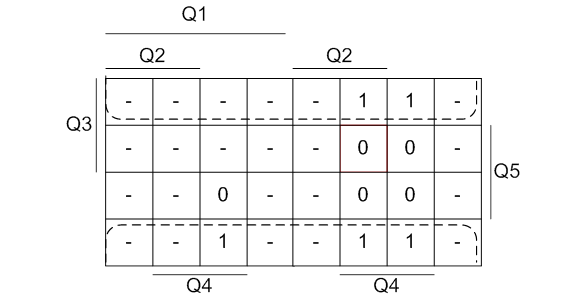
Рисунок 8 - Минимизация функции K4 методом карт Карно
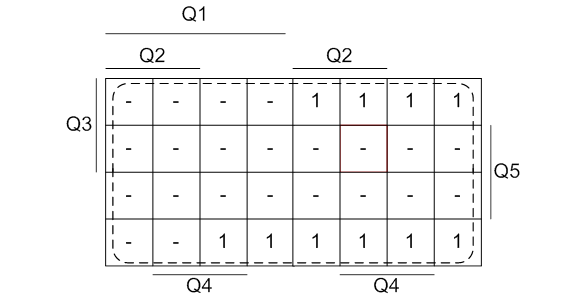
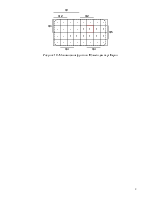
Рисунок 9 - Минимизация функции J5 методом карт Карно
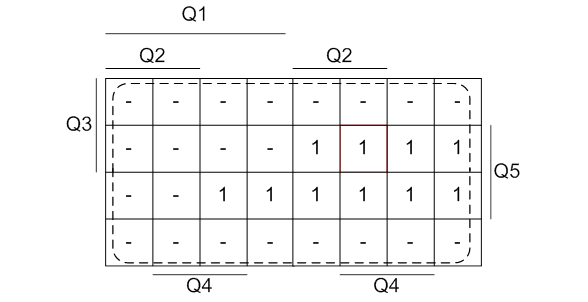
Рисунок 10 - Минимизация функции K5 методом карт Карно
По картам Карно построим функции и приведём их к базису И-НЕ:
По полученным функциям построим счётчик.
Синтез счётчика.
По заданию необходимо разработать последовательно-паралельный, вычитающий счетчик с коэффициентом счета 19. В качестве устройств памяти необходимо использовать JK- триггеры. Вид выходного кода 2 из 5.
Для разработки данного счетчика составим таблицу. Данные таблицы имеют следующий вид: в первом столбце записан номер состояния выходов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.