








Примеры решения алгебро-дифференциальных уравнений в СКМ Maple
Рассмотрим простейший пример из двух уравнений, одно из которых дифференциальное, а другое - алгебраическое.
Найдём решение, не задавая начальных условий:
> restart:
> Du := diff (x(t),t) + 2*y(t) = 2, 5*x(t) + y(t) = 2*sin(3*t) :
> Ds := { x(t) , y(t) }:
> Rs := dsolve ( {Du} , Ds ) :
> assign (Rs) :
> x(t) ;
![]()
> y(t) ;
![]()
Таким образом, пакет выдал решение решение с одной постоянной интегрирования.
Теперь попробуем получить решение с начальными условиями:
> restart:
> Du := diff (x(t),t) + 2*y(t) = 2, 5*x(t) + y(t) = 2*sin(3*t) :
> Nu := x(0) = 1 , y(0) = 1 :
> Ds := { x(t) , y(t) }:
> Rs := dsolve ( {Du, Nu} , Ds ) ;
![]()
Как видим, СКМ Maple выдала т.н. "нулевое" решение, т.е. аналитическое решение для системы алгебро-дифференциальной уравнений с начальными условиями в силу каких-то причин не найдено.
Следует иметь ввиду, что некоторые версии Maple не решают аналитическиалгебро-дифференциальной уравнения и системы таких уравнений, а также системы ДУ, в которых присутствует кусочно-определённые функции.
Поэтому попытаемся найти численное решение данной системы.
Для поиска численного решения системы уравнений в опциях функции dsolve необходимо указать такую : type= numeric.
Помимо этого, в опциях можно указывать метод решения. По «умолчанию» как правило пакет использует метод Рунге-Кутта порядка 4.5.
Итогом решения системы уравнений является сформированная пакетом процедура, записанная в переменную, в которую помещается решение (в нашем примере - Rs ), обратившись к которой которой можно получить решение в указанной точке либо построить график. Ниже приведены соответствующие примеры:
> restart:
> Du := diff (x(t),t) + 2*y(t) = 2, 5*x(t) + y(t) = 2*sin(3*t) :
> Nu := x(0) = 1 , y(0) = 1 :
> Ds := { x(t) , y(t) }:
> Rs := dsolve ( {Du, Nu} , Ds, type= numeric ) ;
Warning, Initial value of y(t) changed from 1.000000 to -5.000000
![]()
Ниже показано, как можно получить значения функций x(t) и y(t) в точке 0.5:
> Rs(0.5);
![]()
Теперь построим графики функций на интервале изменения аргумента от 0 до 0.1, для чего предварительно необходимо подключить пакет plots:
> with (plots):
Warning, the name changecoords has been redefined
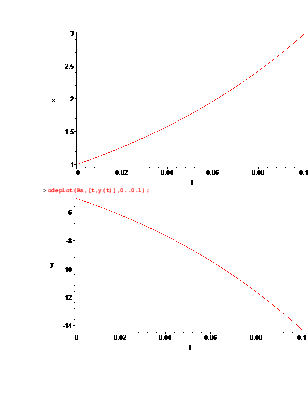
> odeplot(Rs,[t,x(t)],0..0.1);
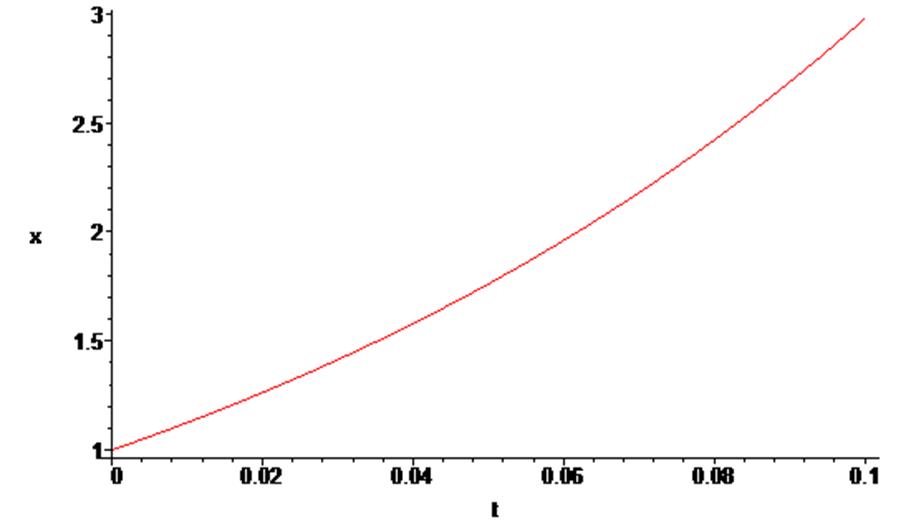
> odeplot(Rs,[t,y(t)],0..0.1);
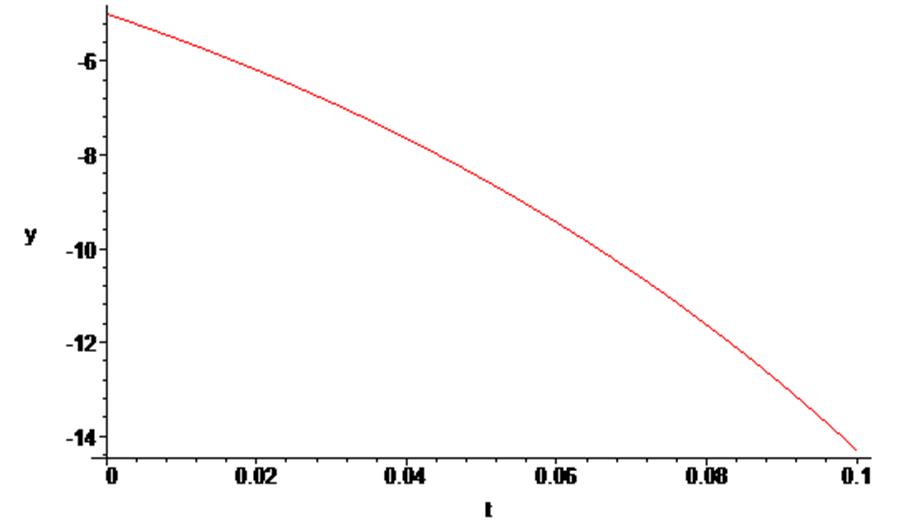
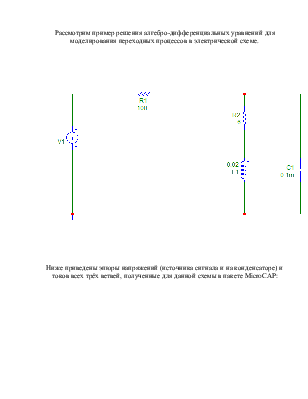
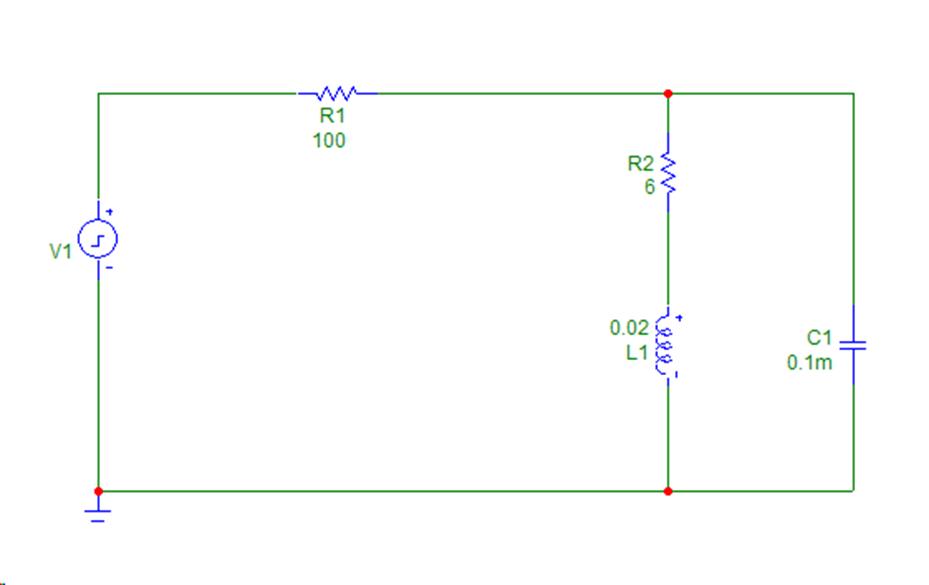
Рассмотрим пример решения алгебро-дифференциальных уравнений для моделирования переходных процессов в электрической схеме.
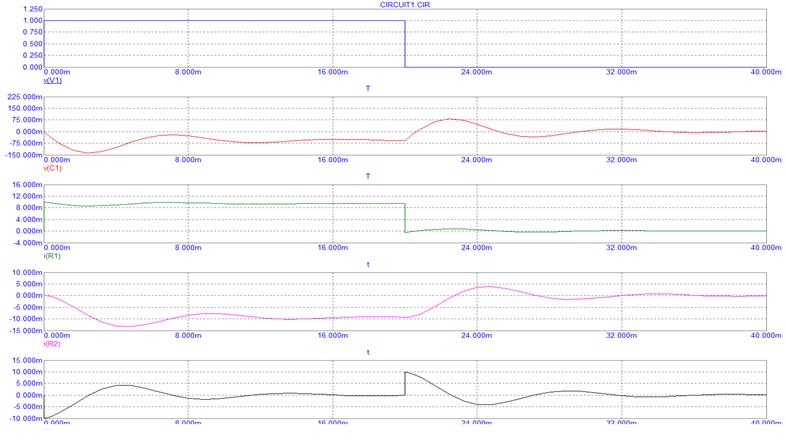
Ниже приведены эпюры напряжений (источника сигнала и на конденсаторе) и токов всех трёх ветвей, полученные для данной схемы в пакете MicroCAP:
Зададим модель в виде системы алгебро-дифференциальных уравнений (система уравнений получена по законам Кирхгофа)
и получим решение системы уравнений в СКМ Maple:
> restart:
> Du := i1(t) + i2(t) + i3(t) =0, R1*i1(t) + R2*i2(t) + L*diff (i2(t) , t) = U(t), R1*i1(t) + Uc(t) =U(t), C*diff (Uc(t),t) = i3(t) :
> R1 := 100: R2 := 6: C := 0.0001: L := 0.02:
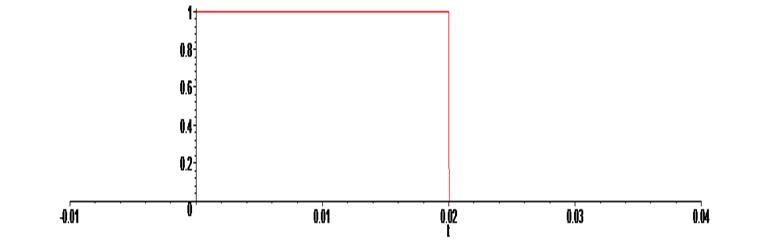
Входной сигнал U(t) зададим в виде прямоугольного импульса:
> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.02, 1, t > 0 , 0):
> plot ( U(t) , t = -0.01 .. 0.04) ;
Начальные условия зададим нулевые:
> Nu := i1(0) = 0, i2(0) = 0, i3(0) = 0, Uc(0) = 0:
> Rd := i1(t), i2(t), i3(t), Uc(t) :
> Rs := dsolve ( {Du , Nu} , {Rd} , type = numeric) ;
Warning, Initial value of i1(t) changed from 0.000000 to 0.010000
Warning, Initial value of i3(t) changed from 0.000000 to -0.010000
![]()
> Rs(0.1);
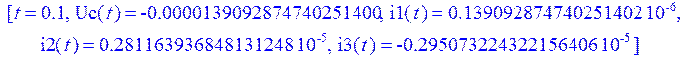
Построим графики изменения токов в ветвях цепи и напряжения на конденсаторе, воспользовавшись функцией odeplot :
> with (plots):
Warning, the name changecoords has been redefined
> odeplot(Rs,[t,i1(t)],0..0.04);
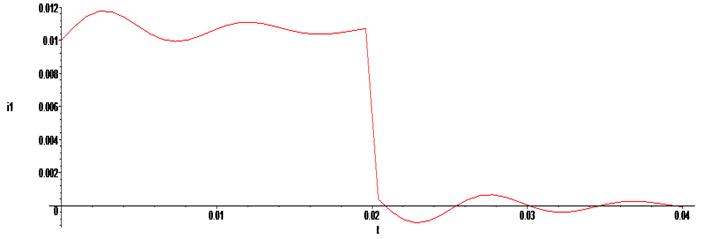
> odeplot(Rs,[t,i2(t)],0..0.04);
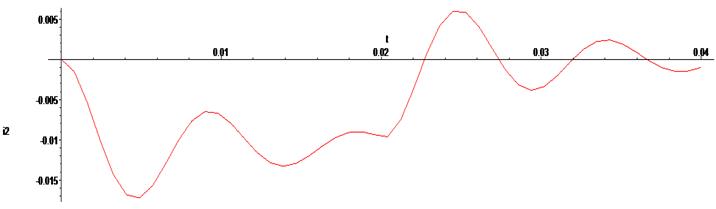
> odeplot(Rs,[t,i3(t)],0..0.04);
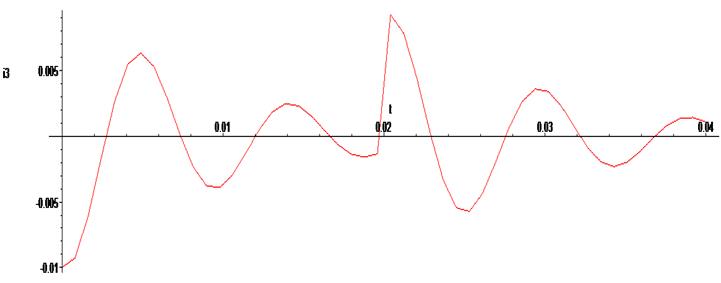
> odeplot(Rs,[t,Uc(t)],0..0.04);
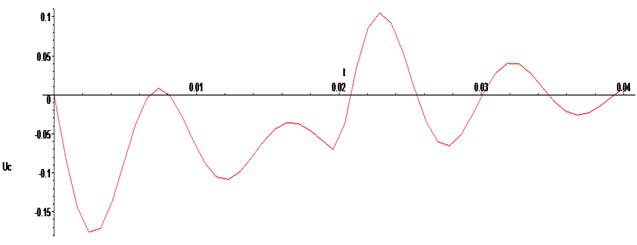
Число точек при выводе графика не большое, поэтому графики получаются при подобном их построении "ломаными". Улучшить качество их воспроизведения можно, добавив число точек кривой в опции numpoints. Приведём пример её использования, повторив вывод графики изменения напряжения на конденсаторе.
> odeplot(Rs,[t,Uc(t)],0..0.04 , numpoints = 500);
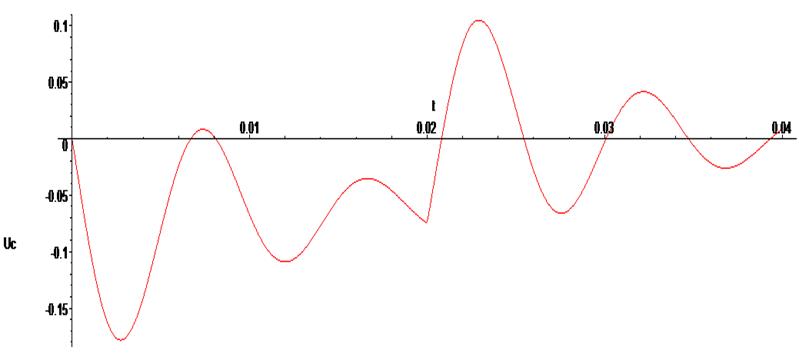
Получим решение системы при входном синусоидальном сигнале и ненулевых начальных условиях:
>
> restart:
> Du := i1(t) + i2(t) + i3(t) =0, R1*i1(t) + R2*i2(t) + L*diff (i2(t) , t) = U(t), R1*i1(t) + Uc(t) =U(t), C*diff (Uc(t),t) = i3(t) :
> R1 := 100: R2 := 6: C := 0.0001: L := 0.02:
Зададим входной синусоидальный сигнал и построим его график:
> U := (t) -> 2 * sin ( 50*Pi*t + phi ) ;
![]()
> phi := 0.01 * Pi:
> plot ( U(t) , t = 0 .. 0.03 * Pi) ;
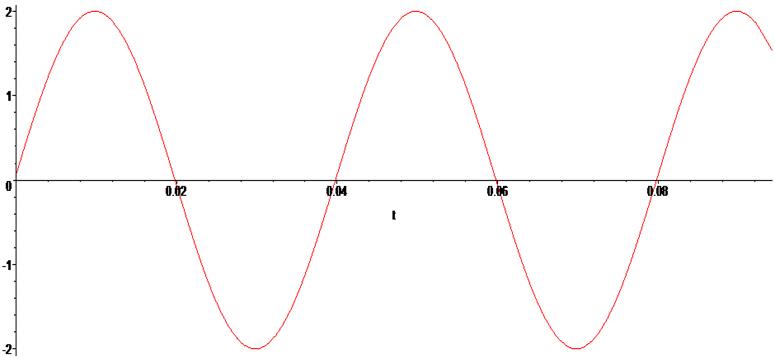
Зададим начальные условия и получим численное решение системы алгебро-дифференциальных уравнений:
> Nu := i1(0) = 0, i2(0) = 0.01, i3(0) = 0, Uc(0) = 0:
> Rd := i1(t), i2(t), i3(t), Uc(t) :
> Rs := dsolve ( {Du , Nu} , {Rd} , type = numeric) ;
Warning, Initial value of i1(t) changed from 0.000000 to 0.000628
Warning, Initial value of i3(t) changed from 0.000000 to -0.010628
![]()
> Rs(0.1); # Решение в точке t = 0.1
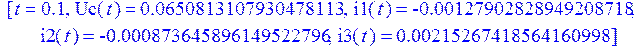
Построим графики изменения токов в ветвях цепи и напряжения на конденсаторе:
> with (plots):
Warning, the name changecoords has been redefined
> odeplot(Rs,[t,i1(t)], 0..0.03*Pi , numpoints=500);
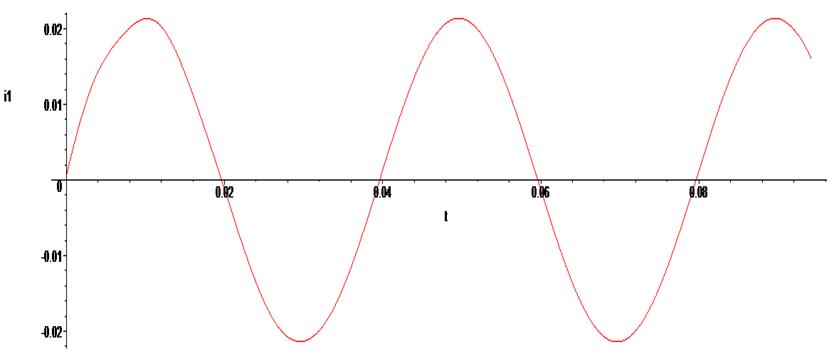
> odeplot(Rs,[t,i2(t)], 0..0.03*Pi , numpoints=500);
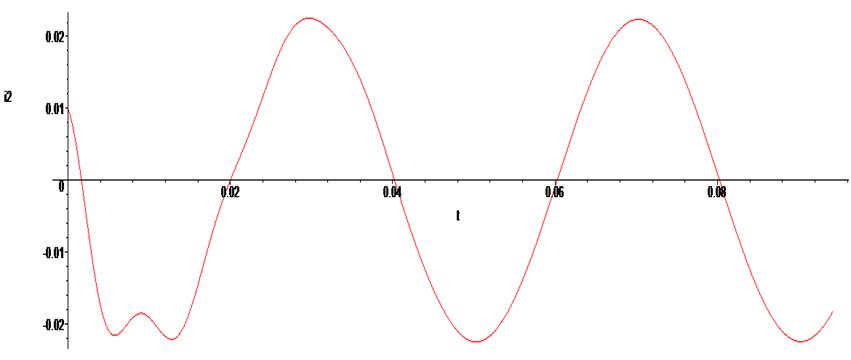
> odeplot(Rs,[t,i3(t)], 0..0.03*Pi , numpoints=500);
> odeplot(Rs,[t,Uc(t)], 0..0.03*Pi , numpoints=500);
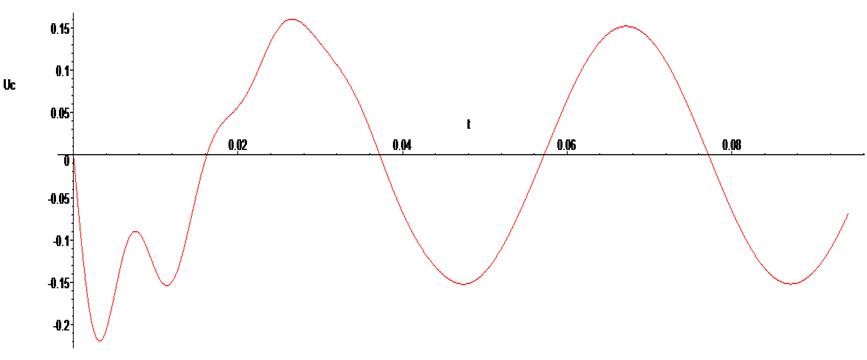
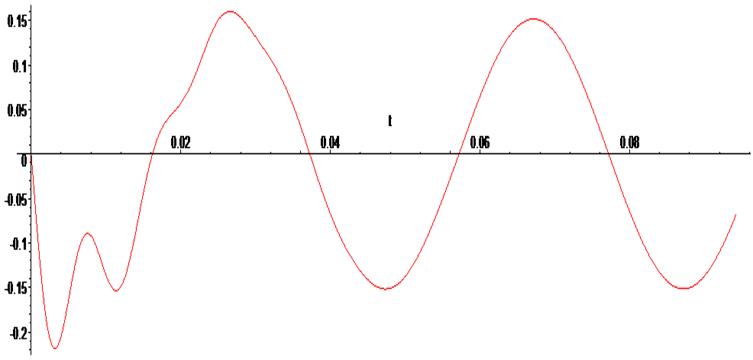
Как и следовало ожидать, в силу входного синусоидального сигнала после переходного процесса все фазовые переменные схемы переходят в режим гармонических колебаний.
Зададим модель для вышеприведённой схемы, исключив одно дифференциальное уравнение и сравним результаты решения:
> Ode := i1(t) + i2(t) + i3(t) =0, R1*i1(t) + R2*i2(t) + L*diff (i2(t) , t) = U(t), R1*diff(i1(t),t) + i3(t)/C = diff (U(t) , t ) :
> Nu1 := i1(0) = 0, i2(0) = 0.01, i3(0) = 0 :
> Rd1 := i1(t), i2(t), i3(t):
> Rs1 := dsolve ( {Ode, Nu1 } , {Rd1} , type = numeric) ;
Warning, Initial value of i3(t) changed from 0.000000 to -0.010000
![]()
> with (plots):
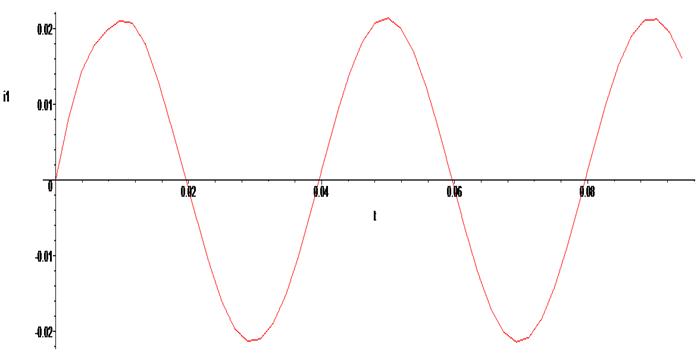
> odeplot(Rs1,[t,i1(t)],0..0.03 * Pi);
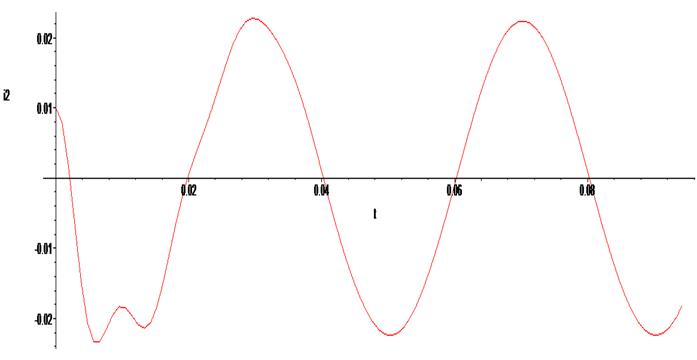
> odeplot(Rs1,[t,i2(t)],0..0.03 * Pi, numpoints = 100);
> odeplot(Rs1,[t,i3(t)],0..0.03 * Pi, numpoints = 500);
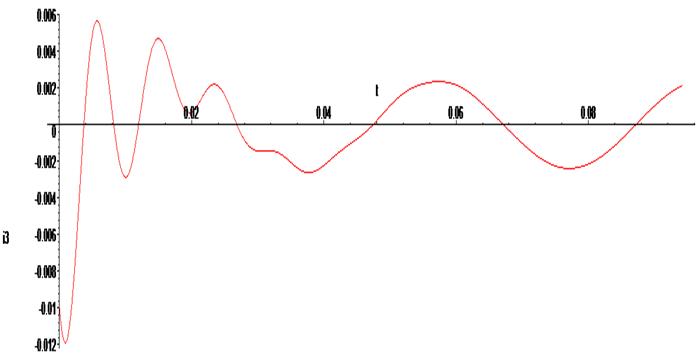
Ниже приведён график предыдущего решения. Как видим, решения идентичны. Однако, сократив систему уравнений, мы получили только графики изменений токов в ветвях цепи. Напряжение на конденсаторе необходимо находить дополнительно.
> odeplot(Rs,[t,i3(t)],0..0.03 * Pi, numpoints = 500);
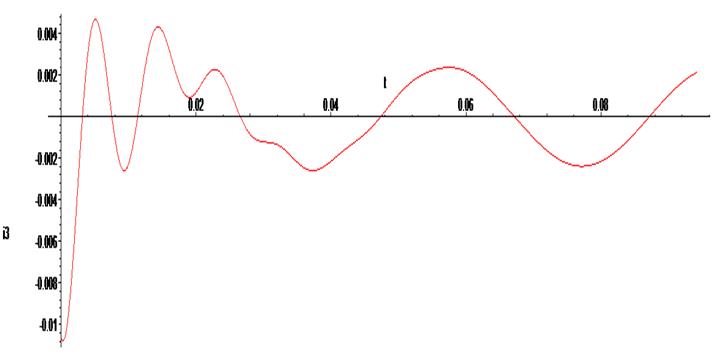
Сократив систему уравнений, мы получили только графики изменений токов в ветвях цепи. Напряжение на конденсаторе необходимо находить дополнительно. Для рассматриваемой схемы напряжение на конденсаторе можно найти как разницу между значением входного сигнала и падением напряжения на резисторе R1:
> odeplot(Rs,[ t, U(t) - i1(t)* R1 ],0..0.03 * Pi, numpoints = 500);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.