Построение дискретного устройства, имеющего заданную структурную схему

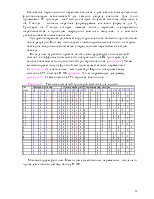
Минимизируем функцию J2 методом существенных переменных, после чего приведем к необходимому базису И-НЕ.

Таблица 3 - Таблица существенных переменных для J2

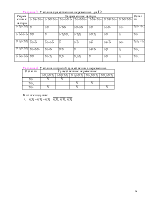
Таблица 4 - Таблица покрытий существенных переменных

В итоге получим:

;                             

;                            

;                                         

;                                                        

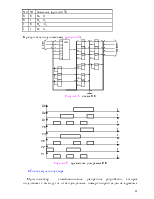
Рисунок 6 – Схема счетчика

Рисунок 7 –Временная диаграмма счетчика

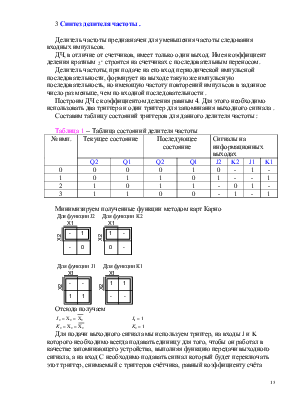
5 Синтез преобразователя кодов

Преобразователем кодов  -- комбинационное дискретное устройство, предназначенное для перевода одного двоичного кода в другой двоичный код.

Существует два метода синтеза преобразователей кодов: с использованием одной таблицы истинности и свойства независимости входов и выходов и путем последовательного включения дешифратора и шифратора.

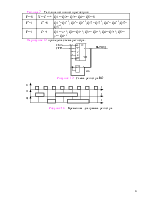
В нашем случае будем использовать первый метод синтеза. По заданию требуется построить ПК для перевода кода 8421 в код 3а+2. для этого составим таблицу истинности.

Таблица 5 - Таблица истинности

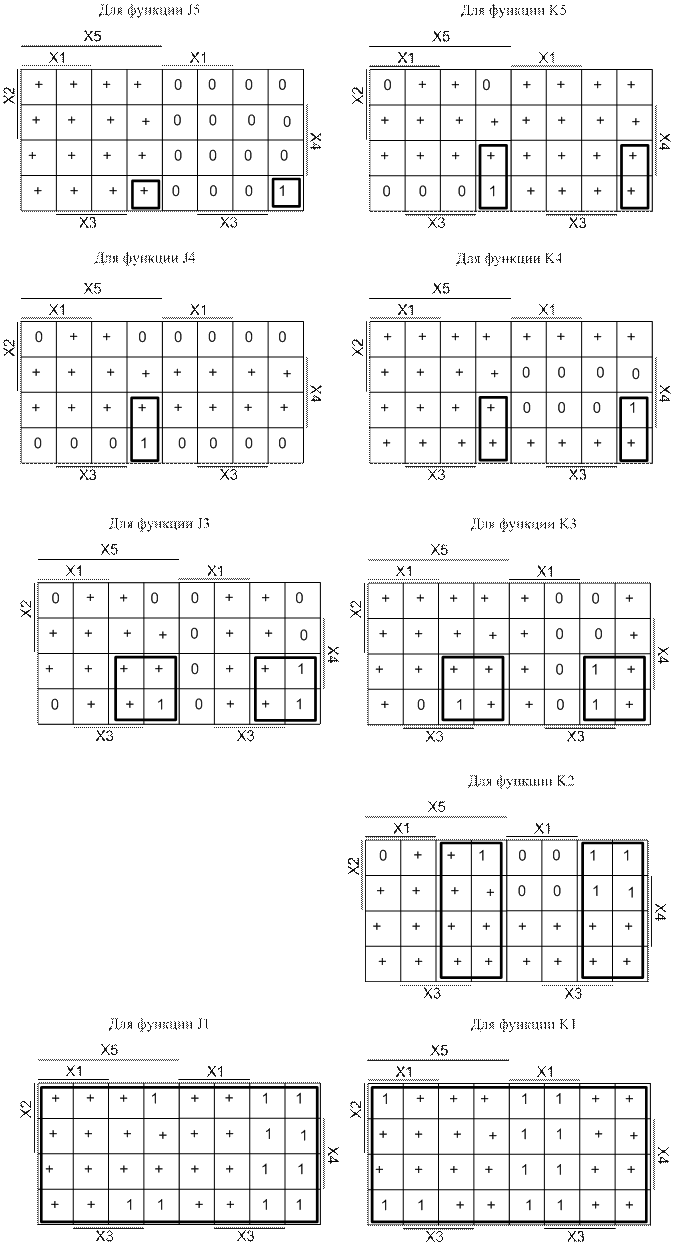
Далее для каждой функции произведем минимизацию методом Карт Карно и приведем их к базису И-НЕ:

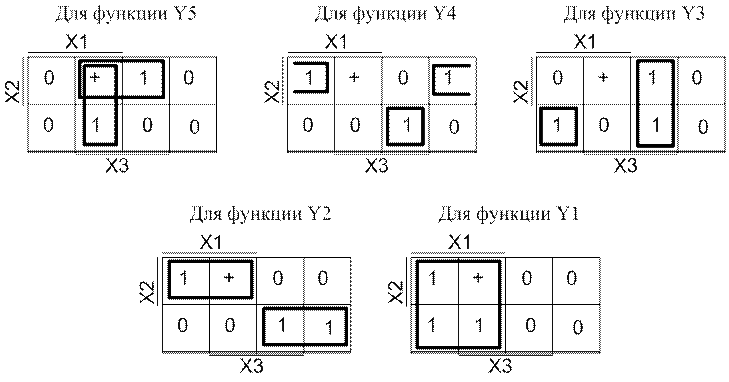
Отсюда получаем функции

Разработаем ПК, реализованный на базе асинхронных мультиплексоров (для функции Y5).

Разложим полученные функции по переменных Х1 и Х2 предварительно

составив таблицу разложения функций по этим переменным.

В результате получим схему (рисунок 8).

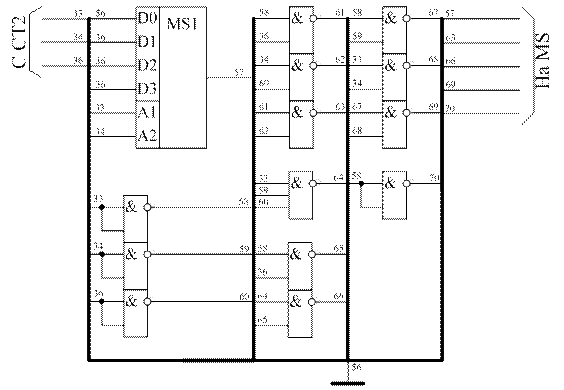
Рисунок 8 - схема ПК

Рисунок 9 - временная диаграмма ПК

6 Cинтез мультиплексора

Мультиплексор – комбинационное дискретное устройство, которое подключает к выходу тот из входов данных, номер которого задан на адресных входах при наличии сигнала синхронизации.

Построим асинхронный мультиплексор с шестью входами данных, в качестве которых служат выходы с шифратора и один разряд счетчика (Т4), и тремя адресными входами, т. е. триггеры счетчика Т1, Т2, Т3. Для  этого необходимо составить таблицу истинности (таблица 6), на основании которой запишем логическое выражение для выхода Q,  и построим схему мультиплексора в базисе И-НЕ (рисунок 10).

Таблица 6 - таблица истинности мультиплексора

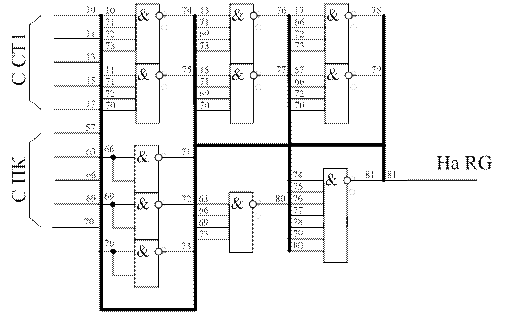
Рисунок 10 - Схема мультиплексора

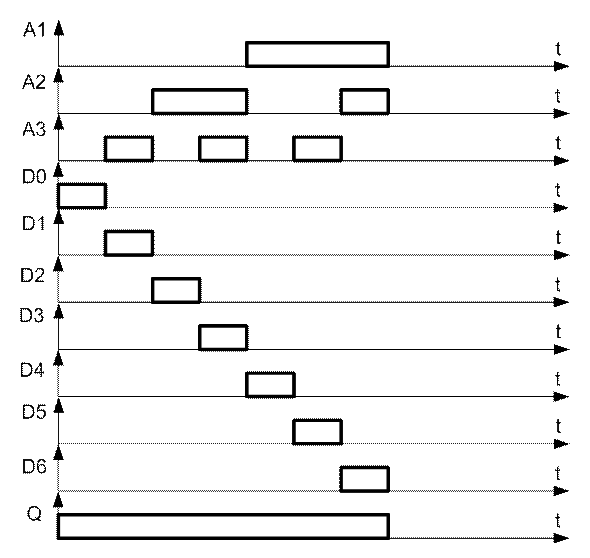
Рисунок 11 - временная диаграмма мультиплексора

7 Синтез регистров

Регистры представляют собой наборы триггеров со схемами управления.

Различают регистры памяти последовательные регистры, параллельно-последовательные.

В данном курсовом проекте будем рассматривать последовательный регистр или как его ещё называют сдвиговый. Такие регистры выполняют функцию сдвига информации влево или вправо. Ввод и вывод информации в сдвиговых регистрах осуществляется последовательно по разрядам, это достигается за счет последовательного подключения необходимого числа триггеров.

Построим сдвигающий регистр вправо на JK-триггерах. Для начала составим таблицу истинности по которой работает регистр (таблица 7). Примем, что на вход регистра поступает пятиразрядное двоичное число, тогда для построения регистра потребуется пять триггеров, соединенных последовательно. С неинверсных выходов каждого предыдущего триггера информация поступает на J-входы, а с инверсных – на К-входы каждого последующего триггера. Работа регистра управляется подачей синхроимпульсов с генератора импульсов на входы С триггеров. Обнуление происходит путем подачи на R-входы сигнала логической единицы от кнопки сброса, а на входе S постоянно присутствует высокий уровень логического сигнала для обеспечения работы триггеров в каждом такте.

Таблица 7 – Таблица истинности регистров

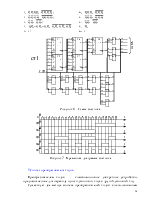
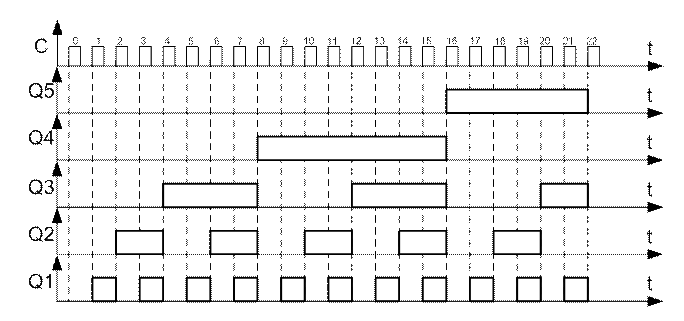
На рисунке 12 приведена схема регистра.

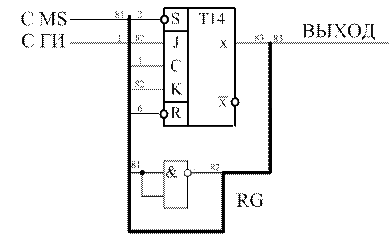
Рисунок 12 - Схема регистра RG

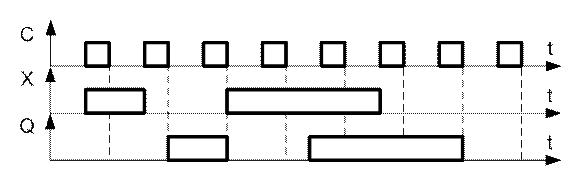
Рисунок 13 - Временная диаграмма регистра

8 Описание работы дискретного устройства

На принципиальной схеме дискретного устройства, выполненного на логических элементах ИЛИ-НЕ (микросхемы К155ЛЕ1, К155ЛЕ4 К155ЛЕ6 К155ЛЕ7) и D- триггерах (микросхемы 155ТМ2), используемых в качестве элементов памяти, показана реализация функциональных блоков этого