Построение логических устройств с жесткой логикой на базе современных интегральных схем

Сумматорами называют устройства, выполняющие арифметическую операцию сложения двоичных чисел по модулю два (Å).

Существует два вида сумматоров: с параллельным и последовательным действием. У сумматоров с параллельным действием сложение выполняется параллельно, сразу во всех разрядах суммируемых чисел. В сумматорах последовательным действием имеется только одна одноразрядная суммирующая схема и результат образуется последовательным сложением отдельных разрядов.

В курсовом проекте будет рассмотрен более подробно сумматор последовательного действия, построенного на полусумматорах. Составим таблицу истинности работы полусумматора (таблица 6)

Таблица 6 – ТИ полного одноразрядного сумматора

Входы		Выходы
а	b	S	P
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Запишем функции для суммы (S) и переноса (P) исходя из таблицы истинности и приведем их к необходимому базису.

На основе полученных формул построим схему сумматора в базисе И-НЕ, представленную на рисунке 8 и временную диаграмму (рисунок 9).

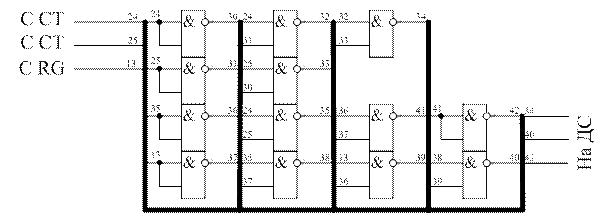
Рисунок 8– Схема сумматора по модулю два

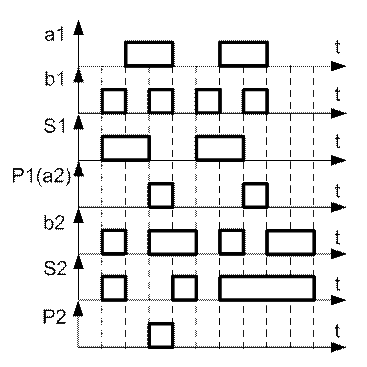
Рисунок 9– Временная диаграмма сумматора по модулю два

6 Синтез дешифратора

Дешифратор – комбинационное дискретное устройство, позволяющее получить на соответствующем десятичном выходе логическую единицу эквивалентную поданному входы двоичному коду.

Составим ТИ ДС (таблица 7). Затем получаем функции каждого выхода и строим принципиальную схему дешифратора и его временную диаграмму (рисунки 10 и 11 соответственно).

Таблица 7 – ТИ дешифратора

Входы			Выходы
Х3	Х2	Х1	Z
0	0	0	Z0
0	0	1	Z1
0	1	0	Z2
0	1	1	Z3
1	0	0	Z4
1	0	1	Z5

                                  

                           .

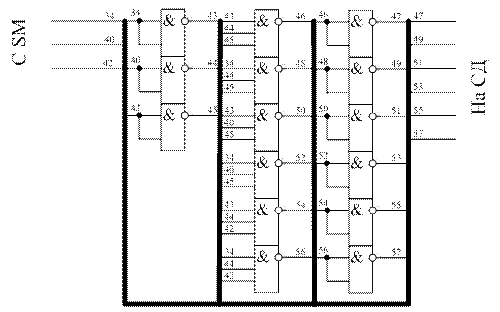
Рисунок 10 - схема дешифратора

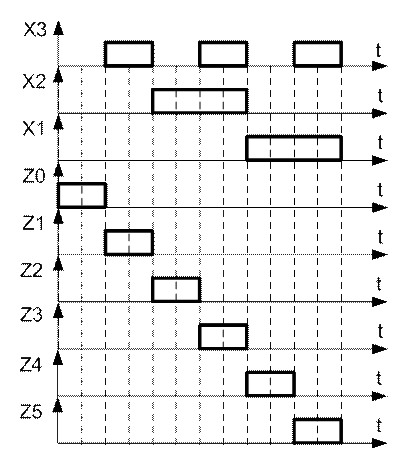
Рисунок 11 - временная диаграмма дешифратора

7 Синтез шифратора

Шифратор – комбинационное дискретное устройство, позволяющее получить на выходе кодовую комбинацию, соответствующую десятичному номеру входа, на котором появилась логическая единица.

Синтез шифратора может быть получен по его ТИ, в которой отражаются все возможные входы шифратора и все состояния выходов им соответствующие.

Составим ТИ СД для перевода десятичных цифр от 0 до 5 в код 3а+2 (таблица 8).

Таблица 8 – ТИ шифратора

Десятичная цифра	Код 3а+2
Xi	Y1	Y2	Y3	Y4	Y5
0	0	0	0	1	0
1	0	0	1	0	1
2	0	1	0	0	0
3	0	1	0	1	1
4	0	1	1	1	0
5	1	0	0	0	1

Запишем функции имеющие место с выходов дешифратора для функции Y2:

                                 

                                

Тогда функции выходов шифратора будут выглядеть следующим образом:

Разработаем шифратор, реализованный на базе асинхронных мультиплексоров (для функции Y2).

Разложим полученные функции по трем переменным предварительно составив таблицу разложения функций по трем переменным.

Х1	Х2	Х3	Значения функций Yi
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

В результате разложения получили две функции, для которых необходимо два отдельных мультиплексора, т. к. они состоят больше чем из одной переменной. Выполним их разложение по переменным Х4 и Х5:

Х4	Х5	Значение функции	Значение функции
0	0
0	1
1	0
1	1

Для остальных функций получим:

                                 

          

В результате получим схему (рисунок 12).

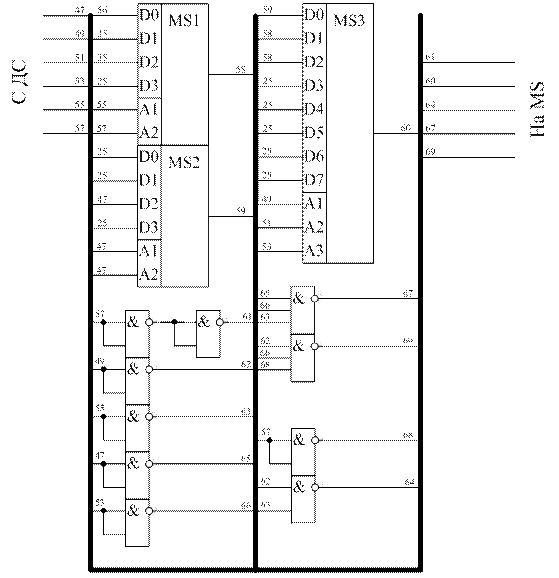
Рисунок 12 - Схема шифратора

Рисунок 13 - Временная диаграмма шифратора

8 Синтез мультиплексора

Мультиплексор – комбинационное дискретное устройство, которое подключает к выходу тот из входов данных, номер которого задан на адресных входах при наличии сигнала синхронизации.

Построим асинхронный мультиплексор с шестью входами данных, в качестве которых служат выходы с шифратора и один разряд счетчика (Т4), и тремя адресными входами, т. е. триггеры счетчика Т1, Т2, Т3. Для  этого необходимо составить таблицу истинности (таблица 9), на основании которой запишем логическое выражение для выхода Q,  и построим схему мультиплексора в базисе И-НЕ (рисунок 14).

Таблица 9 - таблица истинности мультиплексора

Таким образом получаем следующую принципиальную схему мультиплексора в базисе И-НЕ.

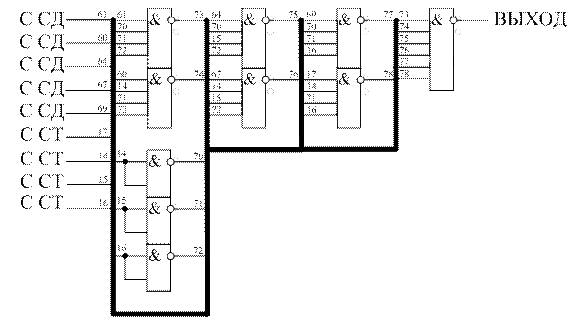
Рисунок 14 - Схема мультиплексора

Рисунок 15 - Временная диаграмма мультиплексора

9 Описание работы дискретного устройства

На принципиальной схеме дискретного устройства, выполненного