Передаточные функции и частотные характеристики активных фильтров
1 Краткие теоретические сведения
При каскадном соединении фильтров общую передаточную функцию фильтра представляют в виде произведения сомножителей W1,W2,…Wm,каждый из которых реализуется отдельным каскадом N1, N2,…Nm. Такой способ построения фильтров получил в настоящее время наибольшее распространение. Если звенья (каскады) такого фильтра не влияют друг на друга, то схема обладает требуемой передаточной функцией. Для реализации не взаимодействующих звеньев можно использовать ОУ, обладающие высоким Rвх и низким Rвых.
Для фильтров 1-го порядка передаточная функция представляется в виде:
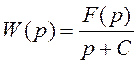 ,
,
где C – постоянное число, а F(p) – полином нулевой или первой степени.
Для фильтра 2-го порядка передаточная функция имеет вид:
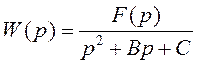 ,
,
где B и С – постоянные числа, а F(p) – полином второй или меньшей степени.
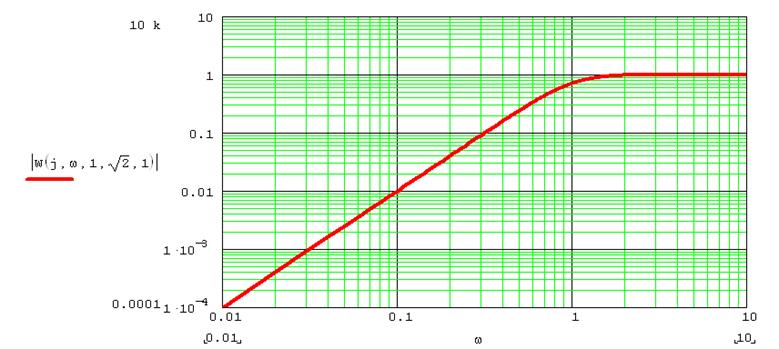
Амплитудно – частотная характеристика ФНЧ через коэффициент передачи:

|
|


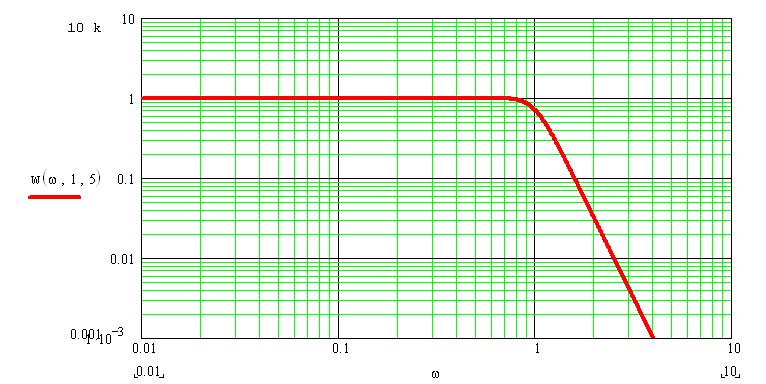
Для ФНЧ 2-го порядка с частотой среза ωc типовая полиномиальная передаточная функция имеет следующий вид:
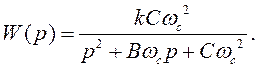
Постоянные В и С представляют собой нормированные числовые коэффициенты; постоянная k – коэффициент усиления.
Для фильтров более высокого порядка данное выражение описывает передаточную функцию типового звена 2-го порядка со своими коэффициентами B, C и k.
Фильтр верхних частот – частотно-избирательное устройство, пропускающее сигналы высоких частот и подавляющие сигналы низких частот. Характеристика ФВЧ может быть описана при помощи коэффициента передачи А(ω) или при помощи затухания α(ω) (для нормированной АЧХ):
![]()
![]() Примерная
амплитудно – частотная характеристика ФВЧ через коэффициент передачи имеет вид:
Примерная
амплитудно – частотная характеристика ФВЧ через коэффициент передачи имеет вид:
.

АЧХ ФВЧ
Типовая полиномиальная передаточная функция звена ФВЧ 2-го порядка получается из передаточной функции нормированного ФНЧ (имеющего ωс, равную 1 рад/с):
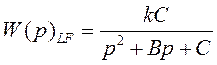 с
помощью преобразования:
с
помощью преобразования: 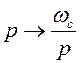
В результате получаем:
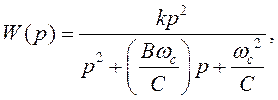
где k – коэффициент усиления ФВЧ (значение W(p) при p → ∞);
ωс – частота среза ФВЧ;
В и С – нормированные коэффициенты звена ФНЧ 2-го порядка.
Аналогично фильтру нижних частот, добротность определяется соотношением:
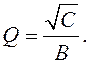
АЧХ ФВЧ определяется формулой:
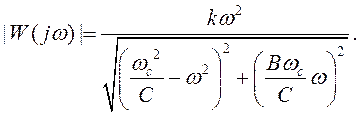
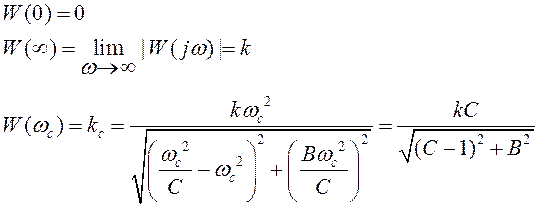
2 Схемы активных фильтров нижних частот
Вариант №1. ФНЧ на основе операционного усилителя (ОУ) с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления
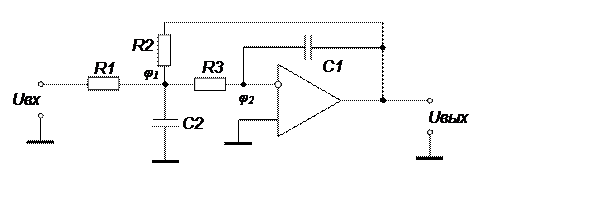 |
Передаточная функция фильтра
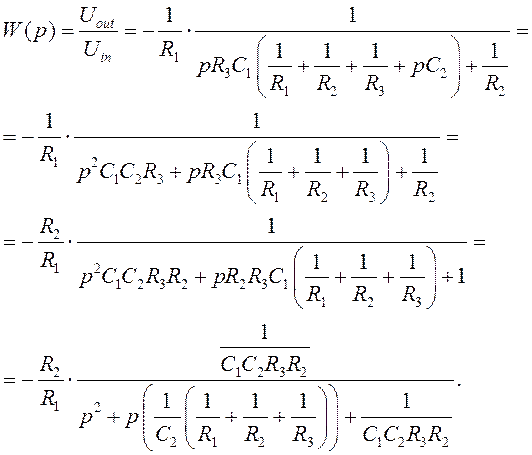
Из полученного выражения видно, что схема ФНЧ на ОУ с МОС реализует типовую полиномиальную передаточную функцию с инвертирующим коэффициентом усиления k, причем справедливы равенства:
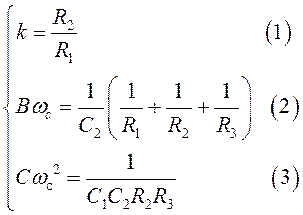
Если задаться значениями емкостей С1 и С2, то из данной системы можно найти значения сопротивлений R1, R2 и R3. Выведем формулы для расчета сопротивлений:
![]() из (1):
из (1):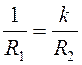
из (3): 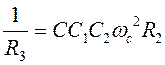
Подставляем эти значения в (2):
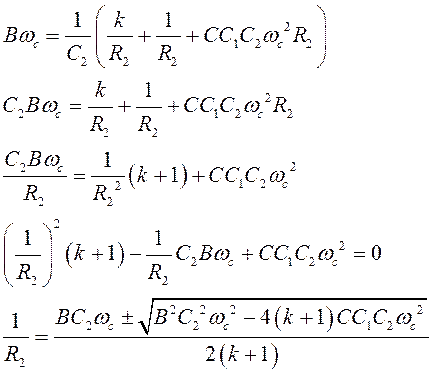
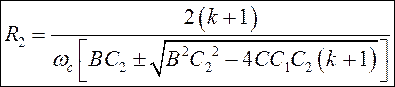
Для того, чтобы значение R2 было вещественным, необходимо ограничить значение С1:
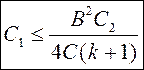
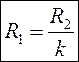
Вариант №2. ФНЧ на основе источника напряжения, управляемого напряжением
 |
Передаточная функция фильтра
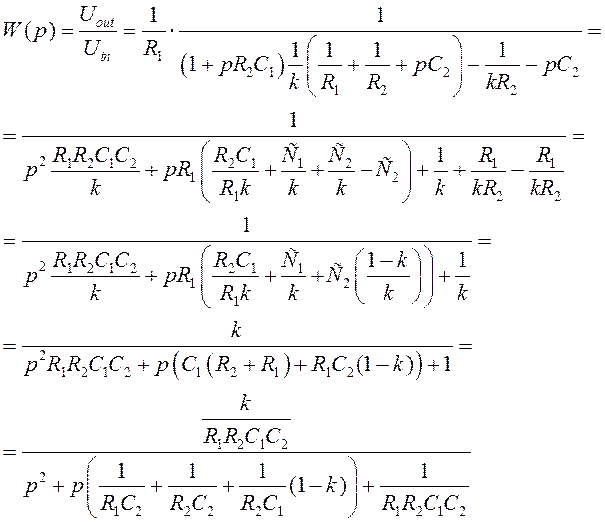
Из полученного выражения видно, что схема ФНЧ на ИНУН реализует типовую полиномиальную передаточную функцию с неинвертирующим коэффициентом усиления:
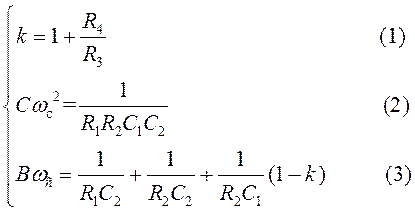
Из (2):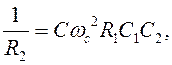 подставляем
в (3):
подставляем
в (3):
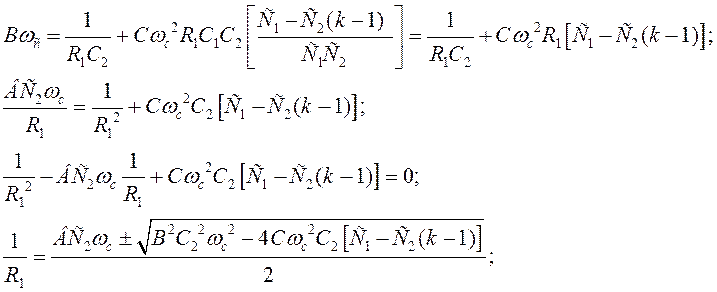
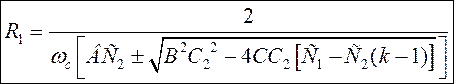
Для того, чтобы R1 было вещественным, ограничивается диапазон возможных значений С1:
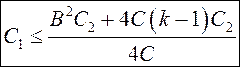
Из (2): 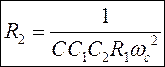
Значения R3 и R4 выбирается из условия минимизации смещения по постоянному току ОУ:
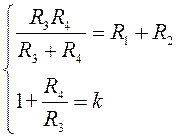
отсюда:
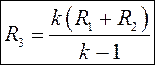
![]()
Вариант №3. ФНЧ на основе биквадратного звена
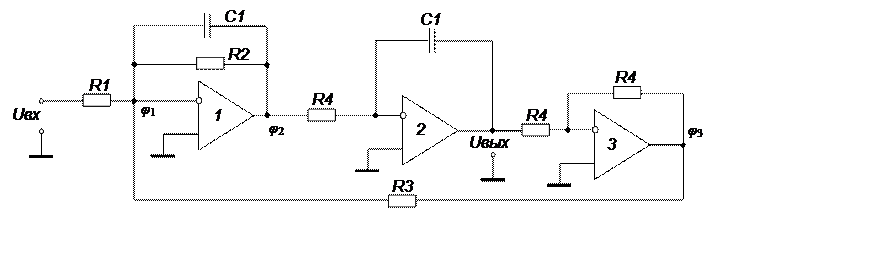
Передаточная функция фильтра
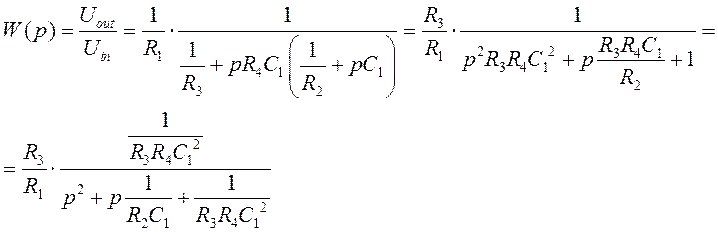
ФНЧ на основе биквадратной схемы реализует типовую полиномиальную передаточную функцию звена 2-го порядка с неинвертирующим коэффициентом усиления k, причем справедливо:
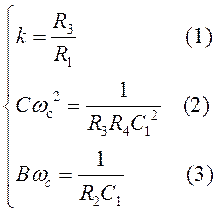
Из (2): 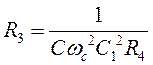
Из (3): 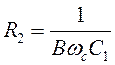
Из (1): 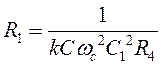
Значения С1 и R4 выбираются из условий:
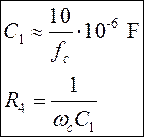
В этом случае получаем:
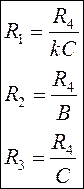
Из полученной системы видно, что биквадратная схема относительно легко настраивается. Для выбранных значений С1 и R4 изменение R2 приводит к изменению коэффициента В, изменение R3 – к изменению коэффициента С, а изменение R1– к изменению коэффициента усиления k.
Вариант №4. ФНЧ нечетного порядка
Для ФНЧ нечетного порядка одно из звеньев должно обладать передаточной функцией первого порядка:
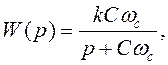
где k –коэффициент усиления звена, а C – нормированный коэффициент.
Указанную функцию реализует схема:
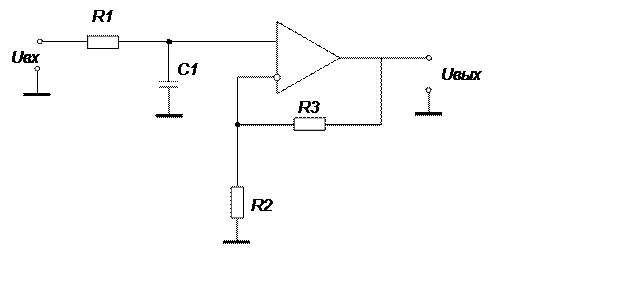 |
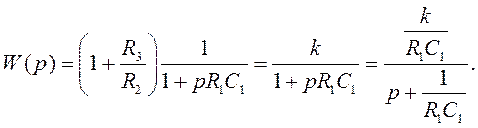
Отсюда запишем коэффициенты передаточной функции:
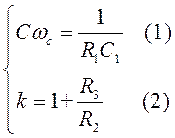
Из (1) получаем: 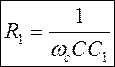
Значения сопротивлений R2 и R3 выбираются исходя из условия минимизации смещения ОУ по постоянному току:
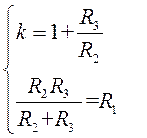
Отсюда получаем:
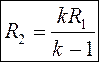
![]()
Схема легко настраивается: при выбранном значении С1 = 10/fc, мкФ, частота среза устанавливается резистором R1, а коэффициент усиления – отношением R3/R2. В случае k = 1 R3 заменяется короткозамкнутой цепью, а R2 – разомкнут.
Для данного звена необходимо обеспечить путь протекания постоянного тока на земляную шину с входа фильтра.
3 Схемы активных фильтров верхних частот
Вариант №5. ФВЧ на основе ОУ с многопетлевой обратной связью и бесконечным коэффициентом усиления
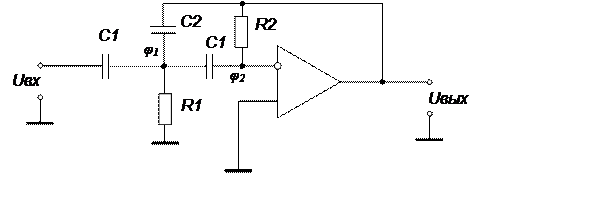 |
Передаточная функцию фильтра приведена ниже
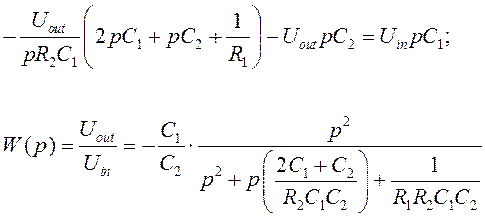
Из полученного выражения видно, что схема ФВЧ на ОУ с МОС реализует типовую передаточную функцию звена ФВЧ 2-го порядка с коэффициентами:
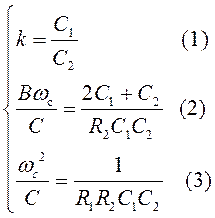
Если задаться значением емкости С1, то из (1) получим:
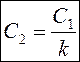
из (2): 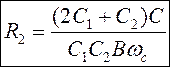
из (3): 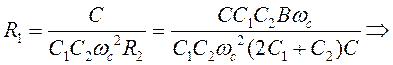
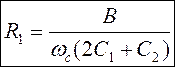
Вариант №6. ФВЧ на основе источника напряжения, управляемого напряжением
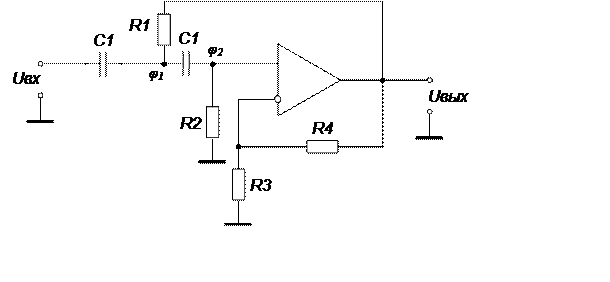 |
Передаточная функция фильтра:
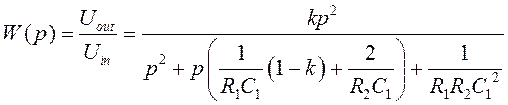
Отсюда запишем коэффициенты передаточной функции ФВЧ 2-го порядка:
![]()
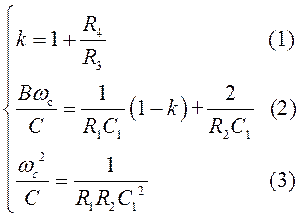
Если задаться значением С1, то из (3) получим:
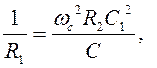 подставим в (2):
подставим в (2):
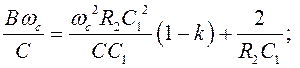 делим
обе части на R2
делим
обе части на R2
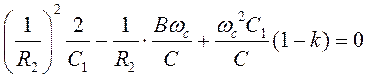
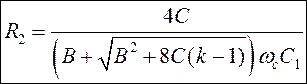
Из (3): 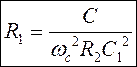
Номиналы R3 и R4 выбираются из условия минимизации смещения по постоянному току ОУ:
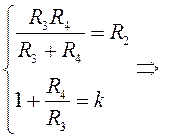
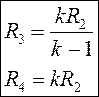
Вариант №7. ФВЧ нечетного порядка
Для ФВЧ нечетного порядка одно из звеньев должно обладать передаточной функцией первого порядка:
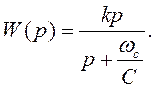
где k – коэффициент усиления звена при ![]() , а С – нормированный коэффициент
звена 1-го порядка ФНЧ-прототипа.
, а С – нормированный коэффициент
звена 1-го порядка ФНЧ-прототипа.
Указанную функцию реализует схема:
 |
![]()
Передаточная функция фильтра:
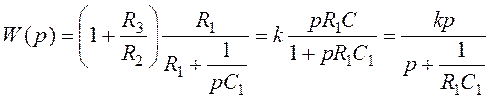 .
.
Для нахождения расчетных соотношений схемы решаем систему:
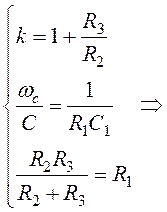
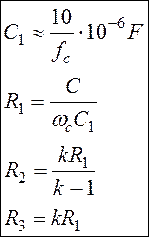
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.