Математическое моделирование линейных динамических стационарных систем и анализ их динамических и частотных характеристик в ППП Control System Toolbox СКМ Matlab

Лабораторная работа №11

Математическое моделирование линейных динамических стационарных систем и анализ их динамических и частотных характеристик в ППП ControlSystemToolboxСКМ Matlab

Цель работы: Ознакомление с динамическими и частотными характеристиками систем автоматического управления (САУ) и получение навыков интерактивного  исследования линейных динамических моделей.

1 Постановка задачи

В качестве объекта исследования выбраны линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов

.

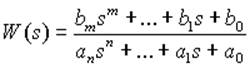Необходимо:

1. Определить полюса и нули передаточной функции

, .

2. Записать дифференциальное уравнение, определяющее функционирование САУ.
3. Построить графики переходной и импульсной характеристик:

h(t), w(t).

4. Построить логарифмические частотные характеристики

L (w ).

5. Построить частотный годограф Найквиста

W(iw ), w = [0, ¥ ].

       6. Построить карту нулей и полюсов передаточной функции (при выполнении анализа в режиме LTIVIEW).

2 Сведения по работе с ППП Control System Toolbox

2.1 Для выполнения лабораторной работы используется пакет прикладных программ (ППП) Control System Toolbox (CST). ППП предназначен для работы с LTI-моделями (Linear Time Invariant Models – линейными инвариантными моделями) технических систем и систем управления.

MatLab позволяет выполнить требуемый анализ несколькими способами:

- в интерактивном режиме, задавая команды ППП в командном режиме из Command Window ;

- в программном режиме, организовав m-файл или пользовательскийGUI-интерфейс;

- используя графический интерфейс ППП CST, который называется   LTI viewer;

- в режиме визуального моделирования пакета Simulink, создав файл моделирования Model.

Выбор способа анализа при решении прикладных инженерных задач моделирования определяется пользователем исходя из особенностей постановки задачи. При этом сложные и ответственные системы рекомендуется моделировать в различных режимах и сравнивать результаты моделирования.

В работе необходимо последовательно изучить и использовать все четыре указанные способа анализа.

В ППП Control System Toolbox имеется тип данных, определяющих динамическую систему в виде комплексной передаточной функции. Синтаксис команды tf, создающий в интерактивном режиме из Command Window LTI-систему с одним входом и одним выходом в виде передаточной функции:

>> W = tf([b_m, …, b₁, b₀], [a_n, …, a₁, a₀])

b_m, …, b₁ – значения коэффициентов полинома В числителя передаточной функции,

a_n, …, a₁ – значения коэффициентов полинома A знаменателя.

В результате в переменную W записывается LTI-система в виде передаточной функции. Коэффициенты можно разделять запятой или знаком пробела.

В окне вывода Workspace можно просмотреть созданную переменную.

Ниже показан пример создания двух LTI-систем с одинаковыми передаточными функциями, которые записаны в переменные W и H:

>> W = tf ( [1 3] , [5 7 1 2] )

Transfer function:

        s + 3

---------------------

5 s^3 + 7 s^2 + s + 2

>> H = tf ( [1,3] , [5,7,1,2] )

Transfer function:

        s + 3

---------------------

5 s^3 + 7 s^2 + s + 2

2.2 Интерактивный режим моделирования линейных динамических стационарных систем

Для выполнения работы необходимо использовать команды, приведенные в таблице 1.1.

Таблица 1.1. Основные команды ППП  Control System Toolbox

Синтаксис	Описание
pole(<LTI-объект>)	Вычисление полюсов передаточной функции
zero(<LTI-объект>)	Вычисление нулей передаточной функции
step(<LTI-объект>)	Построение графика переходной характеристики
impulse(<LTI-объект>)	Построение графика импульсной характеристики
bode(<LTI-объект>)	Построение логарифмических частотных характеристик (диаграммы Боде)
nyquist(<LTI-объект>)	Построение частотного годографа Найквиста

Пример применения команды step:

>> step(W)

Здесь W – передаточная функция технического объекта, созданная по команде tf.

Для определения корней полиномов степени k, может применяться команда MATLAB

roots(P),

которая, в качестве аргумента P получает матрицу коэффициентов полинома [p_k, …, p₀].

Приведённые выше команды могут быть организованы в программный фрагмент, записаны в m-файл и затем запускаться на выполнение, как программа.

2.3 Использование графического интерфейса ППП CST – LTI viewer

Использование графического интерфейса ППП CST – LTI viewer осуществляется вызовом команды из Command Window:

>> ltiview

В результате на экран дисплея будет выведено окно  LTI viewer.

Далее необходимо указать, какой LTI объект необходимо использовать для анализа: File ->  Import ->  W  -> OK